Лекция. Оператордың графигі және тұйықталған операторлар. Хан-Банах теоремасы және оның салдары
Өзі түйіндес операторды және тұйықтама операциясын әрі қарай зерттеу мақсатымен оператордың графигі ұғымын енгіземіз.
Гильберт кеңістігі 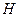 -тың екі данасын қарайық және
-тың екі данасын қарайық және  осы кеңістіктердің тура қосындысы болсын делік, яғни
осы кеңістіктердің тура қосындысы болсын делік, яғни 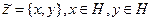 сызықтық операциялардың кәдімгі анықтамларымен анықталған қосақтар жиынтығы. Әрі қарай
сызықтық операциялардың кәдімгі анықтамларымен анықталған қосақтар жиынтығы. Әрі қарай  үшін осы элементтердің скаляр көбейтіндісін
үшін осы элементтердің скаляр көбейтіндісін  теңдігі көмегімен анықтаймыз. Скаляр көбейтіндінің барлық қасиеттері орындалатын тексеру қиын емес. Гильберт кеңістігінің қалған аксиомалары да түгел орындалады. Сондықтан,
теңдігі көмегімен анықтаймыз. Скаляр көбейтіндінің барлық қасиеттері орындалатын тексеру қиын емес. Гильберт кеңістігінің қалған аксиомалары да түгел орындалады. Сондықтан,  -та гильберт кеңістігі болады.
-та гильберт кеңістігі болады.
Егер H кеңістігінде сызықтық A операторы берілсе, онда 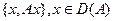 түріндегі элементтердің
түріндегі элементтердің  жақын, бұрынғыша, A операторының графигі деп атаймыз.
жақын, бұрынғыша, A операторының графигі деп атаймыз. 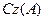 A операторымен бірмәнді анықталатын сызықтық көпбейне екенін оңай көруге болады. Керісінше егер A және B екі операторы үшін
A операторымен бірмәнді анықталатын сызықтық көпбейне екенін оңай көруге болады. Керісінше егер A және B екі операторы үшін 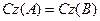 болса, онда A=B болады. Ең соңында A операторы тұйық болуы үшін
болса, онда A=B болады. Ең соңында A операторы тұйық болуы үшін 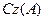 H кеңістігінің тұйық кеңістікасты болуы қажетті және жеткілікті екенін тексеру қиын емес.
H кеңістігінің тұйық кеңістікасты болуы қажетті және жеткілікті екенін тексеру қиын емес.  -та
-та 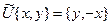 теңдігімен анықталатын
теңдігімен анықталатын  операторын қарайық.
операторын қарайық.
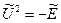 және
және 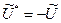 екeні түсінікті, содан
екeні түсінікті, содан  яғни
яғни  -унитар оператор
-унитар оператор
1-Лемма. Егер A бар жерде тығыз сызықтық D(A) көпбейнесінде анықталған кез-келген сызықтық оператор болса, онда  сызықтық
сызықтық  көпбейнесіне ортогонал толықтауыш болады.
көпбейнесіне ортогонал толықтауыш болады.
Дәлелдеме.  босын делік. Бұл <(
босын делік. Бұл <( 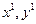 ),{
),{ 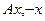 }> =0 екенін білдіреді. Бұдан
}> =0 екенін білдіреді. Бұдан 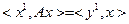 және , сондықтан,
және , сондықтан,  және
және  яғни
яғни 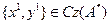 .
.
Пайымдауларды кері тәртіпте қайталап, 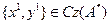 -тен осы элементтің
-тен осы элементтің  -дағы кез-келген элементке ортогонал екенін аламыз және лемме дәлелденді.
-дағы кез-келген элементке ортогонал екенін аламыз және лемме дәлелденді.
3-теoрема, Егер A H -та бар жерде тығыз D(A) жиынында анықталған тұйық оператор болса онда  -да бар жерде тығыз және
-да бар жерде тығыз және 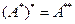 бірмәнді анықталған. Әрі
бірмәнді анықталған. Әрі 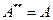 .
.
Дәлелдеме. A тұйық болатындықтан Cz(A) тұйық сызықтық көпбейне болады және, демек,  -да тұйық. Сондықтан
-да тұйық. Сондықтан
 /3/
/3/
Теңдіктің екі бөлігіне де унитар  операторын қолданып, және, біріншіден,
операторын қолданып, және, біріншіден, 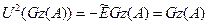 және, екіншіден, унитар операторортогонал элементтерді ортогонал элементтерге көшітінін ескере отырып
және, екіншіден, унитар операторортогонал элементтерді ортогонал элементтерге көшітінін ескере отырып
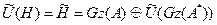 /4/
/4/
екенін аламыз.
Алдымен,  бар жерде тығыз екенін көрсетейік. Егер бұлай болмаса, онда
бар жерде тығыз екенін көрсетейік. Егер бұлай болмаса, онда  -ға ортогонал мүлдем ерекше,
-ға ортогонал мүлдем ерекше,  бар болады.
бар болады. 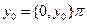 элементі
элементі 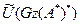 -ға ортогонал болады, себебі кез-келген
-ға ортогонал болады, себебі кез-келген 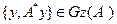 үшін
үшін
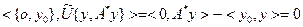
Сондақтан, 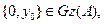 бұдан
бұдан 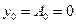 . Алынған қайшылық біздің ұйғарымымызды дәлелдейді.
. Алынған қайшылық біздің ұйғарымымызды дәлелдейді.
 бар жерде тығыз болғандықтан A** бірмәнді анықталады. A** =A теңдігін дәлелдеу үшін /4/ қатынасты және лемманы пайдалану жеткілікті.
бар жерде тығыз болғандықтан A** бірмәнді анықталады. A** =A теңдігін дәлелдеу үшін /4/ қатынасты және лемманы пайдалану жеткілікті.
4-теорема. A** операторы сонда, тек сонда ғана бар болады, егер бар жерде тығыз жиында анықталған A операторының тұйықтамасы болса. Бұл жағдайда A** =A.
Дәлелдеме. Егер A-ның 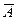 тұйықтамасы болса, онда 3-теорема бойынша
тұйықтамасы болса, онда 3-теорема бойынша  бар болады және
бар болады және  Бірақ
Бірақ 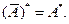 , сондықтан,
, сондықтан,  , бұдан A** =
, бұдан A** = 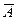 және теореманың I-бөлігі дәлелденді.
және теореманың I-бөлігі дәлелденді.
A** бар болсын делік. /3/-ті A*-ға қолданып, біз
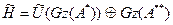 /5/
/5/
 екенін аламыз. Басқа жағынан,
екенін аламыз. Басқа жағынан,  операторын
операторын 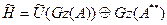 теңдігінің екі бөлігіне қолдана отырып
теңдігінің екі бөлігіне қолдана отырып

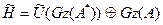
екенін аламыз. /5/ пен /6/-ны салыстырудан 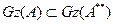 екені шығады, яғни А-ның тұйық кеңейтілуі
екені шығады, яғни А-ның тұйық кеңейтілуі 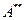 болады.
болады.
Шектеусіз операторлар үшін тағы инвариант кеңістікасты ұғымын енгізуге болады.
Егер
І/ 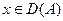 дан
дан 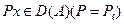 шықса,
шықса,
ІІ/ барлық  үшін
үшін  шықса/ яғни барлық
шықса/ яғни барлық 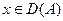 үшін
үшін  , онда L кеңістікасты A операторының инвариант кеңістікасты деп аталады.
, онда L кеңістікасты A операторының инвариант кеңістікасты деп аталады.
1/-ден және D(A)-ның H-та тығыздығынан  -де бар жерде тығыздығы шығады.
-де бар жерде тығыздығы шығады.
Шектеусіз симметриялы операторлар үшін L-дің инварианттылығынан  -дің инварианттылығы шығатынын көрсетейік. Іс жүзінде,
-дің инварианттылығы шығатынын көрсетейік. Іс жүзінде, 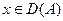 және
және 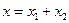 болсын делік, мұнда
болсын делік, мұнда  L- инвариант кеңістікасты болғандықтан
L- инвариант кеңістікасты болғандықтан 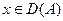 және D(A)-сызықтық көпбейне болғандықтан
және D(A)-сызықтық көпбейне болғандықтан 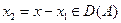 болады.
болады.
Әрі қарай, егер 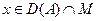 және y
және y  -деп кез-келген элемент болса, онда
-деп кез-келген элемент болса, онда  себебі
себебі 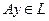 және
және  . Сонымен Ax элементі
. Сонымен Ax элементі  -ге ортогонал, ал бұл көпбейне L-де бар жерде тығыз болғандықтан
-ге ортогонал, ал бұл көпбейне L-де бар жерде тығыз болғандықтан 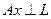 , бұдан
, бұдан  .
.
Егер L A операторының инвариант кеңістікасты болса, онда біз бұрынғыша L A-ны жетектейді /приводит/ дейміз.
5-теорема. L кеңістікасты симметриялық A операторын сонда, тек сонда ғана жетектейді, егер осы кеңістікасты үстіне проекциялайтын P операторы A-мен ауыстырымды болса.
Дәлелдеме. L-нвариант кеңістікасты болсын делік. Сонда, егер 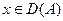 болса, онда
болса, онда 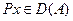 және
және  L-дің инварианттылығының 2/ шартынан
L-дің инварианттылығының 2/ шартынан
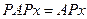 /7/
/7/
/7/ мен /8/ -ден 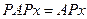 екені шығады және A-ның шектеулі P операторымен ауыстырымдылығы дәлелденді.
екені шығады және A-ның шектеулі P операторымен ауыстырымдылығы дәлелденді.
Керісінше, A мен P ауыстырымды болсын делік. Онда, ең алдымен 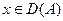 -дан
-дан 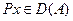 шығады.
шығады.
Әрі қарай,  үшін
үшін  , яғни
, яғни  және L-дің инварианттылығы дәлелденді.
және L-дің инварианттылығы дәлелденді.
Дата добавления: 2015-09-29; просмотров: 2566;
