Мысалдар.
1-мысал: R кеңістігінде ||x||=| arctgx | функциясы норма бола ма?
Шешуі:Норманың аксиомаларын тексерейік.
1) ||x||=|arctgx|³ 0 , егер ||x||=0 болса 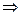 arctgx=0 , tg0=x
arctgx=0 , tg0=x 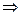 x=0; Керісінше, x=0 үшін arctgх=0 болады.Бұдан ||x||= arctgx=0
x=0; Керісінше, x=0 үшін arctgх=0 болады.Бұдан ||x||= arctgx=0 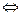 x=0 екені шығады.
x=0 екені шығады.
2)Екінші аксиоманы тексерейік. Шарт бойынша кез-келген aÎR саны үшін ||ax||=|arctgax|=|ax|| болуы керек. Бұл шарттың орындалмайтынын көрсету қиын емес. Мысалыға 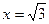 ,
, 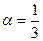 сандарын таңдап алсақ, онда
сандарын таңдап алсақ, онда
||ax||=|arctgax|=|arctg 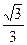 |=
|= 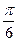
Бірақ, |ax||= 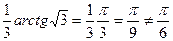 Þ ||ax|| ¹ |ax||
Þ ||ax|| ¹ |ax||
Екінші аксиома орындалмайды. Олай болса, ||x||=| arctgx | функциясы R кеңістігінде норма бола алмайды екен.
2-мысал: X=C[a,b]-кеңістігіне ( [a,b] кесіндісінде анықталған
үзіліссіз функциялар жиыны) тиісті функциялар үшін анықталған мына екі өрнек норма бола ма?
10. 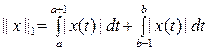 , мұндағы a < a+1 < b-1 < b ;
, мұндағы a < a+1 < b-1 < b ;
20. 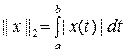 ;
;
Шешуі: Бұл сұраққа жауап беру үшін норманың үш аксиомасын зерттеу қажет.
10. Мұнда интеграл астындағы функция абсолют шамасымен қатысады, онда кез келген үзіліссіз x(t) функциясы үшін ||x||1³ 0 болады.
Егерде 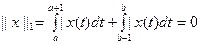 болса x(t)=0 бола ма ?
болса x(t)=0 бола ма ?
Бұл шарттың орынды болмайтынын көрсету қиын емес. Шынында x(t) функциясын мына түрде
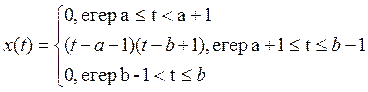
таңдап алсақ, онда x(t)Î C[a,b] , ||x||1=0 болады. Бірақ, x(t)¹0. Олай болса, норманың бірінші шарты, яғни ||x||1=0 Þ x(t)=0 орындалмайды.
Онда, C[a,b] кеңістігінде 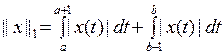 функциясы норма емес.
функциясы норма емес.
20. Мұнда да интеграл астындағы функция модулмен
берілгендіктен, кез келген үзіліссіз x(t) функциясы үшін ||x||2³ 0 болады.
Егер 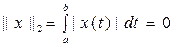 болса, онда x(t)=0 бола ма?
болса, онда x(t)=0 бола ма?
Мұнда интеграл астындағы функция оң таңбалы және үзіліссіз болғандықтан |x(t)|=0 болады. Бұдан x(t)=0 екені шығады және x(t)=0 функциясы үшін ||x||2=0 екені айқын. Бірінші аксиома толық орындалады.
Айталық, кез-келген 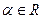 тұрақты сан берілген болсын , ол үшін норманың екінші аксиомасын тексерейік:
тұрақты сан берілген болсын , ол үшін норманың екінші аксиомасын тексерейік:
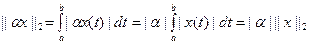
Екінші аксиома да орындалды.
Кез келген x(t), y(t) 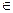 C[a,b] функцияларын алып, үшінші аксиоманы
C[a,b] функцияларын алып, үшінші аксиоманы
тексерейік.
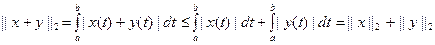
Демек, 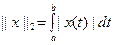 функциясы C[a,b] сызықтық кеңістігінде норма
функциясы C[a,b] сызықтық кеңістігінде норма
болады.
3-мысал: X=C1[a,b] - [a,b] кесіндісінде өзі және бірінші ретті туындысы үзіліссіз болатын функциялар жиынында
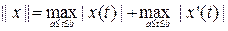
функциясы норма бола ма?
Шешуі:Норма шарттарын тексерейік.
1).||x||³ 0 екені айқын.
Егер
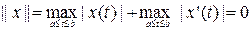
болса, онда 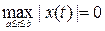 және
және 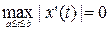
болуы керек. Егер қандай да бір y(t) - оң және үзіліссіз функциясын алып, оның a£ t£ b кесіндісіндегі максималды мәнін нөлге тең, яғни 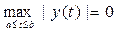 десек ,онда барлық tÎ [a,b] үшін y(t)º 0 болады. Бұдан барлық tÎ [a,b] үшін x(t)=0, x¢(t)=0 теңдіктері орынды екені келіп шығады. Олай болса, ||x||=0 шарты орынды болады. x(t)=0ÎC1[a,b] және ||0||=0 екені айқын.
десек ,онда барлық tÎ [a,b] үшін y(t)º 0 болады. Бұдан барлық tÎ [a,b] үшін x(t)=0, x¢(t)=0 теңдіктері орынды екені келіп шығады. Олай болса, ||x||=0 шарты орынды болады. x(t)=0ÎC1[a,b] және ||0||=0 екені айқын.
Ендеше, ||x||=0 Û x(t)=0.
2).Кез-келген aÎR нақты саны және x(t) 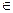 C1[a,b] үшін
C1[a,b] үшін
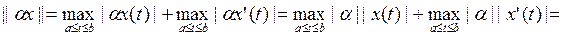
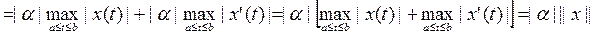
орынды болады.
Демек, ||a x||=|a| || x|.
3).x(t), y(t) 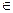 C1[a,b] берілген болсын. Онда
C1[a,b] берілген болсын. Онда
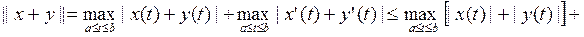
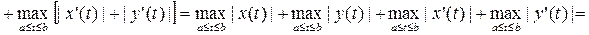
= ||x||+||y||
болады. Үшінші аксиома да орындалды.
Олай болса,
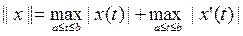
функциясы C1[a,b] кеңістігінде норма болады.
Дата добавления: 2015-09-29; просмотров: 2364;
