Лекция. Нормаланған кеңістіктер және оның мысалдары

Норма ұғымы бұл аналитикалық геометрия курсында үйренген векторлардың ұзындығы ұғымының жалпыламасы. Мұнда кез келген объектілерден тұратын, сызықтық кеңістік элементтері үшін норма ұғымы енгізіледі. Енді осы анықтаманы берейік:

1-анықтама:Егер Х сызықтық кеңістіктің кез-келген х 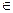Х элементі үшіноның нормасыдепаталатын || x ||функция анықталған болып:

1)|| x || ³ 0 - норма теріс болмаған сан,егер де||x||=0болсаÞх=q, керісінше х=q - нөлдік элементтің нормасы ||x|=0;

2)||ax||=|a|||x||,aÎR ;

3)"х,y 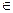Х элементтері үшін ||x+y||£||x||+||y|| (үшбұрыш теңсіздігі ) ;

аксиомалары орындалса, Х ті нормаланған кеңістікдеп атайды.

Егер Х сызықтық кеңістігінде норма анықталған болса, ол метрикалық кеңістікте болады. Мұнда нормаланған кеңістікке тиісті кез келген х,y элементтерінің ара-қашықтығы мына формуламен анықталады

,

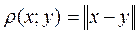яғни кез келген х , у 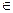Х үшін бұл функция метрика болады .

Шынында метриканың аксиомалары орынды болатынын тексерейік.

1) "x,y 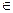Х үшін z= x-y деп белгілейік. Онда, норманың бірінші аксиомасы бойынша

||z||=||x-y|| ³ 0, егер ||z||=||x-y||=0 болса Û z=0, яғни x= y

Олай болса белгілеу бойынша

r( x,y) ³ 0, егер r( x,y)=0 болса Û x= y

Демек, метриканың бірінші аксиомасы орындалады.

2). "x,y 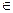Х үшін ||x-y||=||(-1)y+x||=||(-1)y- (-1)x||= |-1| || y- x||= ||y- x|| Þ.

r( x,y)= ||x-y||=||y-x||=r( y, x). Екінші аксиома да орындалды.

3). "x,y,z 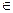Х үшін ||x-y||=||x-z+z-y||=||( x-z)+ (z-y)||£ || x-z||+ ||z-y|| Þ.

||x-y||=r( x,y) £ || x-z||+ ||z-y|| =r( x,z)+ r( z,y).

Метриканың үшінші аксиомасы да орындалды.

Сонымен, кез келген нормаланған кеңістік метрикалық кеңістік

болады.