Дискреттік программалау модельдері

Бульдік айнымалыларды пайдаланып шығарылатын тәжіри-беде жиі кездесетін маңызды есептердің бірі дискретті програм-малау есептері. Олар, есептеу объектісі және факторлары физи-калық түрде бөлінбейтін есептер. Ізделініп отырған айнымалылары тек бүтін мәндер қабылдайтын (мысалға, штаттық расписанияны жоспарлау және мәндері нөль немесе бір болатын логикалды немесе бульдік айнымалы жұмысқа тағайындау есептері) есептерді жатқызады. Сонымен, мұндай есептердің ерекшеліктері және екілік айнымалы есептерден айрықшылықтары былай түсіндіріледі: оңтайластырудың нәтижесінде оңтайлы мәндері ізделініп отырған айнымалылардың өзгеру аралығында кез келген үздіксіз мәндерінің бірі емес, тек олардың берілген нақты мәндерінің ішіндегі біреуі оңтайлы болуы мүмкін. Сондықтан мұндай сандар бүтін немесе бөлшек сандарда болады.

Дискретті программалау есептеріне бір мысал қарастырайық.

Мысал. Формасы параллелипипед болып келетін бактың сиымдылығы максимальды болатындай, табанының ені (a) және ұзындығы (b), сонымен қатар биіктігінің (h) ұзындықтарын табу керек.

Бак жасауға, ені: a = 4,25; 5,5 және 6,75 м, материалдарды қолдану ұсынылды. Материалдардың бағасы: С = kS =100 мың теңге, мұндағы k – 1 м² материалдың бағасы k =10 мың теңге, S – бак жасауға кеткен материал, м².

Есептің математикалық моделін құрамыз. Бактың көлемі:

V = abh, м³.

Бак жасауға керекті материалдың ауданы:

S = 2 (ab) + 2 (a +b)h = 2 (ab + (a + b)h), осыдан аламыз

С = kS =2 k(ab + (a + b)h).

Осындай әрекеттерден кейін есептің оңтайластыру моделін құрамыз:

V = abh → max

Берілген материалдардан жасалған максимальды сиымды бактың құны берілген бағадан (С_бер) көп болмауға тиіс:

2k (ab + (a + b)h) ≤ С_бер,

a, b, h ≥ 0 және a 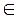4.25; 5.5; 6.75.

Есептің шарты бойынша бактың бағасы С_бер =100 және k = =10 мың теңге екенін ескерсек, онда бірінші теңсіздікті былай жазуға болады:

2∙10 (ab + (a + b)h) ≤ 100 немесе ab + (a + b) ≤ 5 (a)

Осыдан кейін бульдік айнымалылар арқылы математикалық модель мына түрде жазылады:

a = 4,25δ₁ + 5,5 δ₂ + 6,75 δ₃ немесе

a - 4,25δ₁ - 5,5 δ₂ - 6,75 δ₃ = 0 (б)

δ₁ + δ₂ + δ₃ =1 (в)

0 ≤ δ_j ≤ 1, j = 1, 2, 3.

δ_j – бүтін, j = 1, 2, 3.

Сонымен сызықты емес оңтайластыру моделі құрылды. Есепті MS Excel–де шығарамыз. Жұмыс бетіне барлық деректерді жазып, кестелік модель тұрғызамыз. Ол үшін B2:G2 аралықта мәндері ізделініп отырған (бульдіктермен қоса) айнымалылардың белгілері, E4:G4; E5:G5 және E6:G6 аралықтарда бульдік айнымалылардың төменгі және жоғары мәндері, сонымен қоса олардың бүтін сандар болу шарттары жазылды (2.14–сурет).

2.14-сурет

Жоғарыда сызықты емес программалау есебінің математи-калық моделі құрылғаны аталды. MS Excel көмегімен сызықты емес программалау есебін шығару тәсілінде сызықты програм-малау есебіне қарағанда мынадай өзгешеліктер бар:

– барлық ізделінетін айнымалыларға бастапқы мәндер тағайындалынады;

– Поиск решения–ның Параметры–де Линейная мо-дель–ді іске қосудың қажеті жоқ.

Бірінші талапты қамтамасыздандыру мақсатында B3:G3 аралыққа 1 жазамыз (2.14-сурет).

H9 ұяға мақсат функция формуласы: =B3*C3*D3, сонымен қатар H10, H11 және H12 ұяларында, сәйкесінше (а), (б) және (в) шектеулер формулаларының сол жағы: =B3*C3+(B3+C3);

=СУММПРОИЗВ (E11:G11;$E$3:$G$3) +B3 және

=СУММПРОИЗВ(E12:G12;$E$3:$G$3) жазылады.

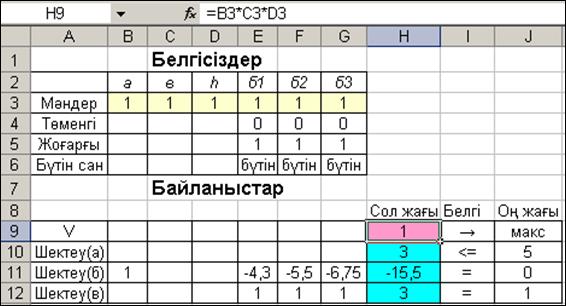
Поиск решения құралында мақсат функция ұясының адресін және бағытын, айнымалылар ұяларының аралығын және шектеулерді енгізгеннен кейінгі сұхбаттасу терезесінің бейнесі 2.15-суреттегідей болады.

2.15-сурет

2.16-сурет

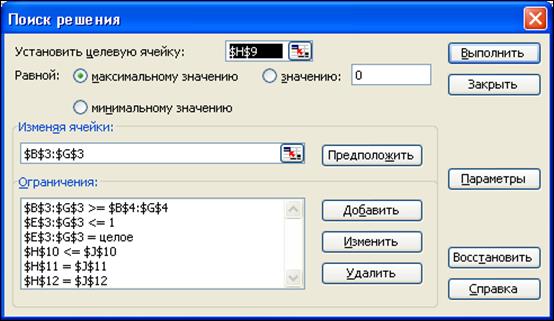
Сызықты емес программалау есебін шығару тәсілінің екінші талабы бойынша Парамер-дің сұхбаттасу терезесі 2.16-сурет-тегідей қалыпта қалады.

Выпонитьбатырмасын басқаннан кейін есептің шешімін аламыз (2.17-сурет).

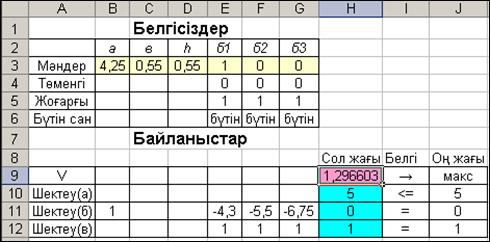
2.17-сурет

Алынған шешімнен параллелипипед формалы бактың а қабырғасы тең 4,25 м (a = 4,25 м), ал қалған қабырғаларының ұзындықтары бірдей және тең: b=h=0,55 м. Анықталған қабыр-ғаларының оңтайлы ұзындықтарында бактың сиымдылығы максимальды және тең: V= 1,2966 м³ .

Бактың а қабырғасының ұзындығы (4,25, 5,5 және 6,75 м) берілген және математикалық модельде олар туралы қосымша шектеулер қарастырылғандықтан, табылған бактың сиымдылығы, есепті қосымша шектеусіз шығарған сиымдықтан азаяды.

Сонымен, дискреттік программалау көмегімен алдын ала берілген мәндердің ішінен экстремальдық мәнге жетуге ықпал жасайтындай бір мәнді алуға болады, бірақ мұндай әдістен мақсат функция жақсармайды.

Дискретті программалау есептерін шығару барысында тек нәтиже бойынша есеп (Отчет по результатам) алынады. Онда ешқандай да жаңа деректер болмайды, сондықтан оны талдау қажетсіз. Нұсқалық талдау қалай жүргізілетініне тоқталсақ, олда сызықты емес программалау есептерінде қолданылған тәсілдер арқылы жүргізілетінін байқаймыз. Дискреттік программалау есеп-терін шығарғанда параметрлік талдау біраз қызықты. Мысалға, 2.18-суретте қарастырылып отырған есептің ізделіп отырған пара-метрлері (бактың қабырғаларының ұзындығы) үздіксіз (есепті бульдік айнымалыларысыз шешу) және үздікті (яғни дискретті программалау есебі құрылып, бірнеше мәндердің ішінен бір мәнді, бульдік айнымалылары арқылы таңдау) болған жағдайда нәтиже-лерді салыстырыу үшін сценария кестесі келтірілген.

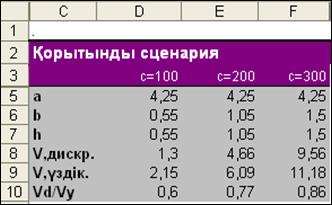
2.18-сурет

Ескерту: параметрлік талдауда жасалынған жұмыстар жоғарғы бөлімде жан-жақты баяндалуына байланысты, 2.18-суреттегі қорыттынды сценарияны қалыптастыру жолына терең тоқталмаймыз.

2.18-суретте келтірілген деректерден көріп отырмыз, алғаш-қы бағалары әртүлі бактардың көлемі, олардың параметрлері үздіксіз болған жағдайда дискреттік программалау талаптарымен анықтаған мәндерге қарағанда біраз жоғары. Бірақ, жобаланып отырған бактың бағасы өскен сайын, оның екі нұсқада есептелген максимальды сиымдылықтарының қатынасы бірге ұмтылатыны байқалады.

Сонымен, осындай және барлық шығарылатын есептер үшін де, жоғарыда келтірілген тәсілмен талдаулардың жасалуы, оңтайлы шешімдерді қабылдауда өте керекті пайдалы құрал екеніне айрықша көңіл аудару керектігін атап өтейік.