Раздельная оптимизация
Предположим, что многопродуктовая система включает N видов хранимой продукции, меду запасами которых отсутствует взаимодействие. Тогда общие издержки системы в единицу времени, связанные с размещением заказов и содержанием запасов N видов продукции составят:
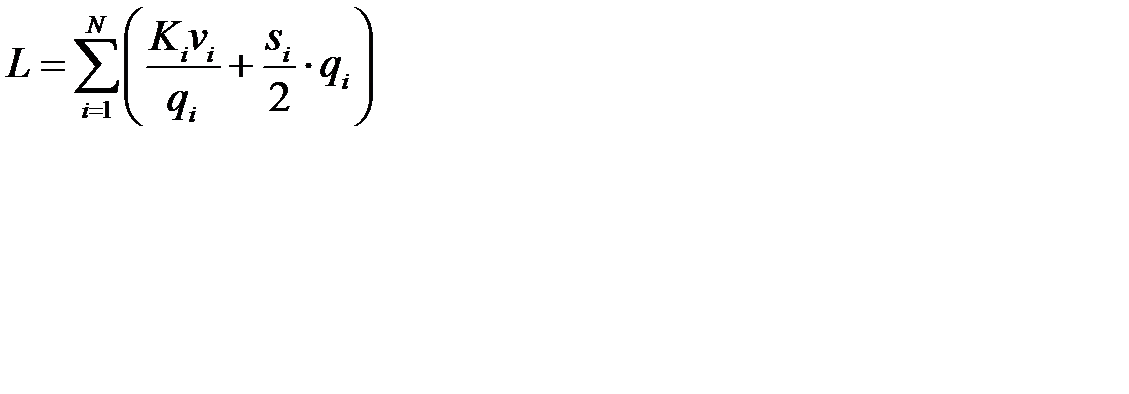 . (12.1)
. (12.1)
Издержки N видов продуктов являются функцией 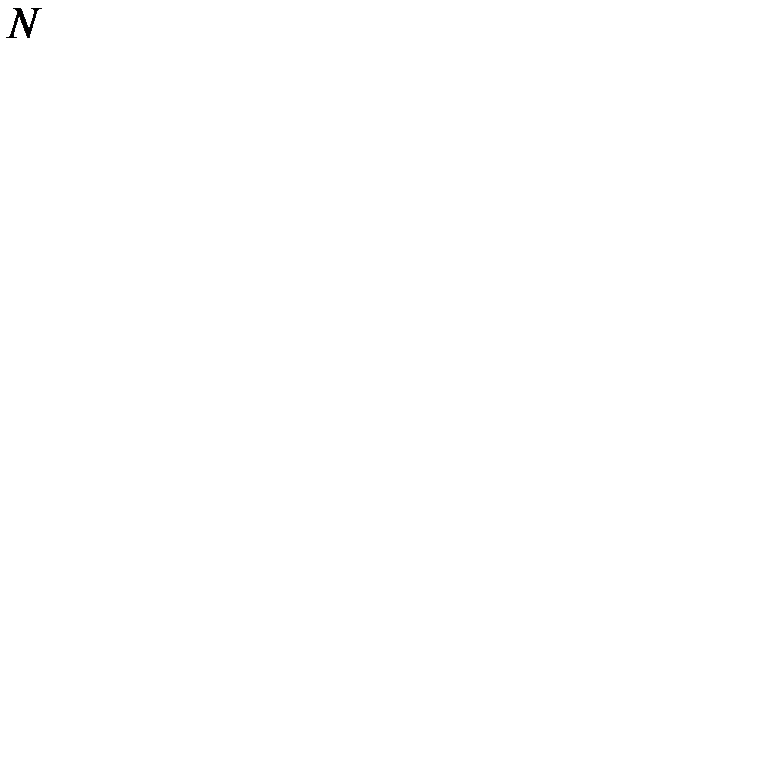 переменных:
переменных:  . Воспользуемся необходимым условием экстремума функции
. Воспользуемся необходимым условием экстремума функции  переменных. Для этого вычислим частные производные
переменных. Для этого вычислим частные производные  :
:
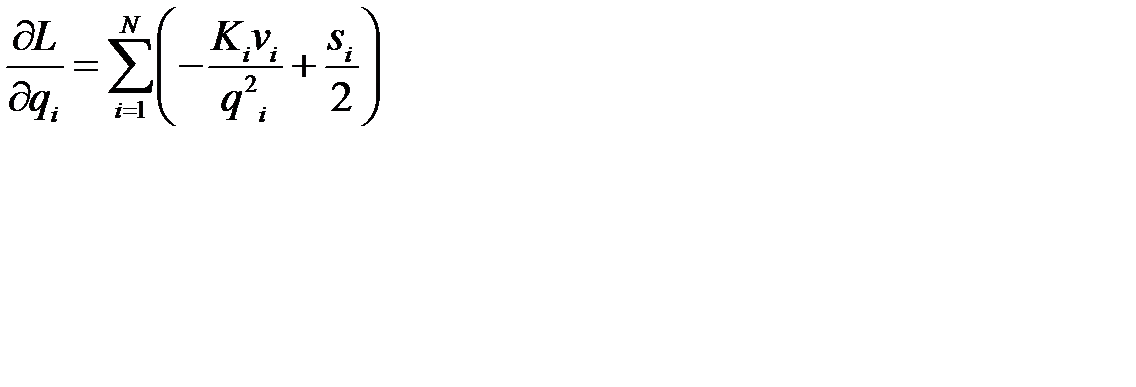 ,
,
приравняем их к нулю:
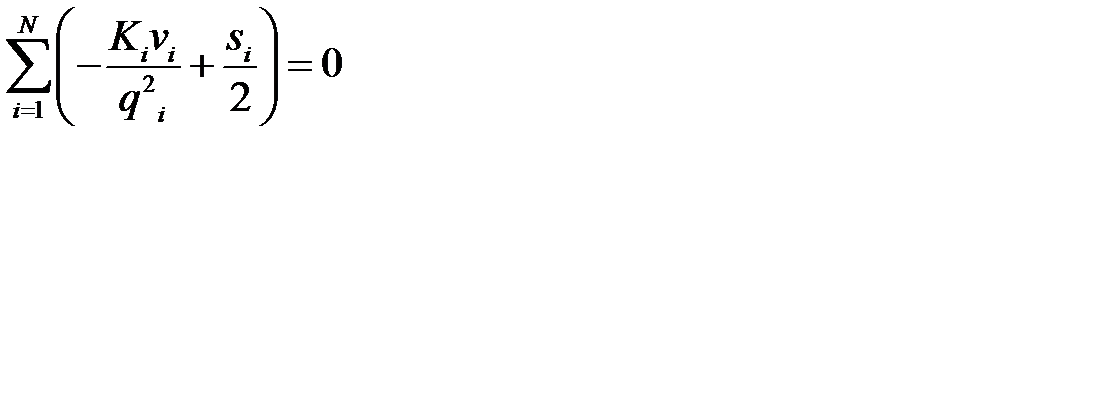
и найдем минимальные величины партий поставок 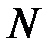 продуктов:
продуктов:
 ,
,  ; (12.2)
; (12.2)
длины циклов поставки 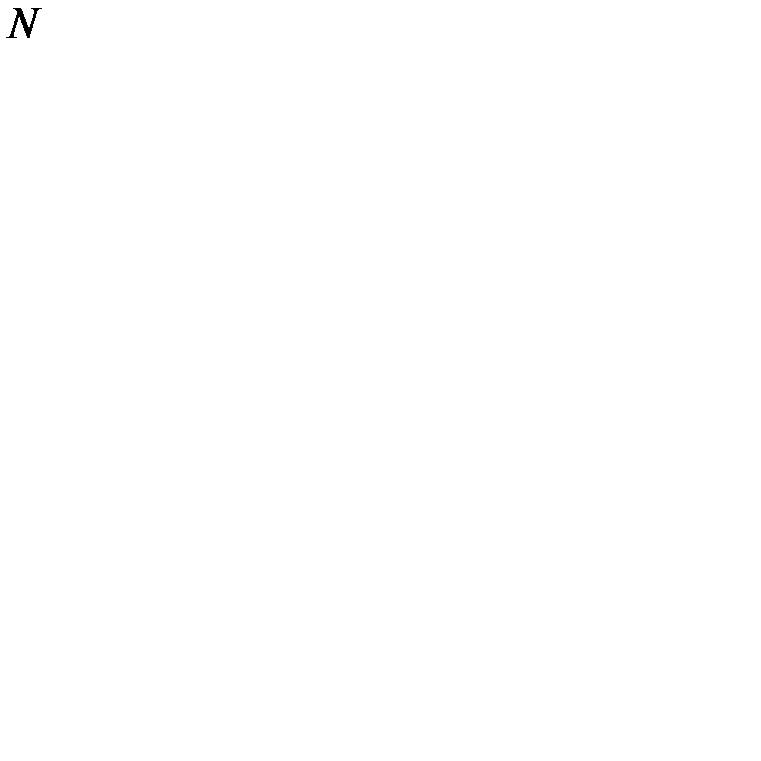 продуктов:
продуктов: 
Тогда минимальные издержки в единицу времени составят:
 .
.
Ограничения на складские площади. Предположим, что общая складская площадь ограничена величиной  , а единица продукции
, а единица продукции  го вида требует
го вида требует 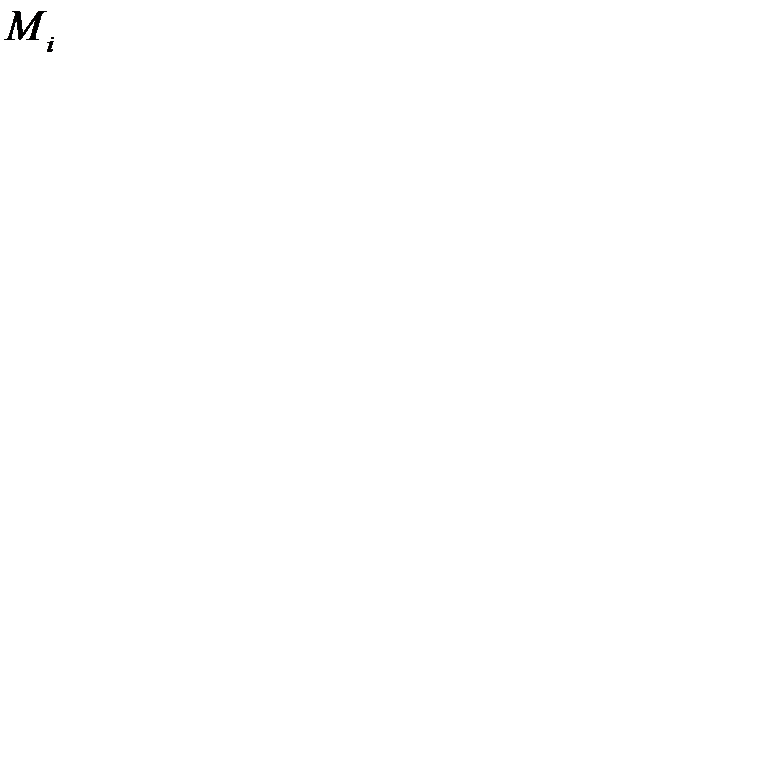 единиц складской площади. Обозначим через
единиц складской площади. Обозначим через  величину партии поставки продукции
величину партии поставки продукции  го вида. Тогда ограничение на складские площади примет вид:
го вида. Тогда ограничение на складские площади примет вид:  . Так как партии поставок поступают независимо друг от друга, то в левую часть неравенства следует ввести нормировочный множитель
. Так как партии поставок поступают независимо друг от друга, то в левую часть неравенства следует ввести нормировочный множитель  . Тогда получим неравенство
. Тогда получим неравенство
 . (12.3)
. (12.3)
Если  , то это значит, что запасы всех продуктов пополняются одновременно, и, следовательно, занятая ими площадь будет максимальной. Если
, то это значит, что запасы всех продуктов пополняются одновременно, и, следовательно, занятая ими площадь будет максимальной. Если 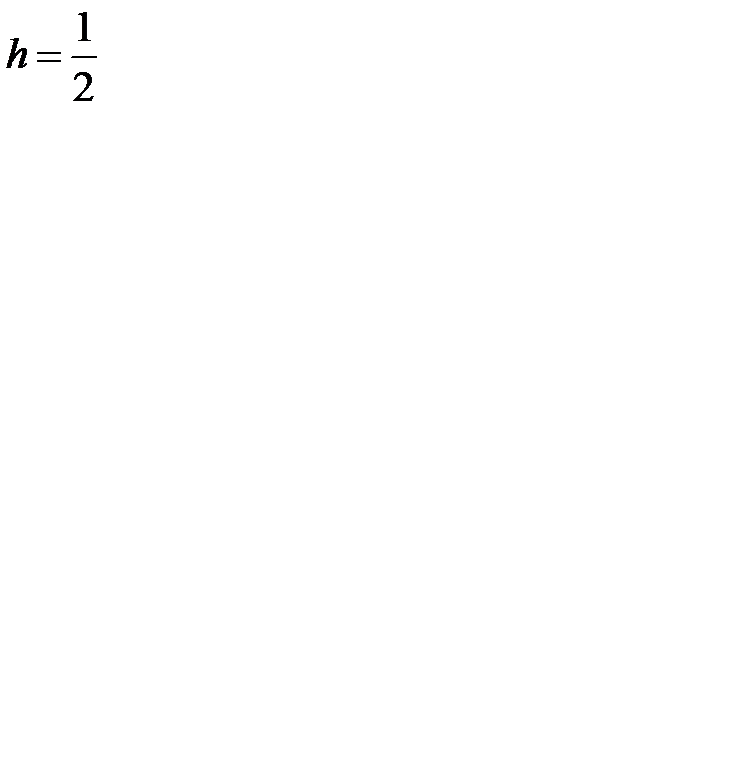 , то запасы всех видов продуктов пополняются в разное время, а уровень запасов и занятая ими площадь являются средними. Поскольку маловероятно, чтобы средний размер средств, вложенных в запасы, окажется меньше половины имеющейся площади, т. е. максимального уровня, то считают, что
, то запасы всех видов продуктов пополняются в разное время, а уровень запасов и занятая ими площадь являются средними. Поскольку маловероятно, чтобы средний размер средств, вложенных в запасы, окажется меньше половины имеющейся площади, т. е. максимального уровня, то считают, что 
Для нахождения экстремума функции издержек (12.1) при ограничениях (12.3) на складские площади воспользуемся методом нахождения условного экстремума. Составим функцию Лагранжа:
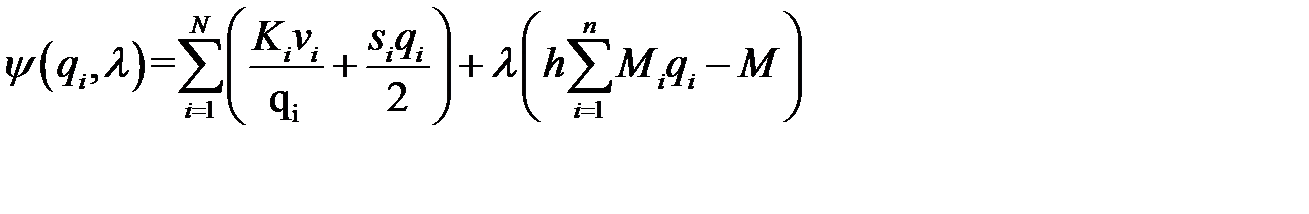 ,
,
где  - неопределенный множитель Лагранжа. Вычислим производные функции
- неопределенный множитель Лагранжа. Вычислим производные функции  по переменным
по переменным  и
и  :
:
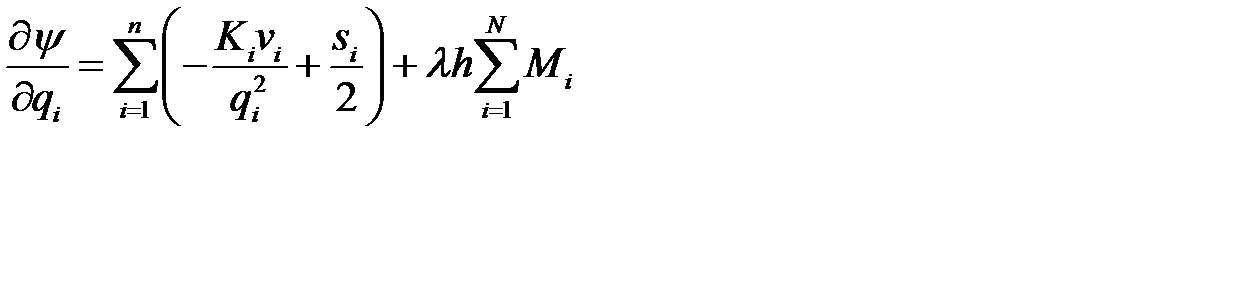 ,
,
 ,
,
приравняем их к нулю 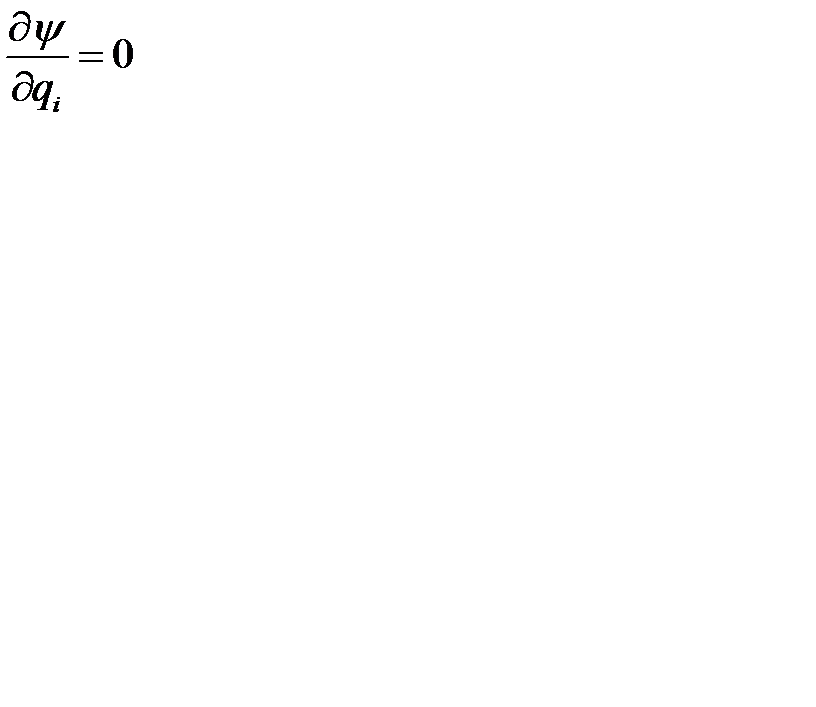 ,
,  и составим систему:
и составим систему:
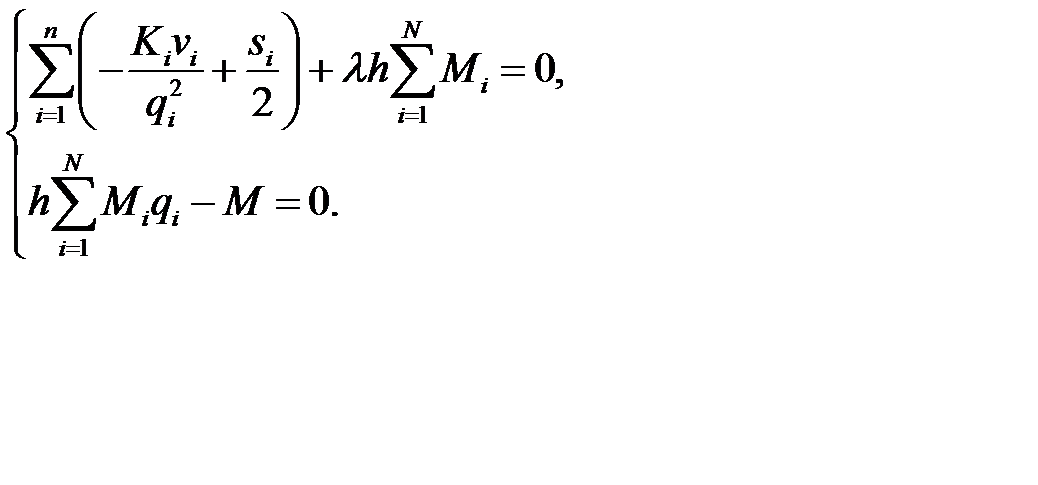
Преобразуем систему к виду:
 ,
,  ; (12.4)
; (12.4)
 (12.5)
(12.5)
Подставив значения  из (12.4) в (12.5), получим уравнение:
из (12.4) в (12.5), получим уравнение:
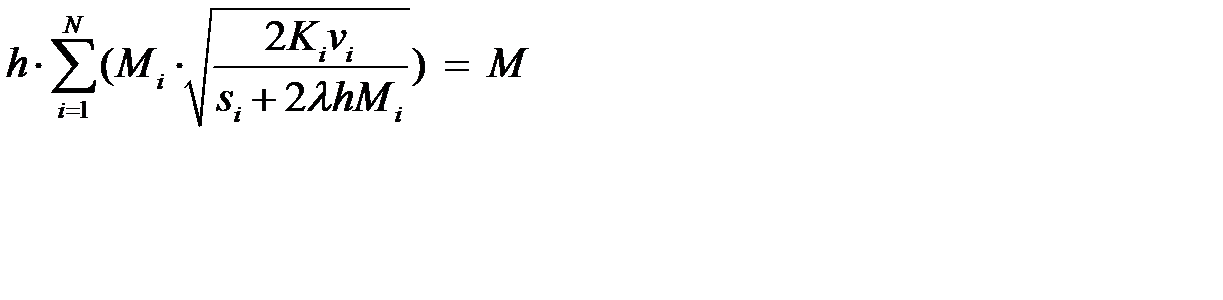 , (12.6)
, (12.6)
из которого находим значение  . Подставив найденное значение
. Подставив найденное значение  в (12.4) определяем оптимальные партии поставок
в (12.4) определяем оптимальные партии поставок  . Так как в выражении (12.4) знаменатели удовлетворяют неравенству
. Так как в выражении (12.4) знаменатели удовлетворяют неравенству  , то размеры оптимальных партий поставок уменьшаются при увеличении
, то размеры оптимальных партий поставок уменьшаются при увеличении  , что влечет увеличение издержек системы:
, что влечет увеличение издержек системы:
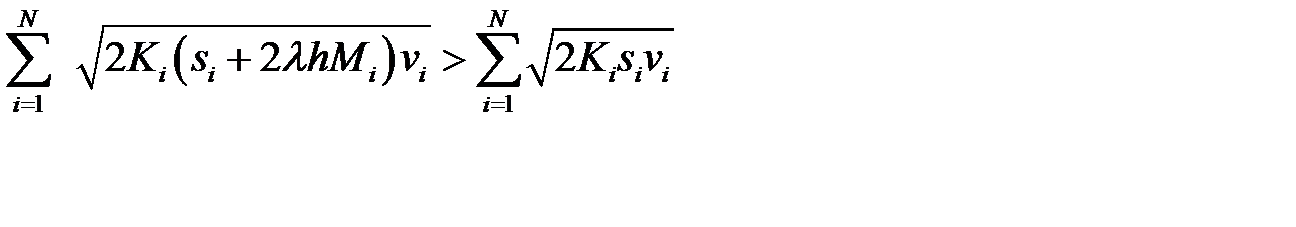 .
.
Это связано с тем, что вследствие уменьшения объема партии поставки растет их число в плановом периоде. Причем повышение издержек на размещение заказов превосходит их снижение от содержания запасов вследствие сокращения среднего уровня запасов.
Оптимальные партии поставок найдем, если определим  из (12.6). Множитель Лагранжа
из (12.6). Множитель Лагранжа  можно найти методом дихотомии, золотого сечения, Фибоначчи.
можно найти методом дихотомии, золотого сечения, Фибоначчи.
Определим экономическую интерпретацию множителя Лагранжа  . Для этого вычислим частную производную функции Лагранжа по
. Для этого вычислим частную производную функции Лагранжа по  . Частная производная равна
. Частная производная равна  , т.е.
, т.е.  (так как при вычислении частной производной по M все другие величины, считаются постоянными). Следовательно, приращение функции
(так как при вычислении частной производной по M все другие величины, считаются постоянными). Следовательно, приращение функции  приближенно равняется произведению производной на приращение аргумента
приближенно равняется произведению производной на приращение аргумента  , т.е.
, т.е.  . Поскольку функция
. Поскольку функция  определяет издержки в единицу времени, а М – площадь склада, то при
определяет издержки в единицу времени, а М – площадь склада, то при  получим
получим  . Следовательно, множитель Лагранжа
. Следовательно, множитель Лагранжа  показывает, на сколько можно сократить минимальные издержки системы в единицу времени, увеличив ограниченные складские площади на единицу площади.
показывает, на сколько можно сократить минимальные издержки системы в единицу времени, увеличив ограниченные складские площади на единицу площади.
Ограничения на величину оборотных средств. Аналогично решается задача, если ограничения накладываются на величину оборотных средств, вложенных в запасы. Если  – максимально допустимая величина оборотных средств, вложенных в запасы;
– максимально допустимая величина оборотных средств, вложенных в запасы;  – стоимость единицы
– стоимость единицы  -той продукции, то ограничение имеет вид:
-той продукции, то ограничение имеет вид:
 . (12.7)
. (12.7)
Составив функцию Лагранжа
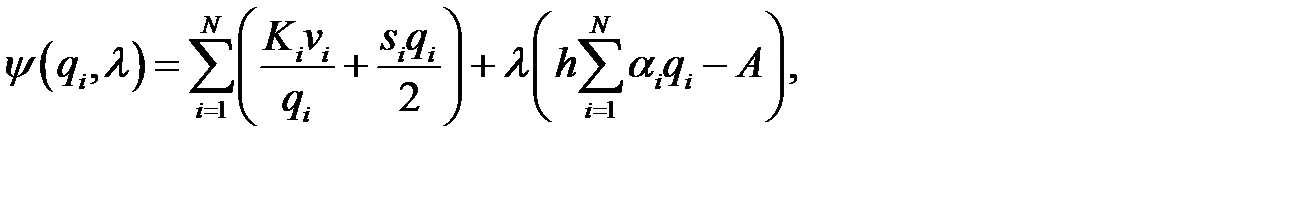
вычислив частные производные  и
и  , приравняв их к нулю
, приравняв их к нулю 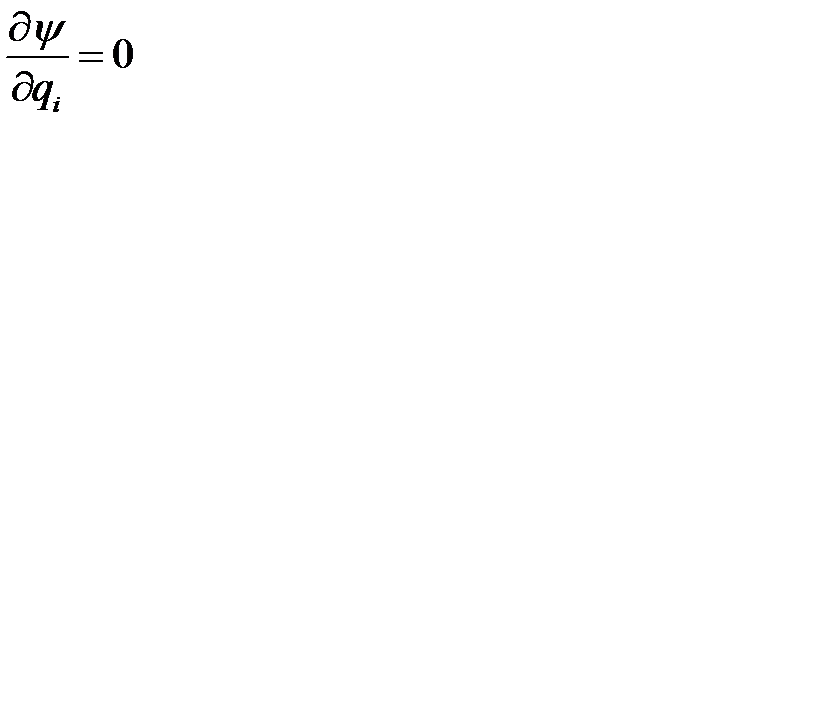 ,
,  , преобразуем полученную систему к виду:
, преобразуем полученную систему к виду:
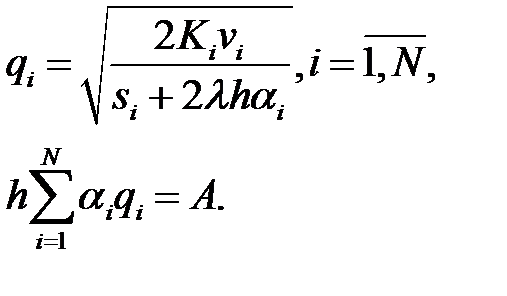
Неопределенный множитель Лагранжа  в этой модели, показывает на сколько денежных единиц уменьшаются затраты в системе, если оборотные средства увеличиваются на одну денежную единицу.
в этой модели, показывает на сколько денежных единиц уменьшаются затраты в системе, если оборотные средства увеличиваются на одну денежную единицу.
Если нужно найти минимальные издержки (12.1), при ограничениях на складские площади (12.3) и на оборотные средства (12.7), вложенные в запасы, то составляется функция Лагранжа вида:
 .
.
Вычислив частные производные функции  по переменным
по переменным  ,
,  и
и  , приравняв их к нулю, получаем систему:
, приравняв их к нулю, получаем систему:

решив которую, найдем оптимальную партию поставок. Поскольку решение системы достаточно сложно, то вначале можно поступить следующим образом. Определяем  по формуле (12.2) без учета ограничений и подставляем их в ограничения (12.3) и (12.7). Если неравенства выполняются, то ограничения несущественны и
по формуле (12.2) без учета ограничений и подставляем их в ограничения (12.3) и (12.7). Если неравенства выполняются, то ограничения несущественны и  является оптимальным. Если же хотя бы одно неравенство не выполняется, то решаем задачу при одном ограничении на площади или на оборотные средства. Полученные значения
является оптимальным. Если же хотя бы одно неравенство не выполняется, то решаем задачу при одном ограничении на площади или на оборотные средства. Полученные значения  , подставляем в другие ограничения и если они будут удовлетворять этому ограничению, то найденные значения
, подставляем в другие ограничения и если они будут удовлетворять этому ограничению, то найденные значения  будут оптимальными. Если же значения
будут оптимальными. Если же значения  не удовлетворяют другому ограничению, то решаем задачу вначале с этим ограничением и найденные значения
не удовлетворяют другому ограничению, то решаем задачу вначале с этим ограничением и найденные значения  подставляем в первое ограничение. Если и эти значения
подставляем в первое ограничение. Если и эти значения  не удовлетворяют ограничениям, то решаем задачу в общем случае.
не удовлетворяют ограничениям, то решаем задачу в общем случае.
Пример 12.1. В сборочный цех поступают комплектующие изделия пяти видов. Цех располагает складской площадью 260 м2. Данные о потребностях, издержках размещения заказов, издержках содержания запасов, расход площади на единицу комплекта представлены в таблице 12.1:
Таблица 12.1
Комплектующие, (  ) )
| Интенсивность потребления,  , (шт./год) , (шт./год)
| Издержки размещения заказа, 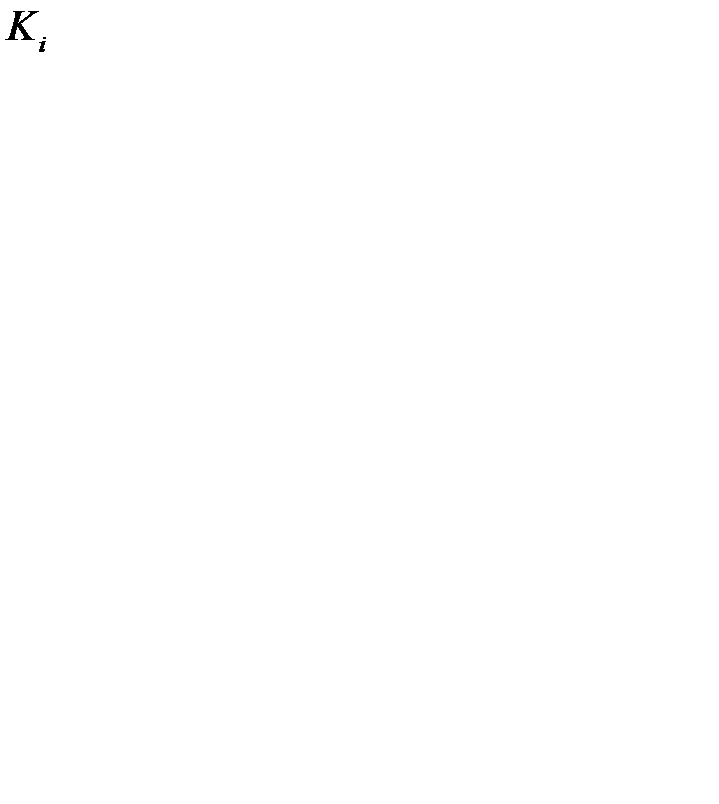 ,(ден. ед.) ,(ден. ед.)
| Расход площади 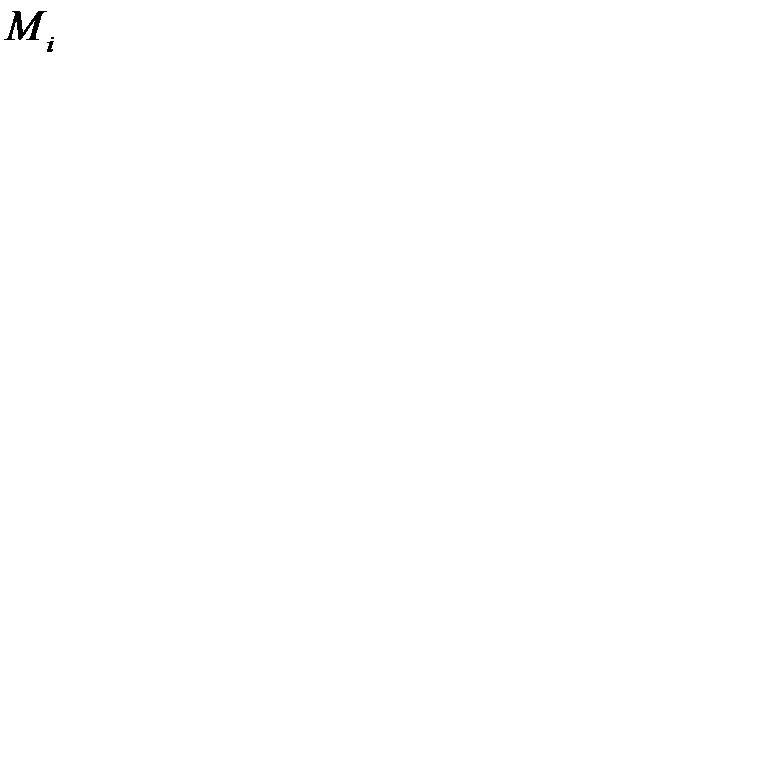 на одно комплектующее изделие (м2/шт.) на одно комплектующее изделие (м2/шт.)
| Издержки содержания в год, Si, (ден. ед.) |
| 1,5 |
Определить оптимальные партии поставок при ограничении на максимальный уровень запаса и издержки работы системы управления запасами с точностью до 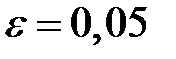 .
.
Решение. Если не учитывать ограничения на площадь, то оптимальные размеры поставок  на
на  -тый вид комплектующих определим по формуле Уилсона:
-тый вид комплектующих определим по формуле Уилсона:
 (шт.)
(шт.)  (шт.)
(шт.)  (шт.)
(шт.)  (шт.)
(шт.)
 (шт.)
(шт.)
Так как ограничение накладывается на максимальный уровень запаса, то проверим, выполняется ли неравенство (12.3) при  :
:
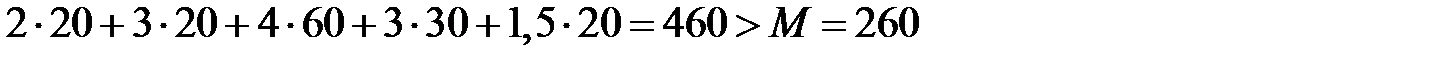 .
.
Из этого неравенства следует, что если запасы пополняются одновременно, то занятая ими площадь намного превышает существующую. Поэтому для нахождения  , удовлетворяющих ограничению (12.3) при h = 1, составим уравнение (12.6) относительно
, удовлетворяющих ограничению (12.3) при h = 1, составим уравнение (12.6) относительно  :
:
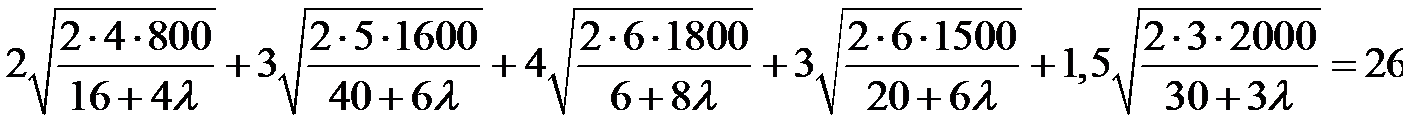
или
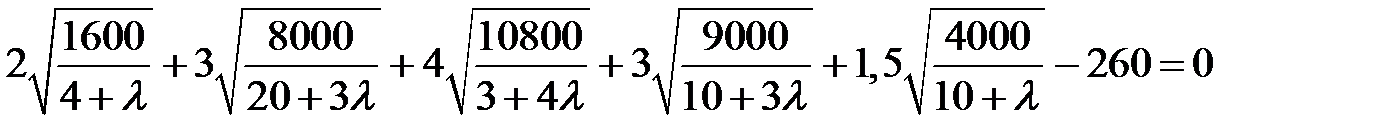 . (12.8)
. (12.8)
Для решения этого уравнения применим метод половинного деления отрезка. Подбор значений  и вычисление соответствующих значений
и вычисление соответствующих значений  сведем в таблицу 12.2, в последнем столбце которой будем записывать значение левой части уравнения (12.8).
сведем в таблицу 12.2, в последнем столбце которой будем записывать значение левой части уравнения (12.8).
Таблица 12.2

| 
| 
| 
| 
| 
| 
|
| 17,89 | 18,65 | 39,28 | 26,31 | 19,07 | 96,38 | |
| 16,33 | 17,54 | 31,33 | 23,72 | 18,26 | 49,15 | |
| 15,12 | 16,61 | 26,83 | 21,76 | 17,54 | 18,98 | |
| 14,14 | 15,81 | 23,84 | 20,23 | 16,90 | -2,89 | |
| 3,5 | 14,61 | 16,20 | 25,21 | 20,95 | 17,21 | 7,325 |
| 3,75 | 14,37 | 16,00 | 24,49 | 20,58 | 17,06 | 3,875 |
| 3,875 | 14,25 | 15,90 | 24,16 | 20,40 | 16,98 | -0,49 |
| 3,85 | 14,28 | 15,92 | 24,23 | 20,44 | 16,99 | 0,045 |
Метод половинного деления отрезка основан на следующей теореме дифференциального исчисления: «Если функция f(x) непрерывна на отрезке [a,b] и на концах отрезка принимает значения разных знаков (  ), то на этом отрезке существует точка
), то на этом отрезке существует точка  , в которой функция обращается в нуль, т.е.
, в которой функция обращается в нуль, т.е.  .»
.»
Если  возрастает, то левая часть уравнения (12.8) является монотонно убывающей функцией. Поэтому, существует только одно значение
возрастает, то левая часть уравнения (12.8) является монотонно убывающей функцией. Поэтому, существует только одно значение  , при котором функция обращается в нуль, и это значение
, при котором функция обращается в нуль, и это значение  будет корнем уравнения.
будет корнем уравнения.
Для нахождения значения  воспользуемся сформулированной теоремой.
воспользуемся сформулированной теоремой.
Придавая значения  , мы находим отрезок, на котором функция
, мы находим отрезок, на котором функция 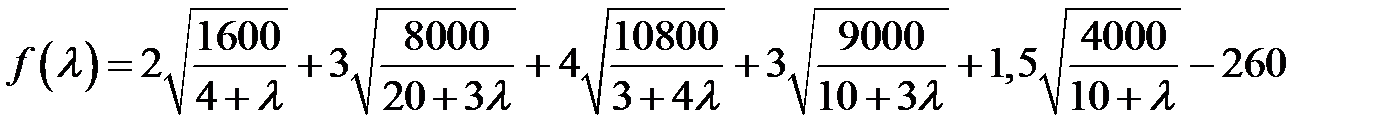 принимает значения разных знаков. Это будет обозначать, что на этом отрезке существует значение
принимает значения разных знаков. Это будет обозначать, что на этом отрезке существует значение  , в котором функция
, в котором функция  обращается в нуль. Следующим значением
обращается в нуль. Следующим значением  будет середина этого отрезка
будет середина этого отрезка  . Из двух полученных отрезков
. Из двух полученных отрезков  и
и  выбираем тот, на концах которого функция
выбираем тот, на концах которого функция  имеет разные знаки. Снова находим его середину и т.д. Процесс деления отрезка продолжается до тех пор, пока не будет выполнена заданная точность, т.е. значение функции
имеет разные знаки. Снова находим его середину и т.д. Процесс деления отрезка продолжается до тех пор, пока не будет выполнена заданная точность, т.е. значение функции  .
.
Если  =0, то
=0, то  и значения
и значения  вычисляем по формуле Уилсона. Если
вычисляем по формуле Уилсона. Если  , то
, то  ,
,  ,
,  ,
,  ,
,  ;
;
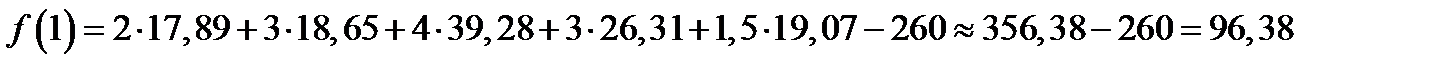 .
.
Если  =2, то
=2, то
 ,
,  ,
,  ,
,  ,
,  ;
;
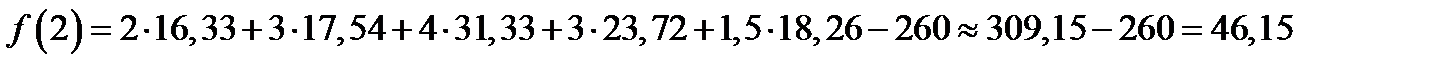 .
.
Если  =3,то
=3,то
 ,
,  ,
,  ,
,  ,
,  ;
;
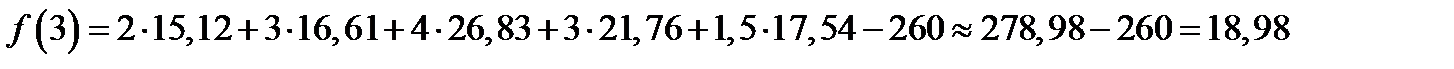
Если  =4,то
=4,то
 ;
;  ,
,  ;
;  ;
;  ;
;
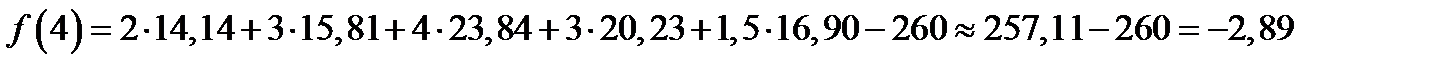 .
.
Итак, на отрезке [3;4] функция  принимает значения разных знаков. Следовательно, корень уравнения (12.8) находится на этом отрезке.
принимает значения разных знаков. Следовательно, корень уравнения (12.8) находится на этом отрезке.
Следующее значение  равно середине этого отрезка -
равно середине этого отрезка -  . Тогда
. Тогда
 ;
;  ;
;  ;
;  ;
;  ;
;
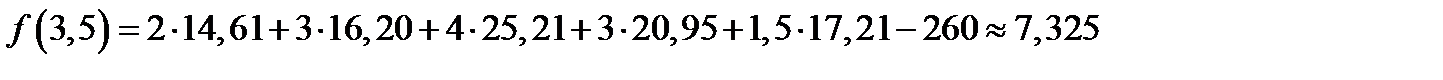
Так как  , то корень уравнения (12.8) находится на отрезке [3,5;4]. Положим
, то корень уравнения (12.8) находится на отрезке [3,5;4]. Положим  . Тогда
. Тогда
 ;
;  ;
;  ;
;  ;
;  ;
;
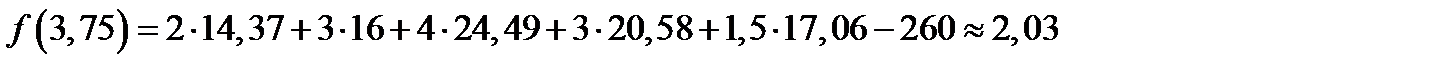
Положим  . Тогда
. Тогда
 ;
;  ;
;  ;
;  ;
;  ;
; 
Так как  , то корень находится на отрезке [3,75; 3,875]. Заданная точность будет выполнена, если положим
, то корень находится на отрезке [3,75; 3,875]. Заданная точность будет выполнена, если положим  :
:
 ;
;  ;
;  ;
;  ;
;  ;
;

Если бы не было ограничений на складские площади, то среднегодовые затраты составили бы:
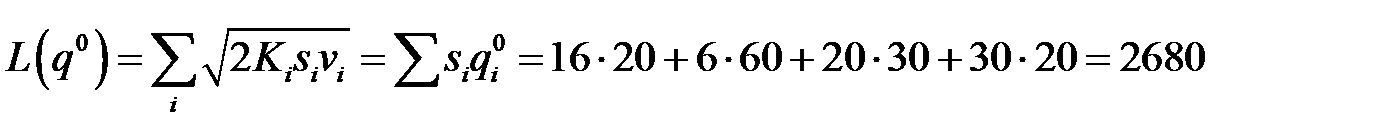 (ден.ед. в год). При ограничениях среднегодовые издержки равны:
(ден.ед. в год). При ограничениях среднегодовые издержки равны:
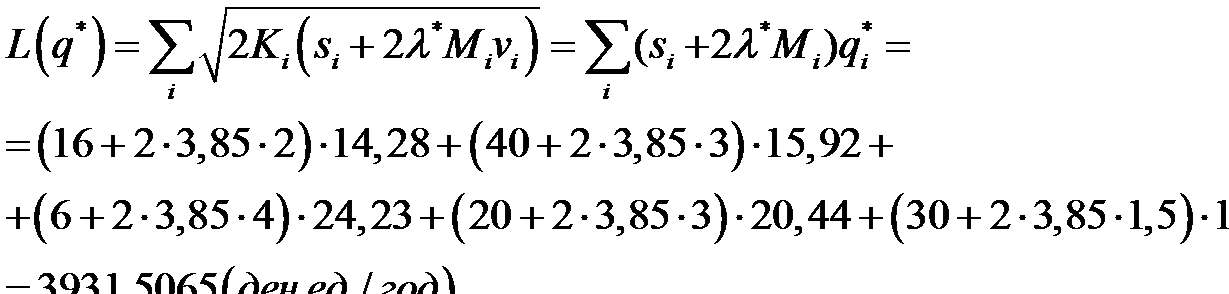
Дата добавления: 2015-09-29; просмотров: 1357;
