Модель в условиях скидки на размер заказа
Для увеличения объема продажи фирмы предлагают количественные скидки, т.е. снижение цены при оптовых закупках. Скидка может быть оптовой и дифференциальной.
Рассмотрим случай оптовой скидки, когда с увеличением размера заказываемой партии  уменьшается стоимость каждой единицы товара. Предположим, что величина заказываемой партии может быть либо
уменьшается стоимость каждой единицы товара. Предположим, что величина заказываемой партии может быть либо  , либо
, либо  , где
, где  некоторый объем продукции. При
некоторый объем продукции. При  стоимость единицы продукции равна
стоимость единицы продукции равна  , а при
, а при  стоимость единицы продукции равна
стоимость единицы продукции равна  , причем
, причем  .
.
При  издержки работы системы в течение цикла состоят из:
издержки работы системы в течение цикла состоят из:
- издержек размещения заказа 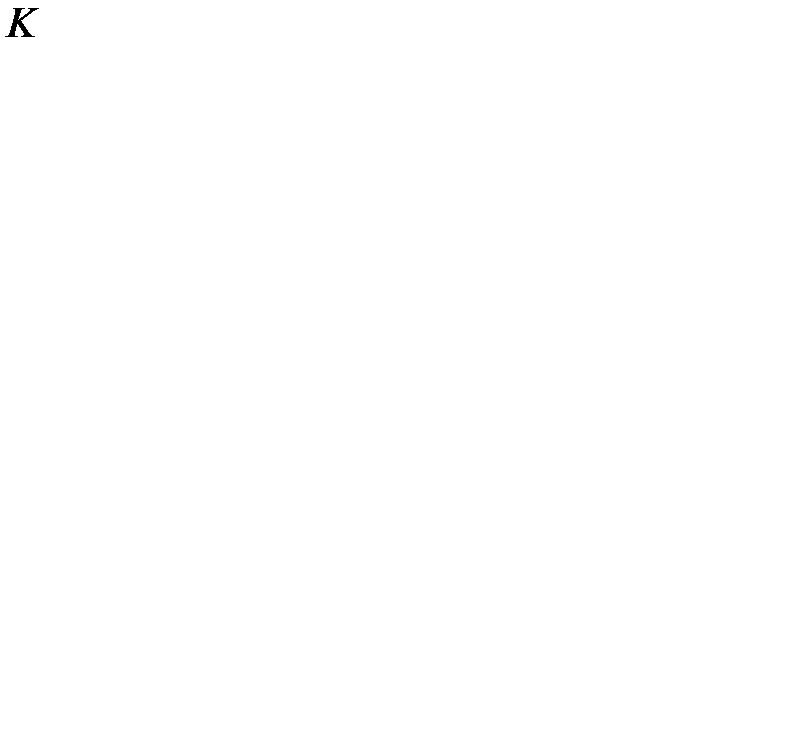 ;
;
- издержек содержания  единицы заказа в единицу времени, как процент от стоимости единицы продукции
единицы заказа в единицу времени, как процент от стоимости единицы продукции  , где
, где  – стоимость содержания, выраженная в процентах от стоимости единицы продукции
– стоимость содержания, выраженная в процентах от стоимости единицы продукции  ;
;
- стоимости единицы продукции  партии
партии  :
:
 .
.
Разделив издержки на длину цикла, получим издержки в единицу времени:
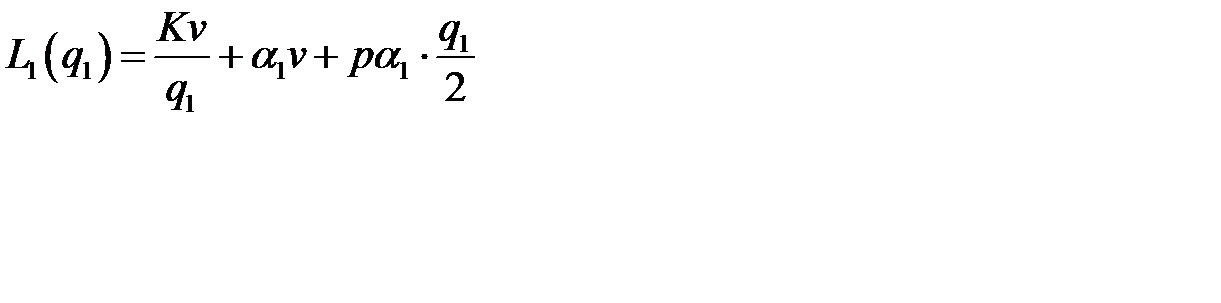 .
.
Аналогично, при  издержки в единицу времени равны:
издержки в единицу времени равны:
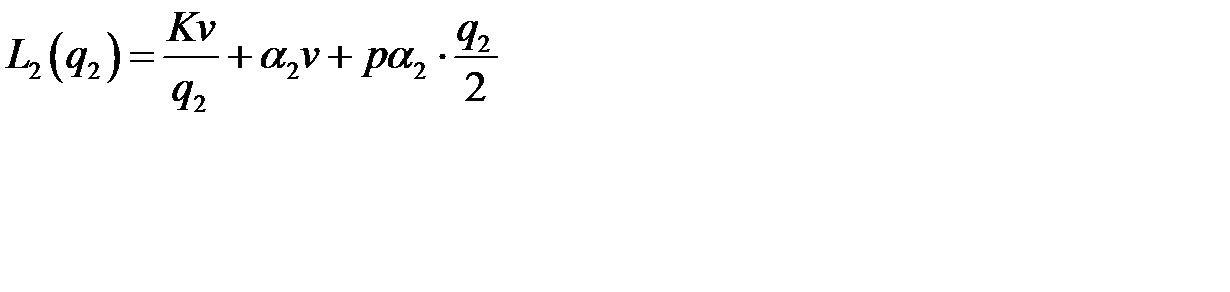 .
.
Вычислив производные
 ,
,  ,
,
приравняв их к нулю
 и
и 
найдем значения  и
и 
 и
и 
и минимальные издержки
 и
и  .
.
Имеются два значения  оптимальной партии поставки. Для выбора соответствующего значения
оптимальной партии поставки. Для выбора соответствующего значения  рассмотрим различные случаи значений
рассмотрим различные случаи значений  и Q, алгоритм их сравнения и выбора оптимальной партии.
и Q, алгоритм их сравнения и выбора оптимальной партии.
1. Вычисляем  . Если
. Если  , то учитывая, что
, то учитывая, что  , оптимальной партией будет
, оптимальной партией будет  .
.
2. Если  , то вычисляем
, то вычисляем  и разность
и разность  , где
, где 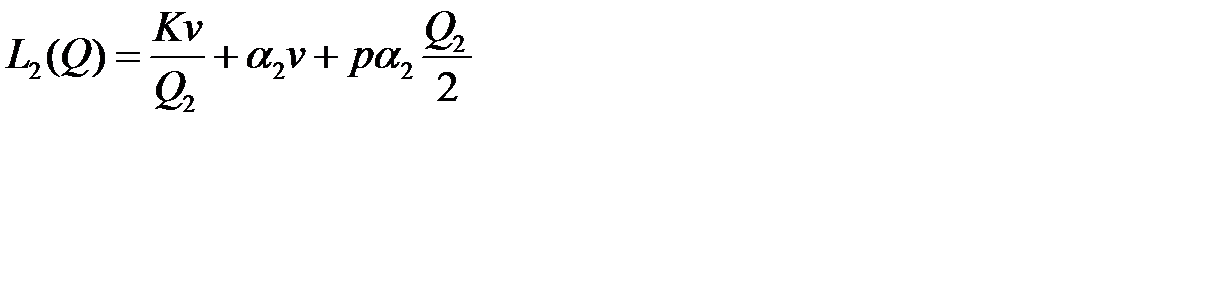 . Если
. Если  , то
, то  . Если
. Если  , то
, то  .
.
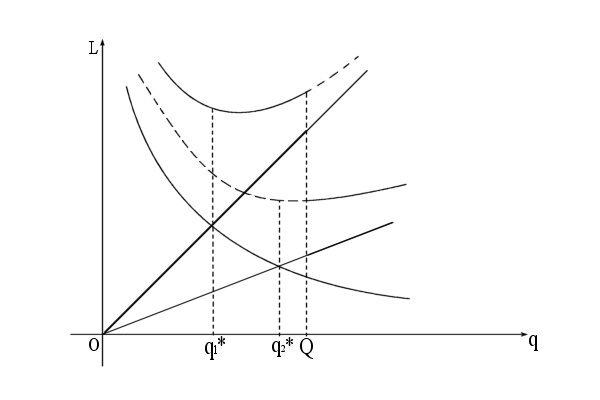
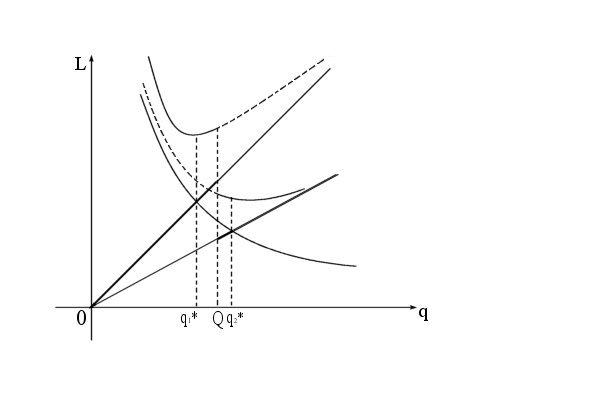
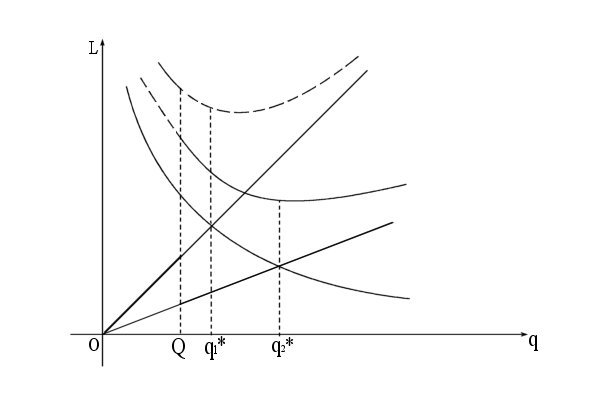
Эти выводы можно пояснить на рисунке 11.6 (а, б, в).
Пусть  и
и  (рис.11.6, а), то сравниваем
(рис.11.6, а), то сравниваем  и
и  . Если
. Если  и учитывая, что
и учитывая, что  , определяем оптимальную партию
, определяем оптимальную партию  . Пусть
. Пусть  и
и  . Тогда для определения оптимальной партии сравниваем
. Тогда для определения оптимальной партии сравниваем  с
с  : если
: если  , то
, то  , если
, если  , то
, то  , если
, если  и
и  , то
, то  .
.
 а) б)
а) б)
в)
Рисунок 11.6
Пример 11.4. Сборочное предприятие заказывает подшипники заводу. Спрос на них 5000 ед. в год. Подшипниковый завод выпускает различные подшипники партиями. Стоимость переналадки составляет 500 ден. ед. Если заказ не превышает 2000 подшипников, то стоимость одного подшипника – 40 ден. ед., если же заказ не меньше 2000, то стоимость - 32 ден.ед. Издержки содержания заказа составляют 2% от стоимости единицы продукции. Определить оптимальную партию заказа.
Решение. В задаче заданы следующие величины: спрос v = 5000 штук в год; К = 500 ден. ед.; Q =2000 штук;  ден. ед.;
ден. ед.;  ден. ед. за штуку; p=2%, тогда
ден. ед. за штуку; p=2%, тогда  . Применим сформулированный алгоритм. Вычислим
. Применим сформулированный алгоритм. Вычислим  :
:
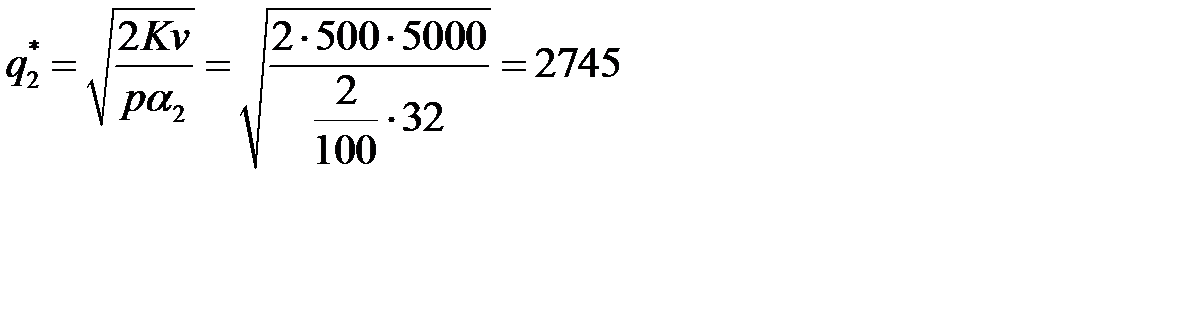 (подшипников).
(подшипников).
Так как  , то оптимальная партия
, то оптимальная партия  подшипников. Минимальные издержки в год составляют:
подшипников. Минимальные издержки в год составляют:
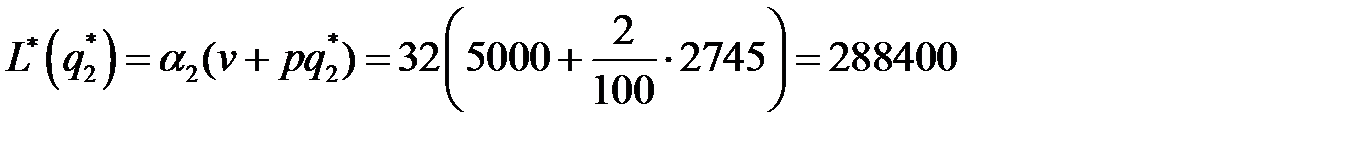 (ден.ед.).
(ден.ед.).
Рассмотрим n-уровневую систему скидок. Предположим, что внутри промежутков  цены остаются постоянными и только проходя через размеры заказов
цены остаются постоянными и только проходя через размеры заказов  ,
,  ,…
,…  снижаются, т.е.
снижаются, т.е.  . Обозначим экологически выгодные размеры заказов через
. Обозначим экологически выгодные размеры заказов через  . Алгоритм нахождения оптимального размера заказа состоит из числа шагов, не превышающего число n уровней цен.
. Алгоритм нахождения оптимального размера заказа состоит из числа шагов, не превышающего число n уровней цен.
1. Вычисляем  . Если
. Если  , то оптимальный размер заказа равен
, то оптимальный размер заказа равен  , т.е.
, т.е.  .
.
2. Если  , то определяем
, то определяем  . если
. если  , то сравниваем
, то сравниваем  с
с  и тогда, если
и тогда, если  , то
, то  , если же
, если же  ,то
,то  .
.
3. Если  , то вычисляем
, то вычисляем 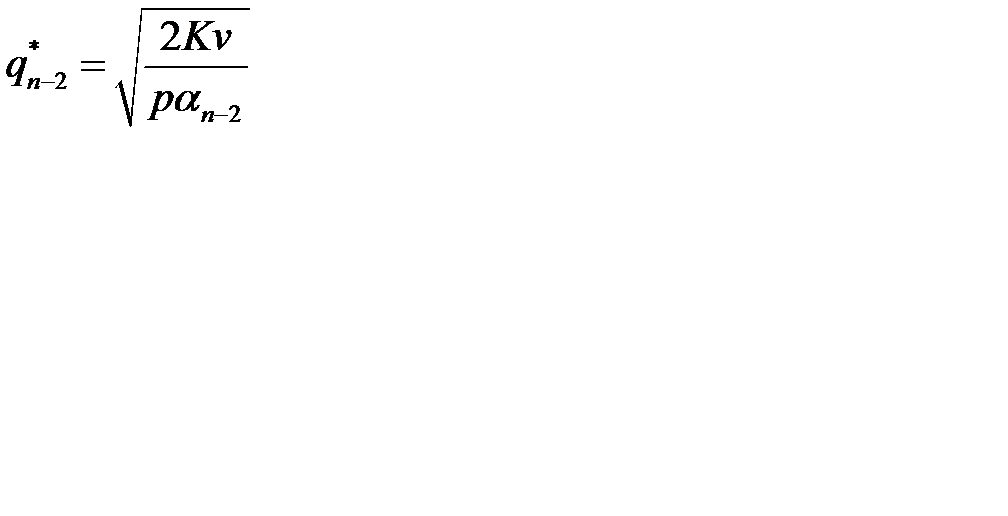 . Если
. Если  , то для определения оптимальной партии заказа сравниваем
, то для определения оптимальной партии заказа сравниваем 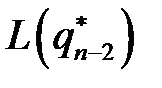 ,
,  и
и  и т.д. Этот процесс продолжаем до тех пор, пока
и т.д. Этот процесс продолжаем до тех пор, пока  . После этого сравниваем
. После этого сравниваем  ,
,  , …,
, …,  . Минимальному значению соответствует оптимальная партия заказа.
. Минимальному значению соответствует оптимальная партия заказа.
Пример 11.5. Цех выпускает стартеры различных видов. Издержки переналадки составляют 30 ден. ед. Потребность в стартерах различных видов постоянна и равна 600 штук в год. Себестоимость стартера зависит от величины заказа и приведена в таблице 11.1:
Таблица 11.1
| Величина заказа, штук | [1;150) | [150;400) | [400;+  ) )
|
| Цена за штуку, ден. ед. |
Издержки содержания составляют 2% от стоимости стартера. Установить оптимальную партию заказа.
Решение. В условии задачи приведены данные: стоимость переналадки оборудования - К=30 ден. ед.; спрос v = 600 штук в год; Q1 = 150 шт.; Q2 = 400 шт.;  ден. ед.;
ден. ед.;  ден. ед.;
ден. ед.;  ден. ед. за штуку; стоимость содержания p = 2% от стоимости единицы стартера. Применим алгоритм нахождения оптимального размера заказа.
ден. ед. за штуку; стоимость содержания p = 2% от стоимости единицы стартера. Применим алгоритм нахождения оптимального размера заказа.
Вычисляем 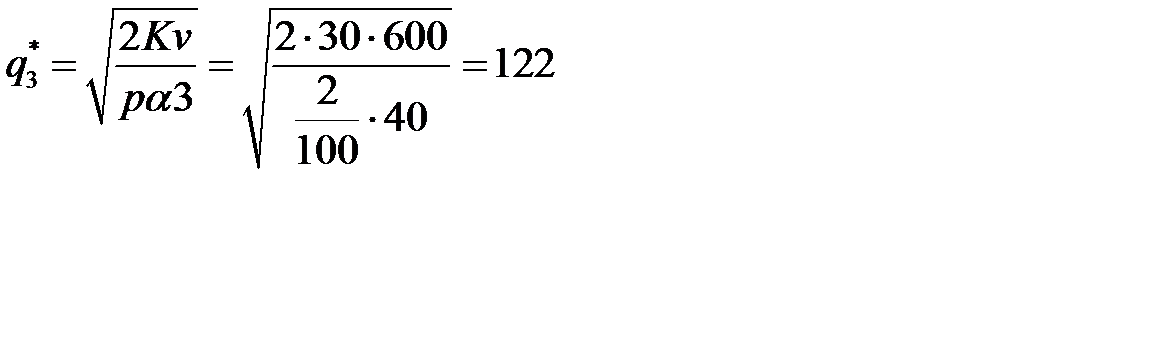 (штук).
(штук).
Так как  = 400, то вычисляем
= 400, то вычисляем 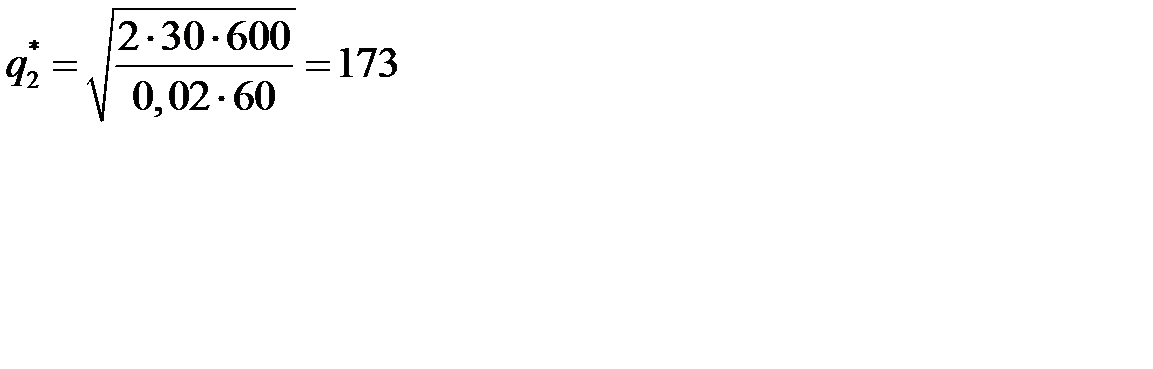 (штуки).
(штуки).
Поскольку  и
и  , то вычисляем разность
, то вычисляем разность 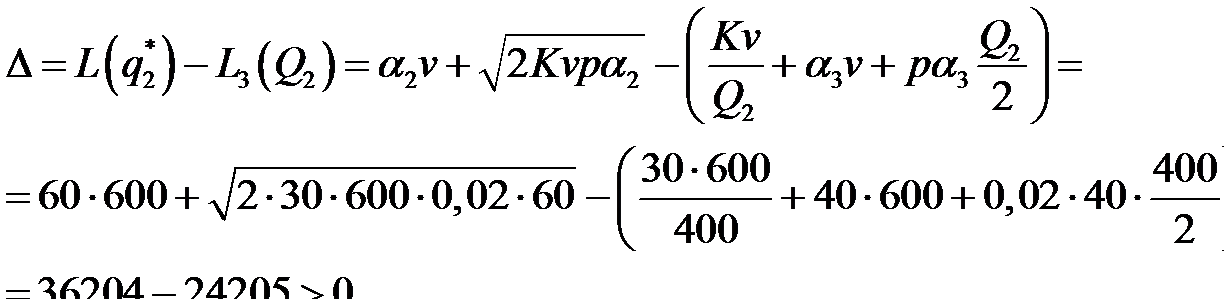
Значит  и минимальному значению соответствует минимальная партия заказа
и минимальному значению соответствует минимальная партия заказа  стартеров.
стартеров.
Лекция 12 Экономико-математические методы и модели управления социально-культурной сферой (продолжение)
Вопросы, изучаемые на лекции:
12.1. Многопродуктовые модели управления производством, поставками и запасами
12.1.1.Раздельная оптимизация
12.1.2. Полное совмещение заказов
12.2. Модели управления запасами со случайным спросом
12.2.1. Однопериодная модель со случайным спросом
12.2.2. Модель при наличии страхового запаса
Дата добавления: 2015-09-29; просмотров: 1025;
