Модели с конечной интенсивностью поступления заказа

В предыдущих моделях предполагалось, что партия заказа поступает мгновенно. Однако в ряде случаев выгоднее доставлять партию по частям с интенсивностью . Система может работать без дефицита, если интенсивность поставок значительно превосходит интенсивность потребления . Величина будет показывать скорость увеличения количества продукции на складе.

Динамика уровня запаса (рисунок 11.1) характеризуется следующими предположениями:

- в начальный момент времени запас равен нулю;

-в течение времени запас одновременно и поступает и расходуется (это время накопления запаса);

- в течение времени запас только расходуется (это время расходования запаса).

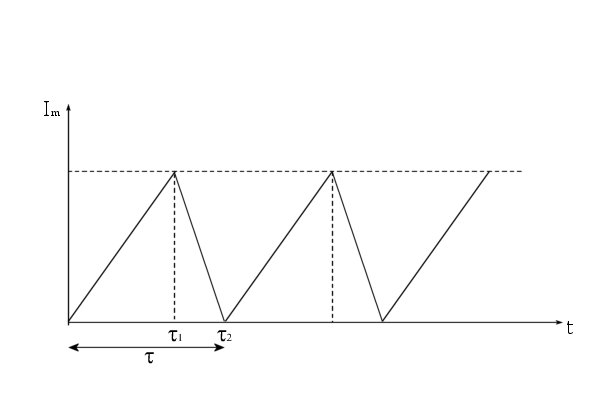
Рисунок 11.1

Длина цикла . Максимальный наличный запас будет равен:

, .

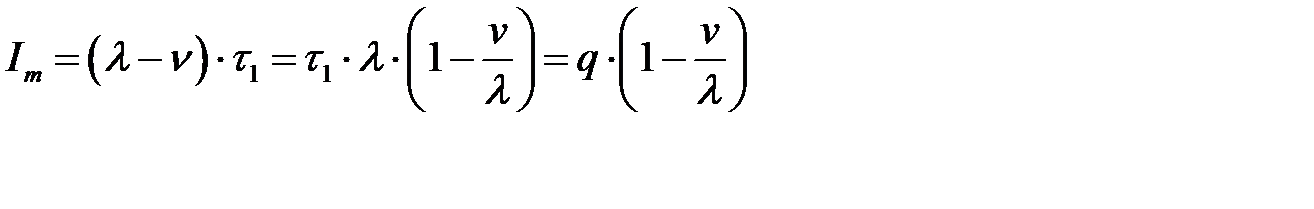Издержки системы в единицу времени являются функцией и равны сумме двух слагаемых:

.

Вычислив производную , приравняв ее к нулю

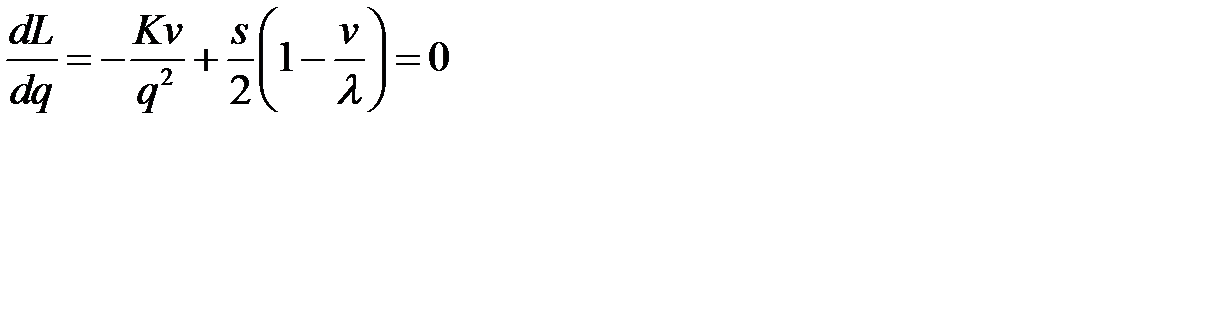, найдем величину оптимальной партии поставки:

.

Оптимальный период возобновления заказа:

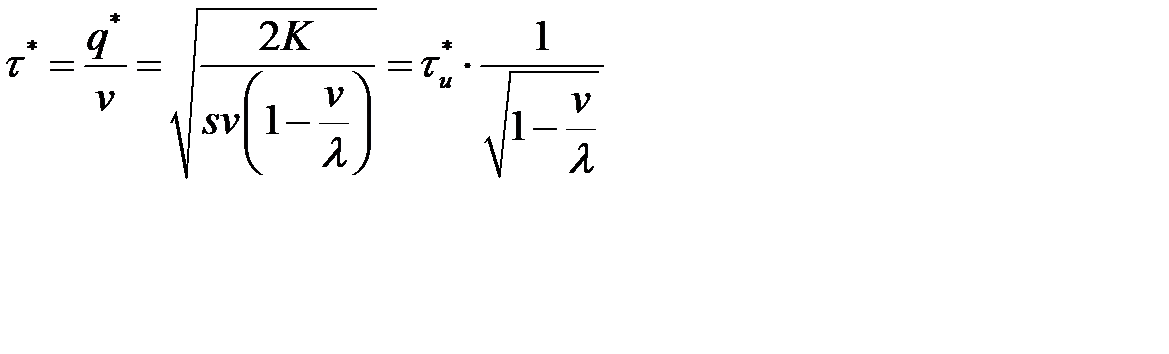и его составляющие:

- время накопления запаса

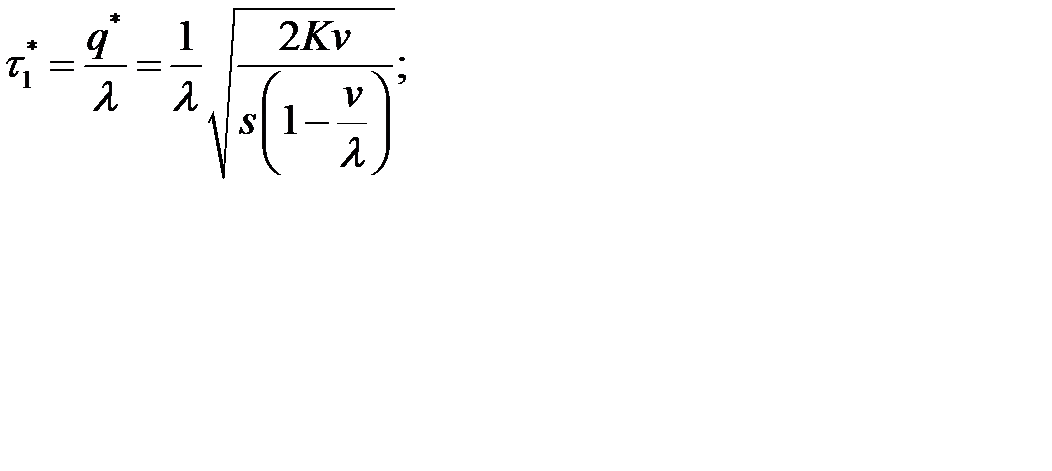
- время расходования запаса

.

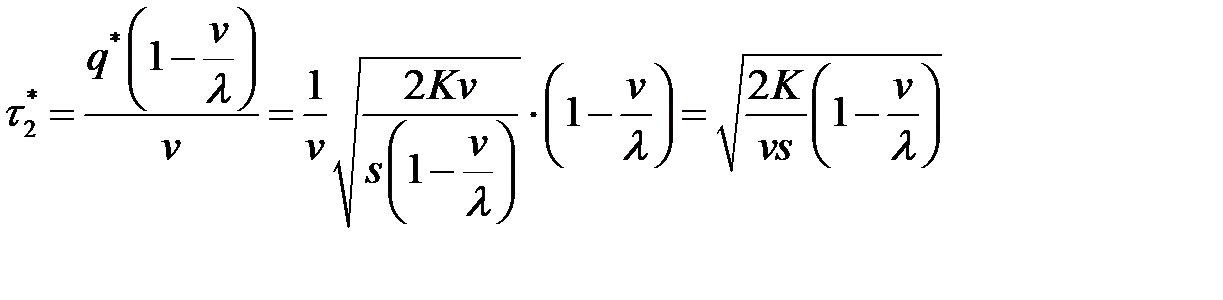Минимальные издержки в единицу времени равны

,

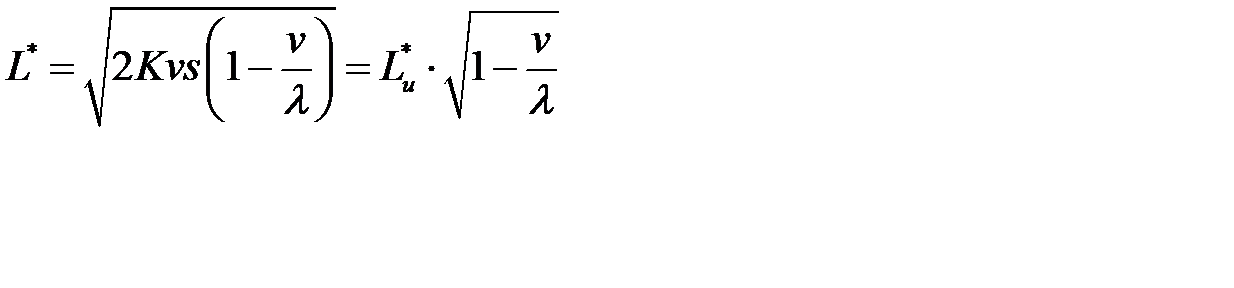( , , - оптимальные параметры модели Уилсона).

В случае, , когда интенсивность поставки значительно больше интенсивности потребления, то и оптимальные параметры этой модели будут равны оптимальным параметрам модели Уилсона.

Предположим, что на выполнение заказа требуется время . Тогда если , то точка заказа вычисляется по формуле: .

Если же , то точка заказа равна: .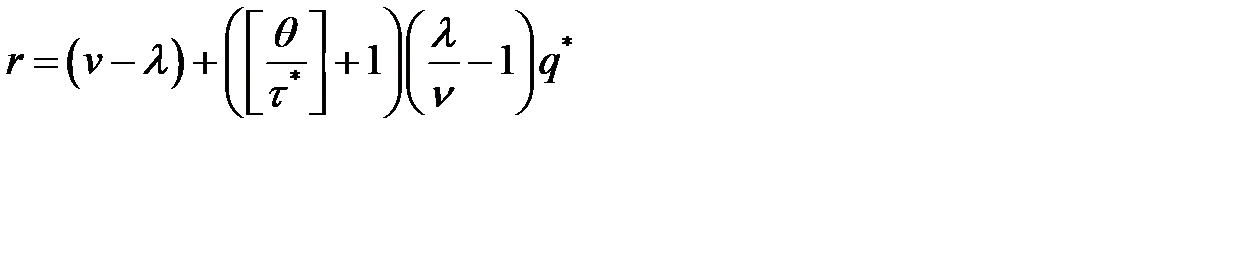

Моменты повторения заказа вычисляются по формуле

Модель оптимальной партии с конечной интенсивностью поступления может быть использована при определении оптимальной партии запуска продукции в производство. При этом К определяют издержки переналадки оборудования.

Пример 11.1. Фирма по производству соков выпускает партиями 10 различных сортов (соков) на одном и том же оборудовании. Спрос на каждый вид соков известен и составляет 5000 л. в год. Фиксированные издержки переналадки (связаны с очисткой и некоторой перенастройкой оборудования перед выработкой данного вида соков) равны 500 ден. ед. Стоимость содержания 1000 л. равная 20 ден. ед. в год. Производительность фирмы – 50000 л. в год. Время реализации заказа (от его получения до выдачи готовой продукции) – 1,5 месяца. Определить оптимальный размер партии производства одного вида соков, минимальный период возобновления производства партии одного вида сока, точку заказа и среднегодовые издержки исходя из того, что дефицит запаса на складе фирмы не допускается. Построить графическую модель изменения динамики производства соков.

Решение. В задаче определены начальные данные:

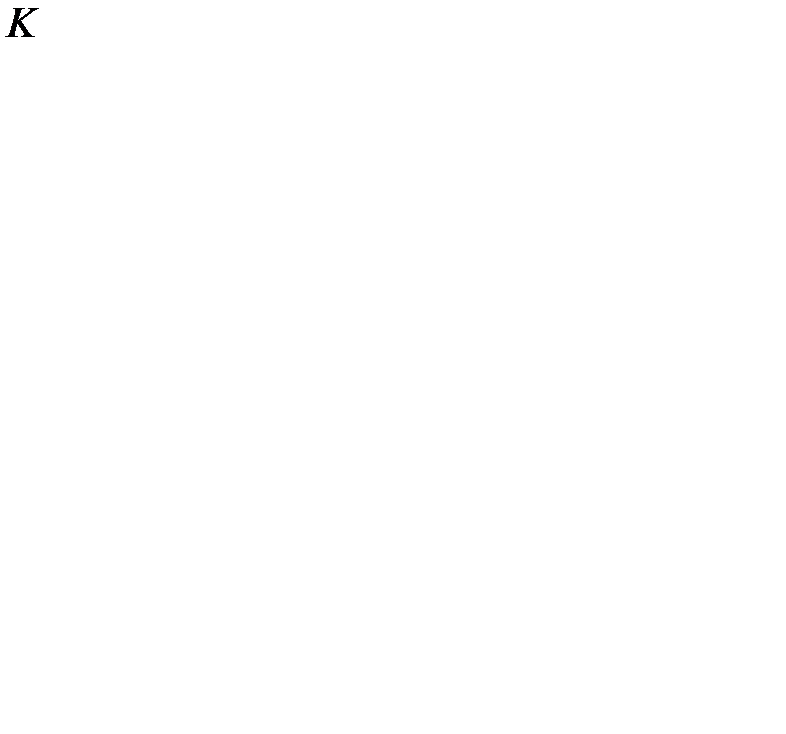= 500 ден. ед.; n = 5000 л. в год; l = 50000 л. в год; s = 20 ден. ед. за 1000 л. в год; q=1,5 мес. =0,125 года.

Применим модель с конечной интенсивностью поступления заказа и найдем оптимальные параметры работы фирмы:

- минимальная партия производства одного вида сока:

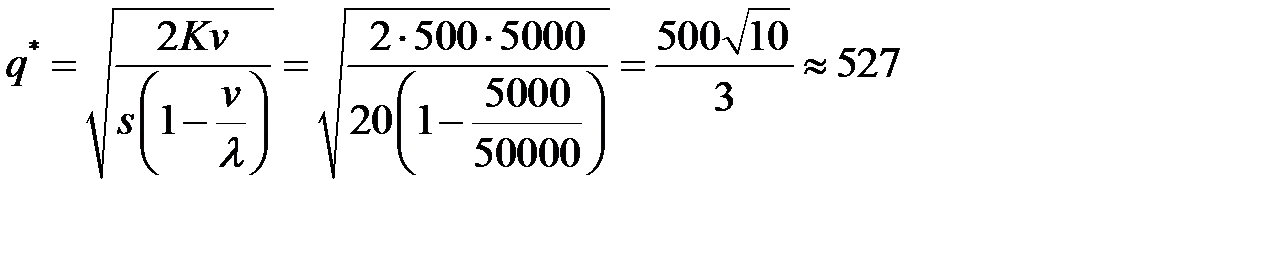(литров);

- время производства партии одного вида сока:

года (дня);

- время реализации партии одного вида сока:

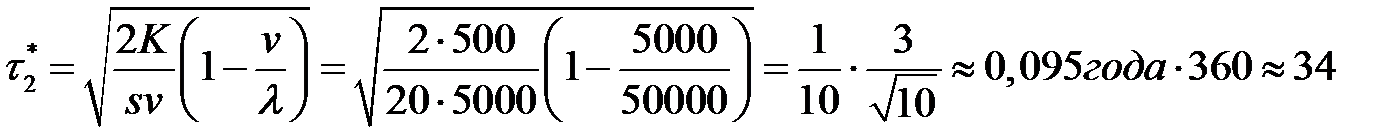дня;

- минимальный период возобновления производства партии одного вида сока:

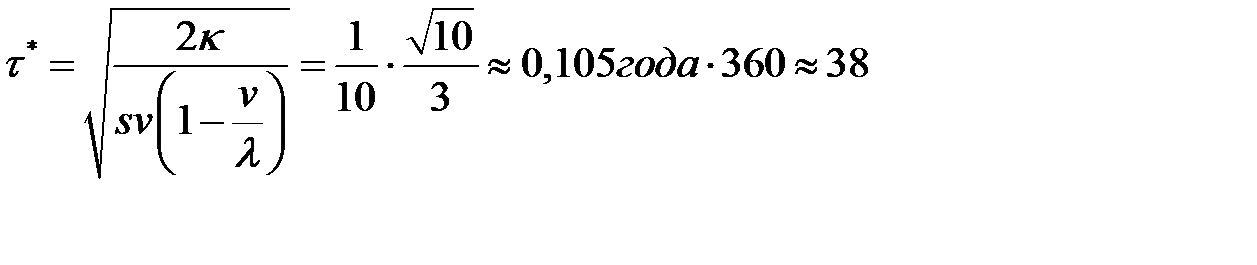дней;

-минимальные издержки работы фирмы по производству соков за год составят:

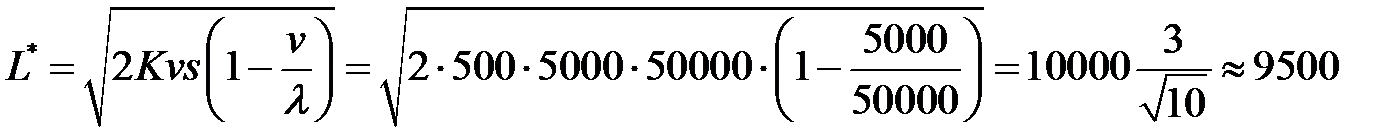(ден. ед.).

Поскольку 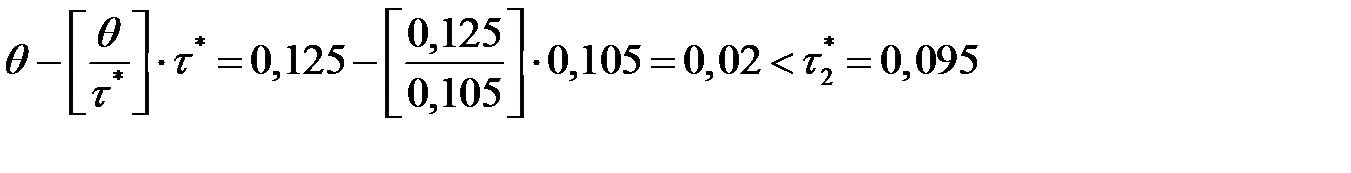, то точку заказа вычислим по формуле:

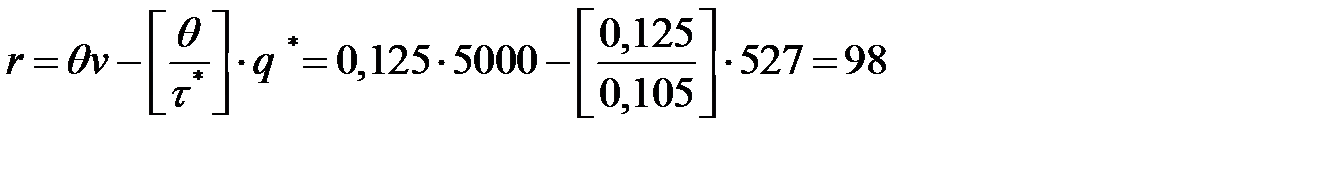(литров).

Если предположить, что фирма работает в стационарном режиме и начала поставлять очередную партию с 1 января, то следующая партия должна быть размещена в момент 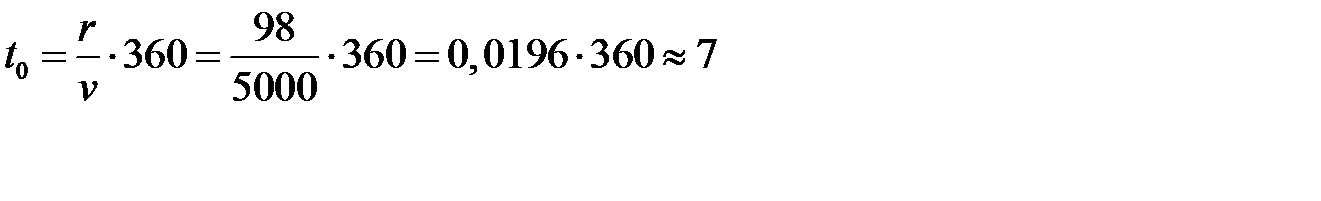(января). Следующие заказы должны быть размещены в моменты :

(января); (января) и т.д.

Для построения графика изменения динамики найдем максимальный уровень наличного запаса:

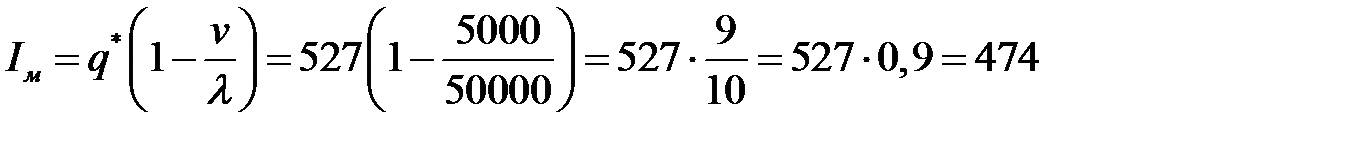(литра).

4 38 76

Рисунок 11.2