Модель с дефицитом, когда неудовлетворенные требования ставятся на учет
В случае, когда потери из-за дефицита сравнимы с издержками хранения, дефициты допускаются. При этом требования, поступающие в моменты дефицита, берутся на учет. При прибытии очередной партии поставки сначала удовлетворяется задолженный спрос, а затем остальные требования по мере поступления. Динамика изменения уровня запаса, в предположении что  - партия поставки, характеризуется следующим образом.
- партия поставки, характеризуется следующим образом.
В начальный момент времени уровень запаса равен максимальной величине наличного запаса  , где
, где  - величина задолженного спроса. Наличный запас расходуется за время
- величина задолженного спроса. Наличный запас расходуется за время  , которое называется временем существования наличного запаса. Затем поступающие требования берутся на учет в течение времени
, которое называется временем существования наличного запаса. Затем поступающие требования берутся на учет в течение времени  , называемым временем дефицита. При поступлении очередной партии в первую очередь удовлетворяется задолженный спрос, а затем пополняется запас (см. рисунок 11.3).
, называемым временем дефицита. При поступлении очередной партии в первую очередь удовлетворяется задолженный спрос, а затем пополняется запас (см. рисунок 11.3).
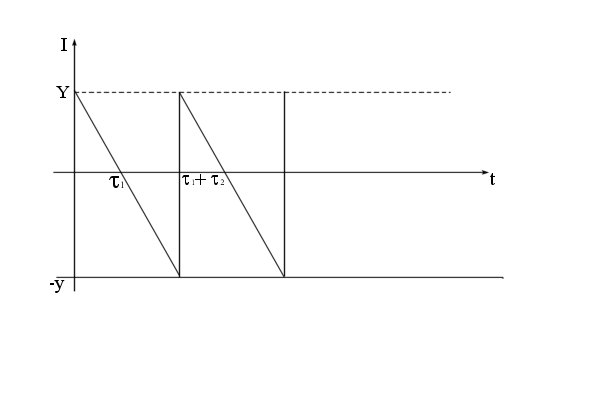
Рисунок 11.3
Убытки, связанные с дефицитом единицы запаса в единицу времени, обозначим  . Тогда издержки цикла состоят:
. Тогда издержки цикла состоят:
· из издержек 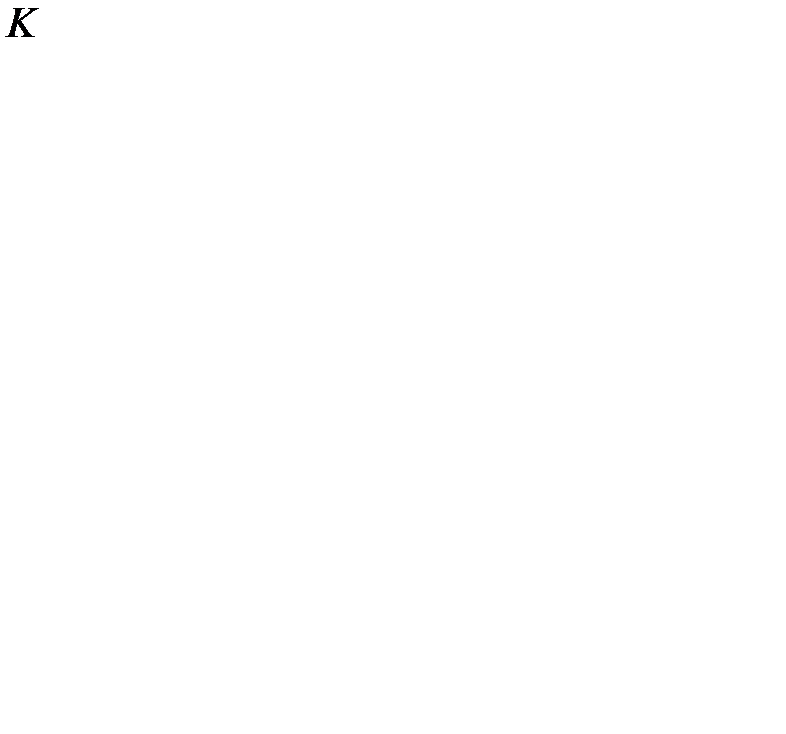 размещения заказа, не зависящих от величины партии
размещения заказа, не зависящих от величины партии  ;
;
· из издержек на хранение продукции, пропорциональных средней величине запаса 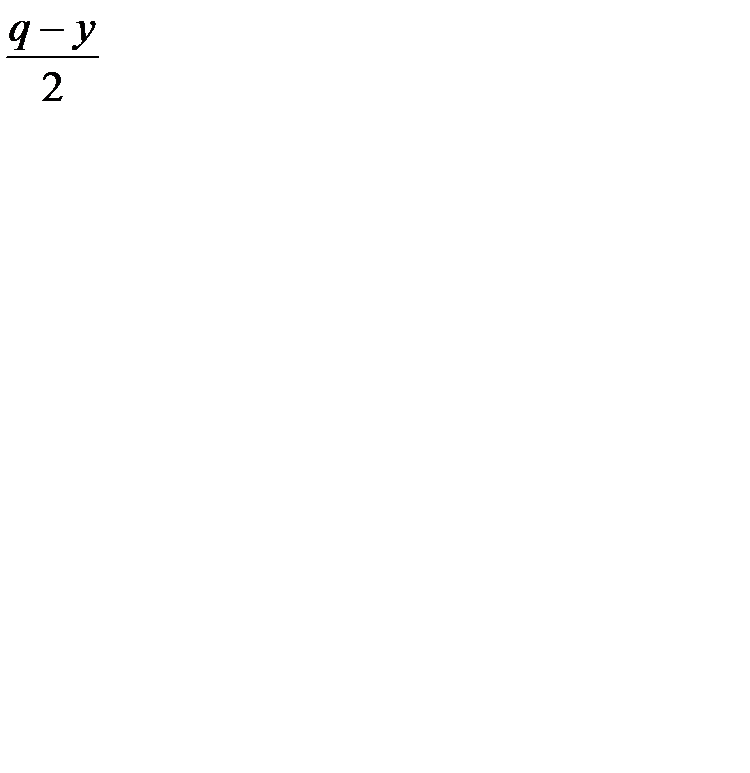 и времени его существования
и времени его существования 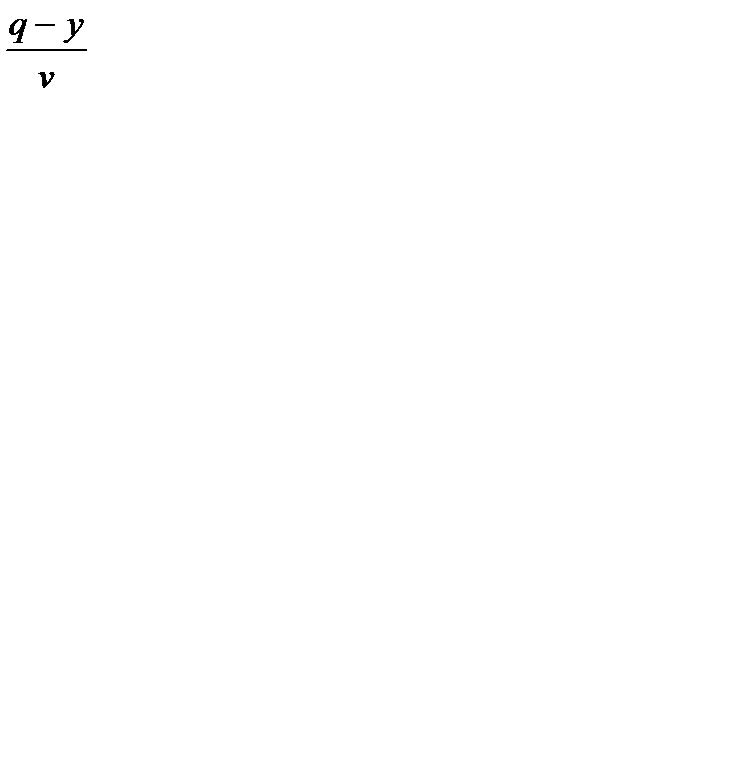 ;
;
· из издержек от дефицита, пропорциональных средней величине дефицита  и времени его существования
и времени его существования  , т.е.
, т.е.
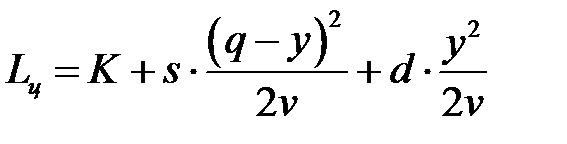 .
.
Разделим издержки цикла на его величину 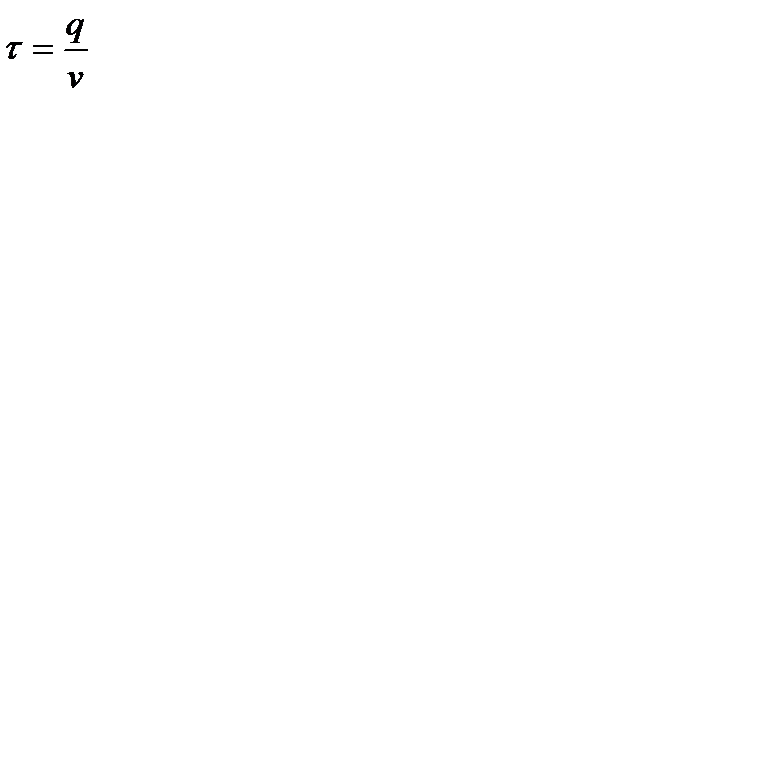 и получим издержки работы системы в единицу времени:
и получим издержки работы системы в единицу времени:
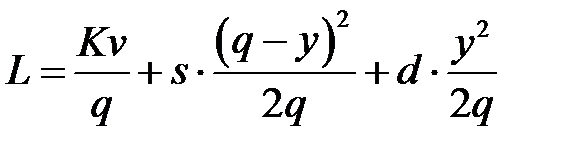 . (11.1)
. (11.1)
Издержки работы системы в единицу времени являются функцией двух переменных  и
и  , т.е.
, т.е.  . Применив необходимые условия экстремума функции 2-ух переменных, т. е. вычислив частные производные
. Применив необходимые условия экстремума функции 2-ух переменных, т. е. вычислив частные производные

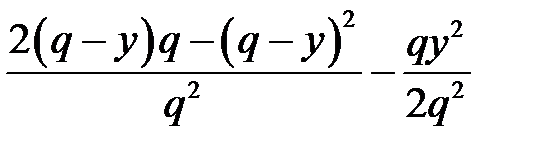
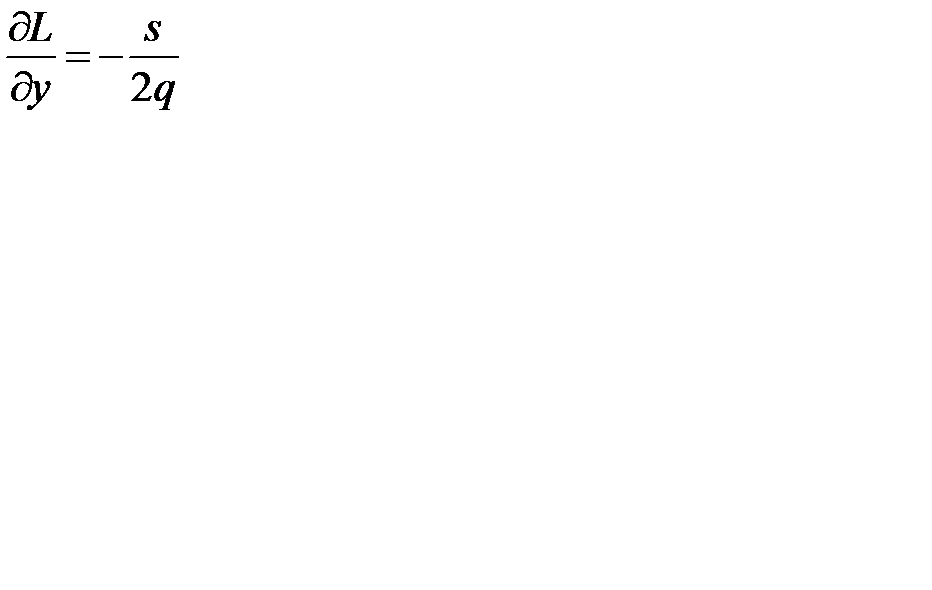
 .
.
и приравняв их нулю, получим систему:
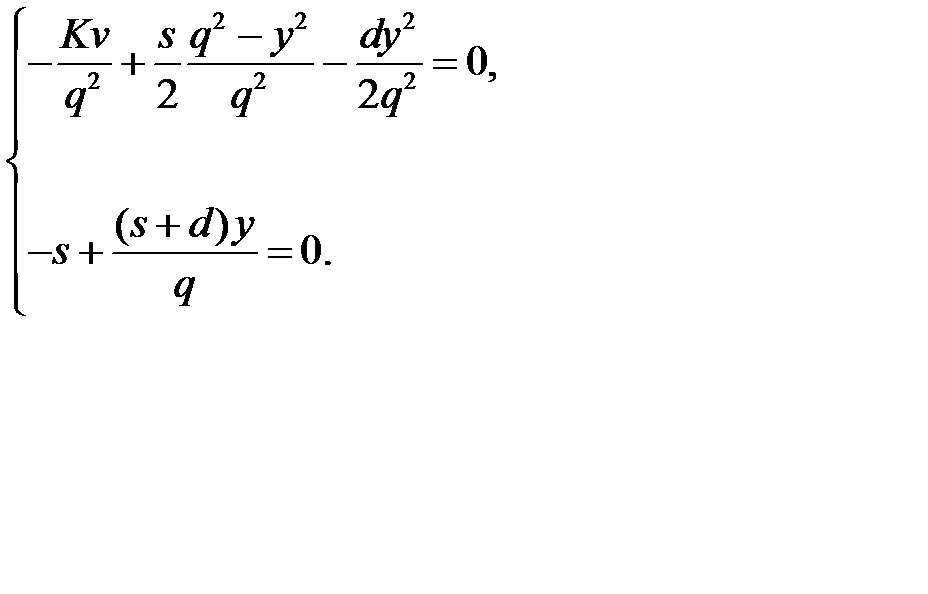
Решив систему, находим оптимальные значения  и
и  :
:
 ;
; 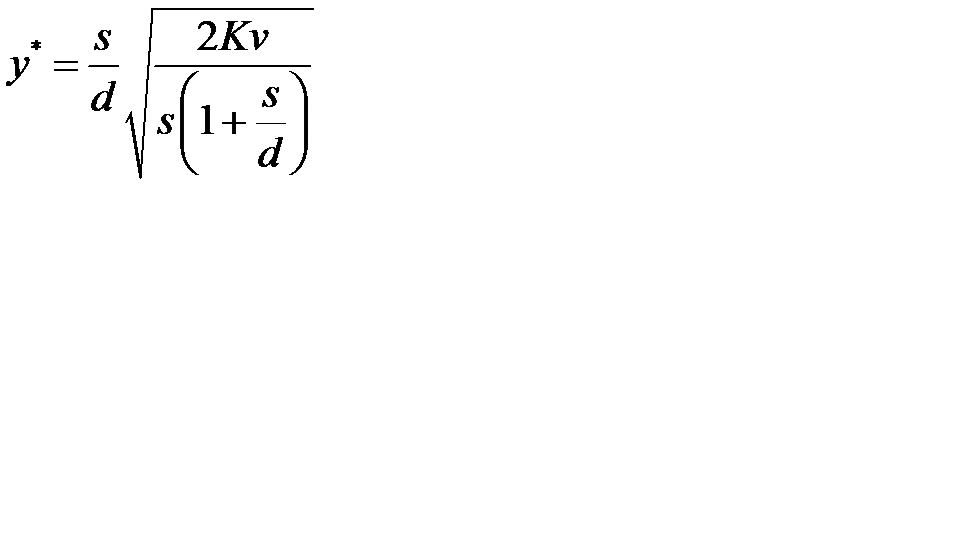
Вычислив частные производные второго порядка 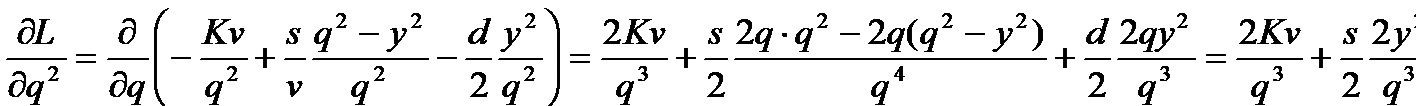
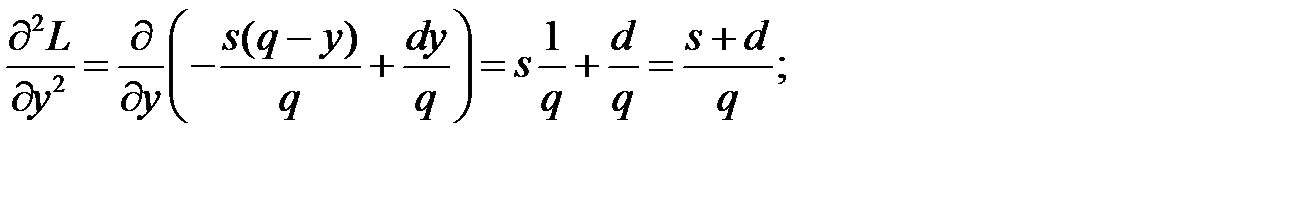
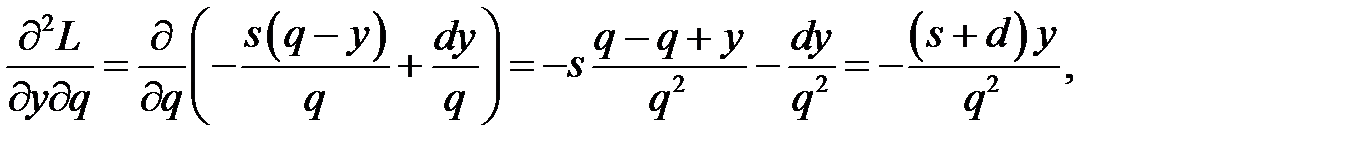
и их значения при 
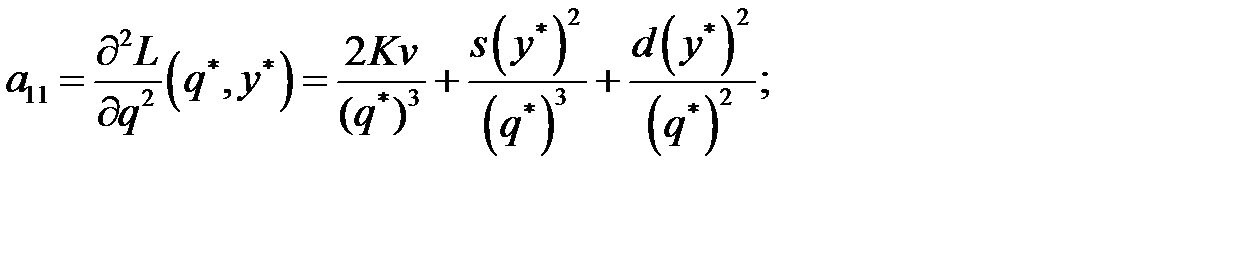
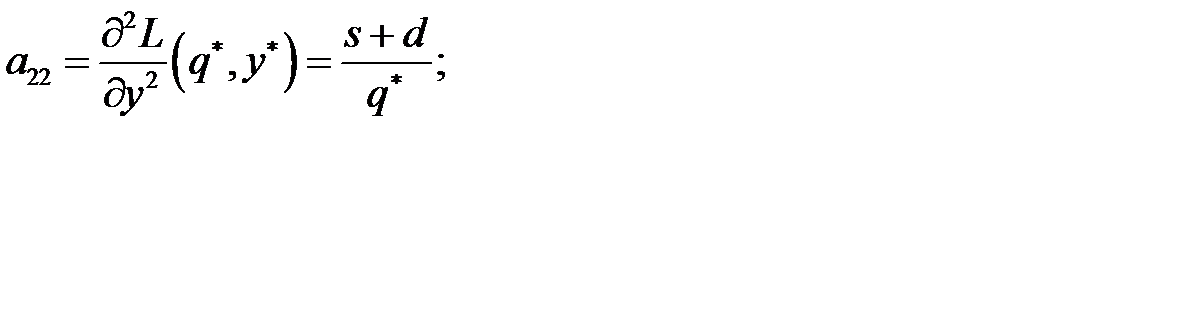
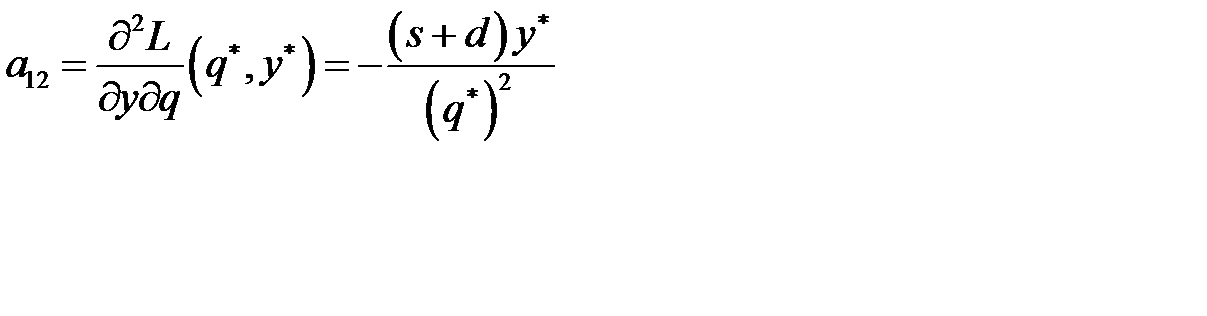
составим выражение
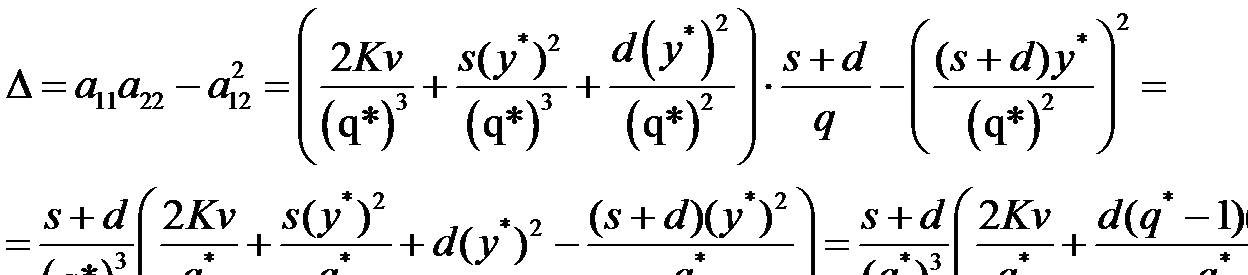
Так как  > 0 и
> 0 и  , то при
, то при  и
и  издержки достигают минимального значения.
издержки достигают минимального значения.
Подставив найденные значения  и
и  в формулу (11.1), найдем минимальные издержки работы системы:
в формулу (11.1), найдем минимальные издержки работы системы:
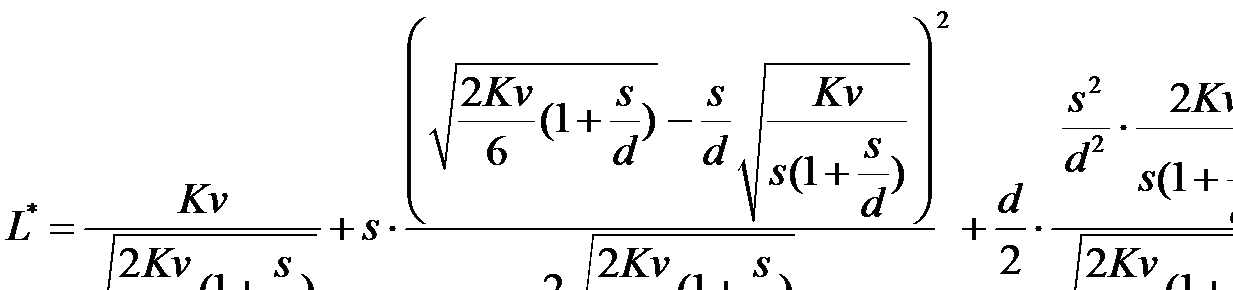
Зная оптимальные значения  и
и  , найдем:
, найдем:
-максимальный уровень наличного запаса
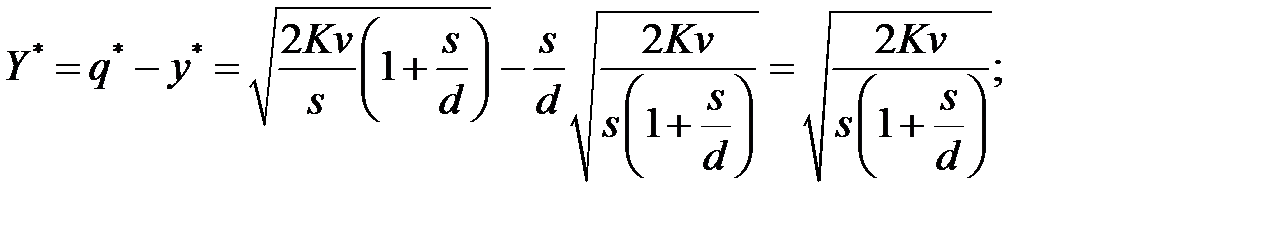
- время существования наличного запаса
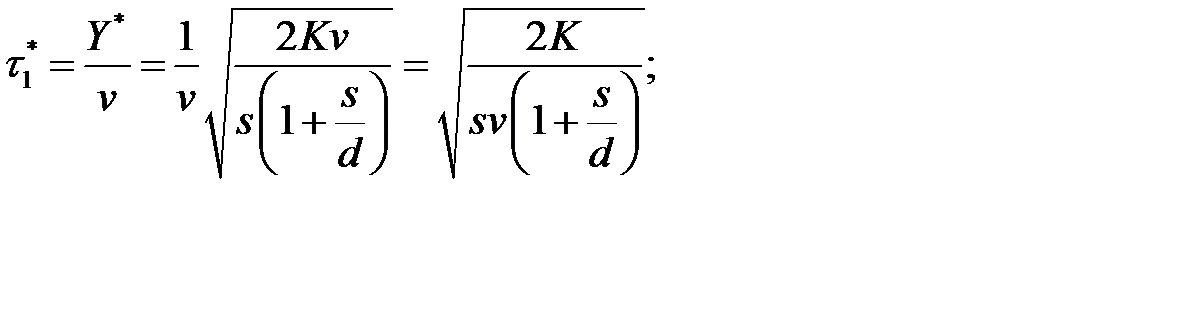
- время существования дефицита
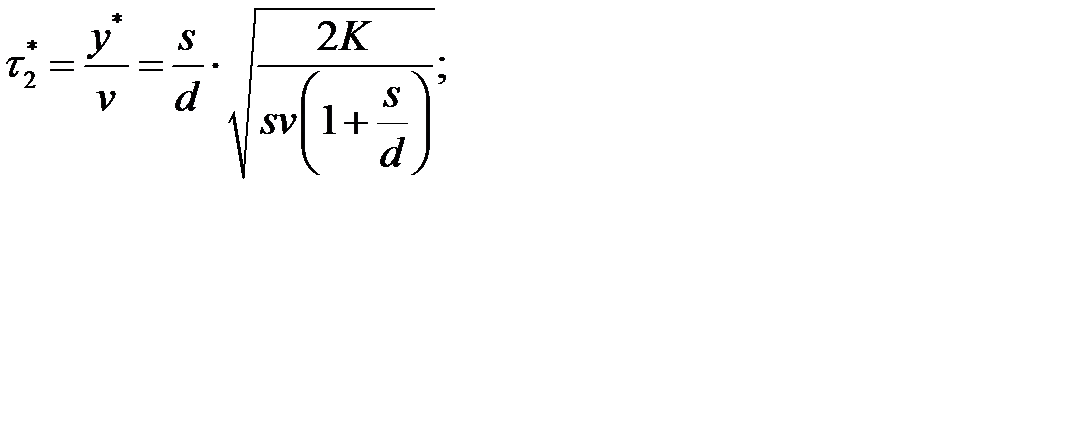
- длину цикла

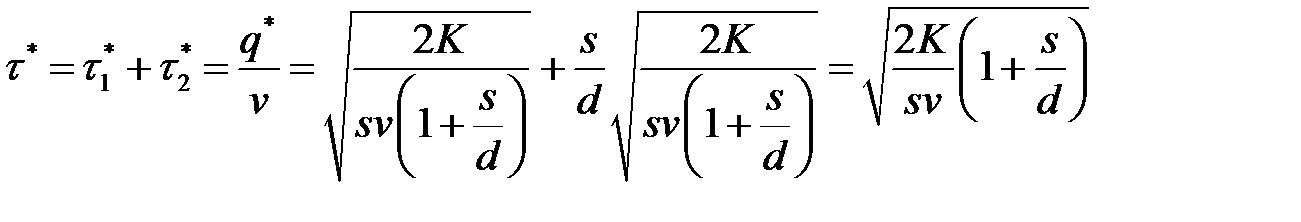 .
.
Отметим, что в рассматриваемой модели
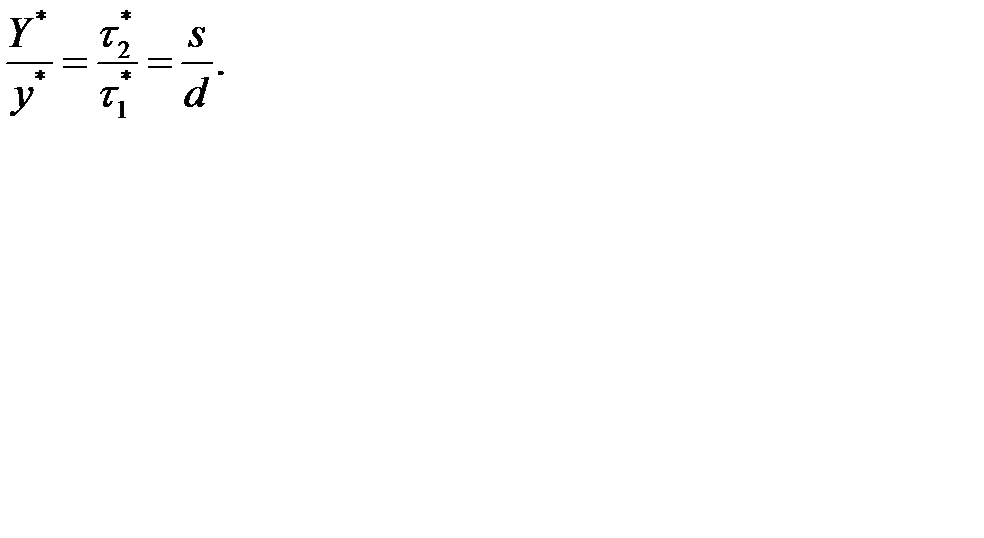
Кроме того, при высоких штрафах за дефицит, когда  , рассматриваемая модель превращается в модель Уилсона. Когда неудовлетворенные требования ставятся на учет, точка заказа может быть рассчитана по формуле:
, рассматриваемая модель превращается в модель Уилсона. Когда неудовлетворенные требования ставятся на учет, точка заказа может быть рассчитана по формуле:

Поскольку  может быть отрицательной величиной, то заказ должен размещаться в момент, когда величина требований, поставленных на учет, равна
может быть отрицательной величиной, то заказ должен размещаться в момент, когда величина требований, поставленных на учет, равна  .
.
Пример 11.2. Спрос на продукцию составляет 1900 тонн в год. Стоимость хранения, включая потери от иммобилизации средств в запасах и связанные со снижением цен, в случае нереализации продукции, равна 19 ден. ед. за 1 тонну в год. Издержки размещения заказа составляют 200 ден. ед. Неудовлетворенные требования берутся на учет. Удельные издержки дефицита составляют 81 ден. ед. за нехватку 1 тонны в течение года. Среднее время реализации заказа – 1 месяц. Определить оптимальную партию поставки, максимальную величину размещения заказа и минимальные издержки функционирования системы. Построить графическую модель изменения динамики спроса на продукцию.
Решение. В задаче определены начальные данные:  = 200 ден. ед.;
= 200 ден. ед.;
 = 1900 тонн в год; s = 19 ден. ед. за 1 тонну в год;
= 1900 тонн в год; s = 19 ден. ед. за 1 тонну в год;  = 81 ден. ед. за нехватку 1 тонны в год;
= 81 ден. ед. за нехватку 1 тонны в год; 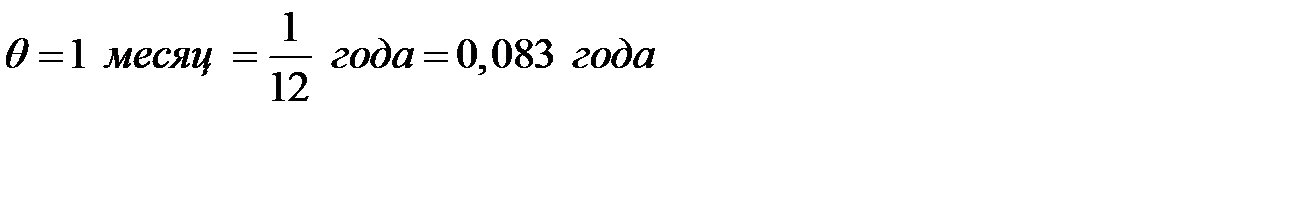 .
.
Применим модель с дефицитом и найдем оптимальные параметры работы системы:
- минимальную партию поставки продукции:
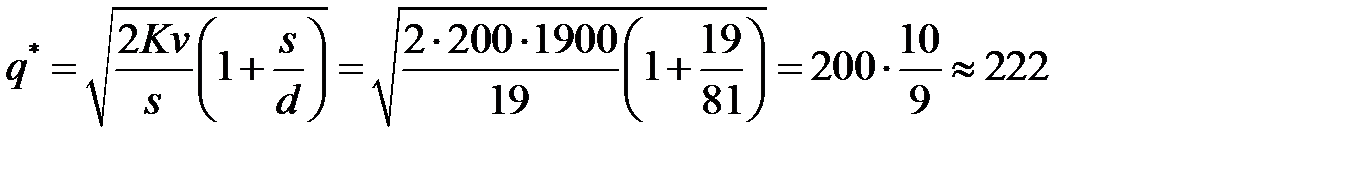 (тонны);
(тонны);
-максимальную величину задолженного спроса
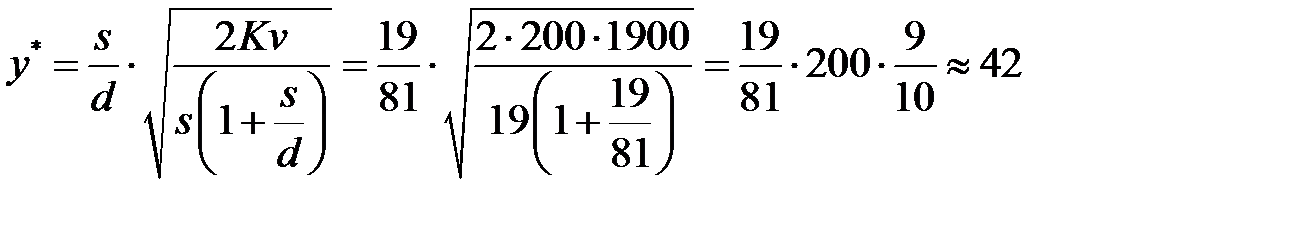 (тонны);
(тонны);
- максимальную величину наличного запаса
 (тонн);
(тонн);
-оптимальную величину цикла (минимальную величину возобновления заказа, интервал возобновления заказа)
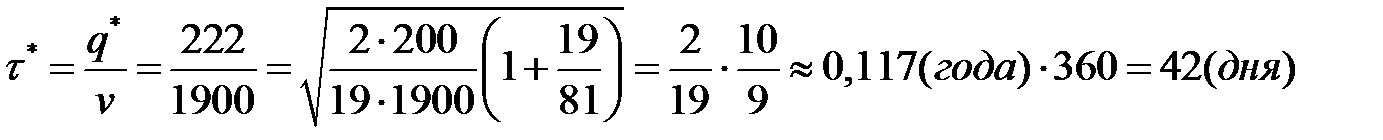 ;
;
- время существования наличного запаса
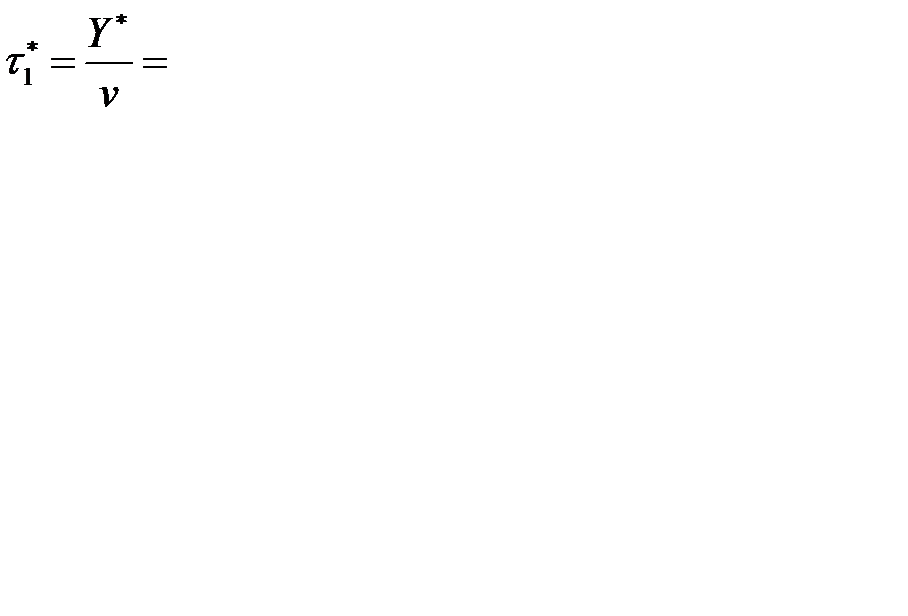
 (года) = 0,095
(года) = 0,095  (дня);
(дня);
- время существования дефицита
 (года) =
(года) =  (дней);
(дней);
- точку заказа
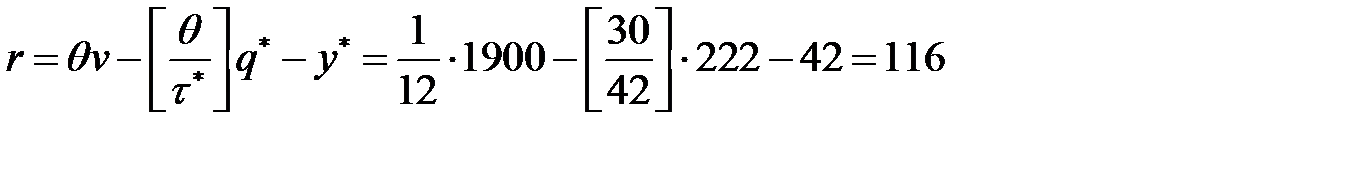 (тонн);
(тонн);
-минимальные издержки работы системы

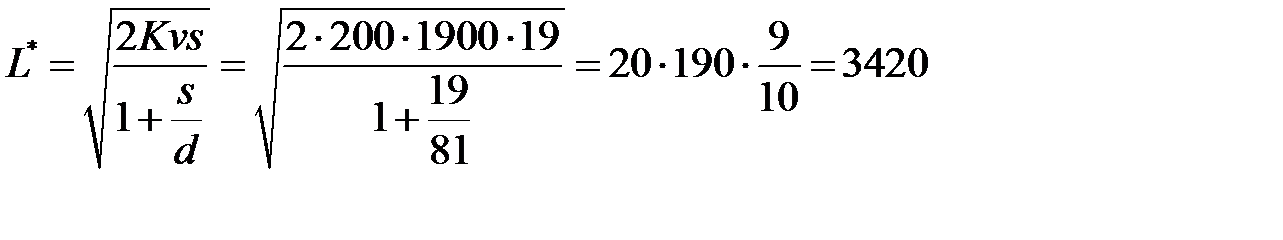 (ден. ед. в год).
(ден. ед. в год).
Динамика изменения уровня запаса изображена на рисунке 11.4.
 -42
-42
|
| 34 42 76 t |

Рисунок 11.4
Дата добавления: 2015-09-29; просмотров: 1146;
