Учет точки заказа
При построении модели Уилсона предполагалось, что заказы выполняются мгновенно. В действительности необходимо учитывать время их доставки. Пусть  время от момента размещения заказа до момента его появления у потребителя. Чтобы избежать дефицита, заказ должен подаваться в тот момент, когда в запасе еще имеется наличный ресурс, количество которого должно быть достаточно для удовлетворения потребности на время выполнения заказа. Величину наличного запаса, при котором подается заказ на пополнение, будем называть точкой возобновления заказа и обозначать
время от момента размещения заказа до момента его появления у потребителя. Чтобы избежать дефицита, заказ должен подаваться в тот момент, когда в запасе еще имеется наличный ресурс, количество которого должно быть достаточно для удовлетворения потребности на время выполнения заказа. Величину наличного запаса, при котором подается заказ на пополнение, будем называть точкой возобновления заказа и обозначать  . Пусть
. Пусть  - минимальный интервал между поставками (длина цикла), то при определении точки возобновления заказа рассматривается 3 случая:
- минимальный интервал между поставками (длина цикла), то при определении точки возобновления заказа рассматривается 3 случая:
а)  , б)
, б)  , в)
, в)  .
.
а) Если  , то в момент поступления очередной партии следует подавать заказ на следующую очередную партию. Точка заказа при
, то в момент поступления очередной партии следует подавать заказ на следующую очередную партию. Точка заказа при  равна нулю:
равна нулю:  . Сумма наличного запаса и заказного ресурса в любой момент времени называется фиктивным уровнем
. Сумма наличного запаса и заказного ресурса в любой момент времени называется фиктивным уровнем  текущего запаса. При
текущего запаса. При  средний уровень фиктивного запаса равен:
средний уровень фиктивного запаса равен:

Динамика изменения текущего уровня фиктивности запаса при  показана на рисунке 10.2 пунктирной линией. От момента размещения заказа до момента прибытия заказа невыполненных заказов нет. Фиктивный уровень запаса совпадает с наличным.
показана на рисунке 10.2 пунктирной линией. От момента размещения заказа до момента прибытия заказа невыполненных заказов нет. Фиктивный уровень запаса совпадает с наличным.
| t* 2t* 3t* 4t* |
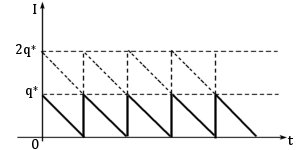
Рисунок 10.2
Средний уровень фиктивности запаса равен 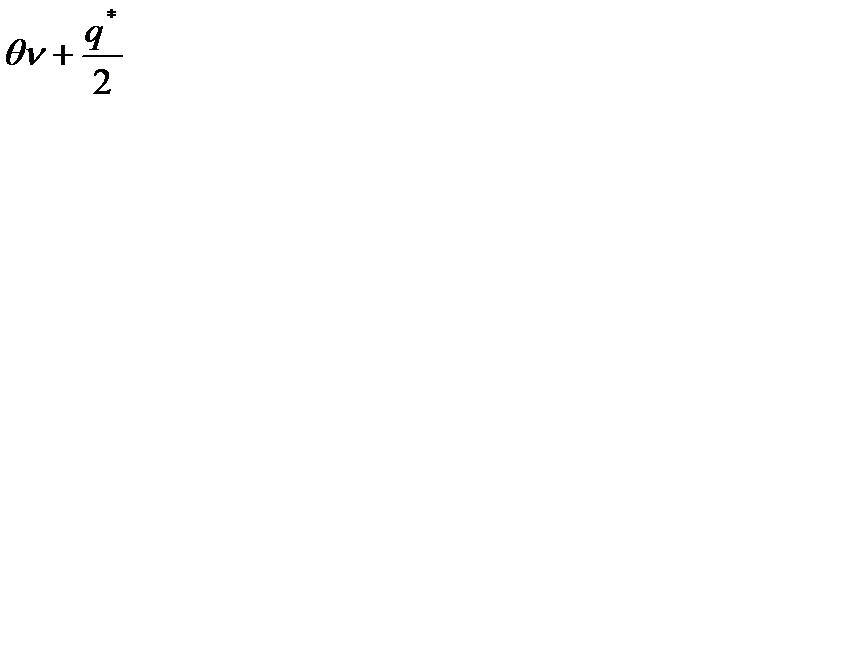 .
.
б) Если  (время выполнения заказа меньше длины одного цикла), то точка размещения заказа
(время выполнения заказа меньше длины одного цикла), то точка размещения заказа  . Средний уровень фиктивности запаса равен:
. Средний уровень фиктивности запаса равен:  . Динамика изменения фиктивного уровня запаса при
. Динамика изменения фиктивного уровня запаса при  показана на рисунке 10.3., где
показана на рисунке 10.3., где  . От момента размещения заказа до момента прибытия заказа невыполненных заказов нет.
. От момента размещения заказа до момента прибытия заказа невыполненных заказов нет.
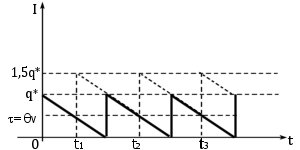
Рисунок 10.3
в) Если  , то точка размещения заказа вычисляется по формуле:
, то точка размещения заказа вычисляется по формуле:
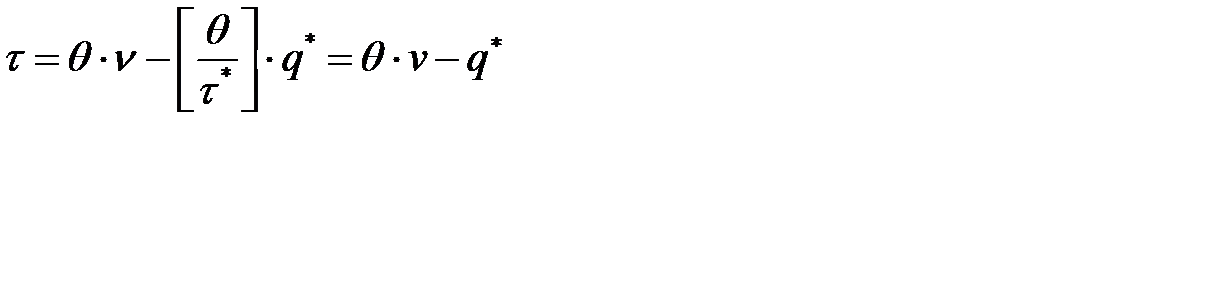 , где
, где  - целая часть числа
- целая часть числа  . Динамика изменения фиктивного уровня запаса при
. Динамика изменения фиктивного уровня запаса при  , приведена на рисунке 10.4, где
, приведена на рисунке 10.4, где  .
.
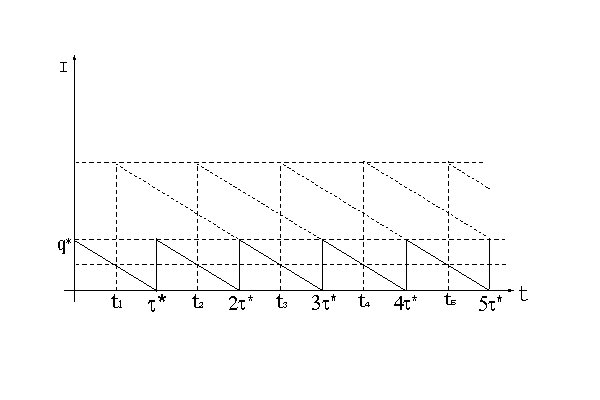
Рисунок 10.4
Для бездефицитной работы в системе в начальный момент времени необходим некоторый начальный запас  . Чтобы заказанная партия была доставлена не позже полного расходования начального запаса, заказ нужно разместить в момент времени
. Чтобы заказанная партия была доставлена не позже полного расходования начального запаса, заказ нужно разместить в момент времени  , где
, где  – фактический наличный начальный запас. Для бездефицитной работы величина фактического наличного начального запаса
– фактический наличный начальный запас. Для бездефицитной работы величина фактического наличного начального запаса  должна быть больше
должна быть больше  где
где  . Тогда
. Тогда  - время потребления фактического наличного начального запаса. Остальные заказы должны быть размещены в момент времени:
- время потребления фактического наличного начального запаса. Остальные заказы должны быть размещены в момент времени:

Пример 10.1. Предположим, что средняя потребность предприятия в сырье составляет 9 тыс. тонн в год. Издержки размещения заказа - 20 ден. ед., содержание одной тонны – 4 ден. ед. в год. Среднее время реализации заказа – 15 дней. Определить оптимальную партию поставки, периодичность возобновления заказа, точку размещения заказа, минимальный начальный наличный запас сырья, моменты повторения заказов, минимальные издержки на размещение заказов и их содержание. Построить график динамики изменения фиктивного уровня запаса.
Решение. В задаче заданы величины:  тонн в год;
тонн в год; 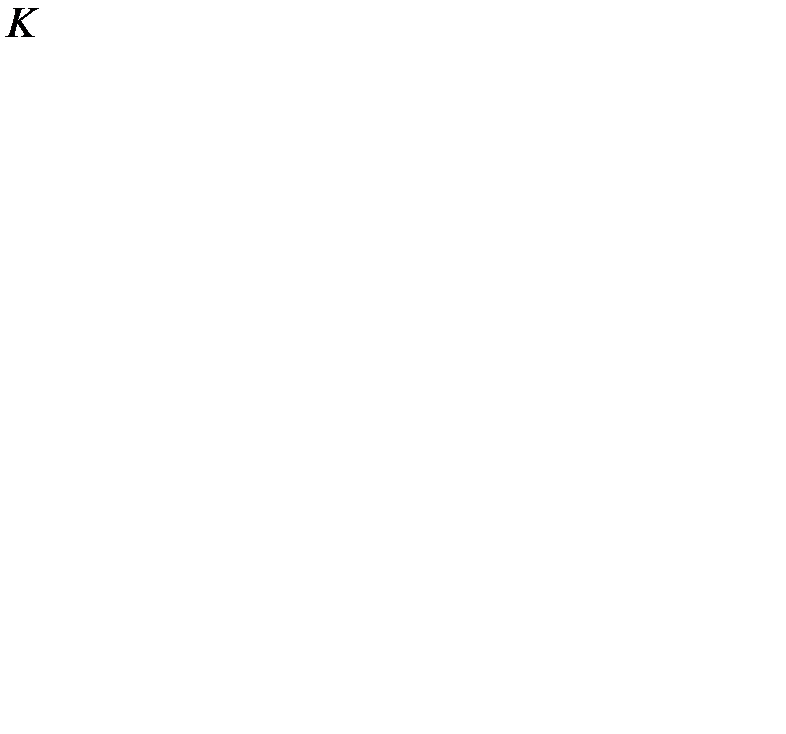 = 20 ден.ед.;
= 20 ден.ед.;  = 4 ден.ед.;
= 4 ден.ед.;  15 дней =
15 дней = 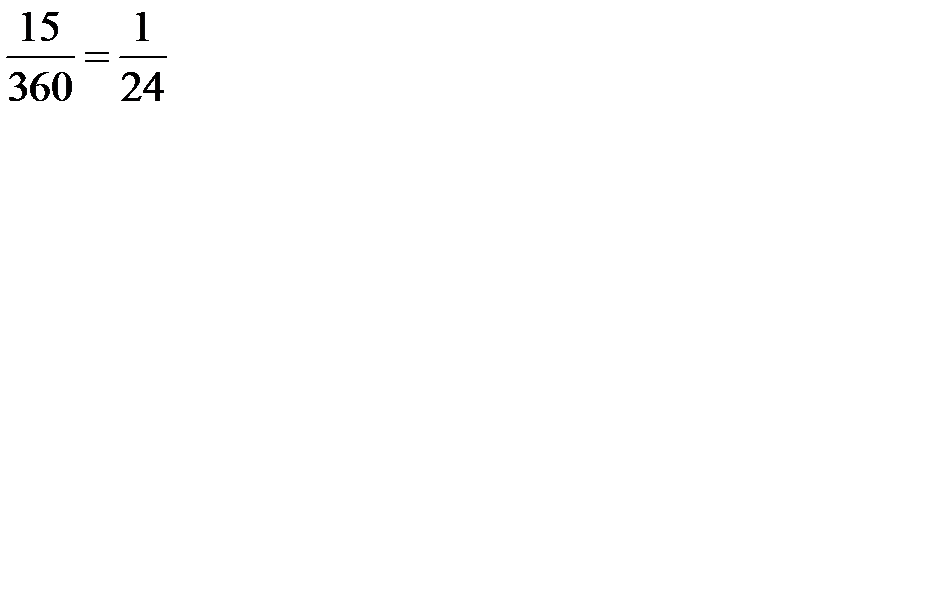 года = 0,042 года. Поскольку не определены условия доставки сырья, то считаем, что заказанная партия доставляется мгновенно. Следовательно, для определения оптимальных параметров работы предприятия применим модель Уилсона. Минимальную партию поставки сырья находим по формуле Уилсона:
года = 0,042 года. Поскольку не определены условия доставки сырья, то считаем, что заказанная партия доставляется мгновенно. Следовательно, для определения оптимальных параметров работы предприятия применим модель Уилсона. Минимальную партию поставки сырья находим по формуле Уилсона:
 (тонн).
(тонн).
Минимальный интервал возобновления поставки заказа:
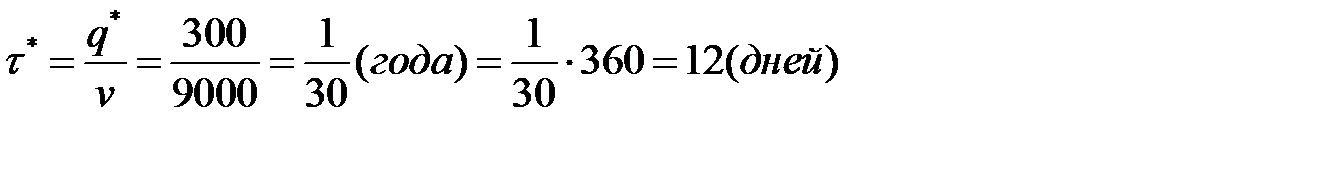 .
.
Так как время реализации заказа  , то точка размещения заказа, равна:
, то точка размещения заказа, равна: 
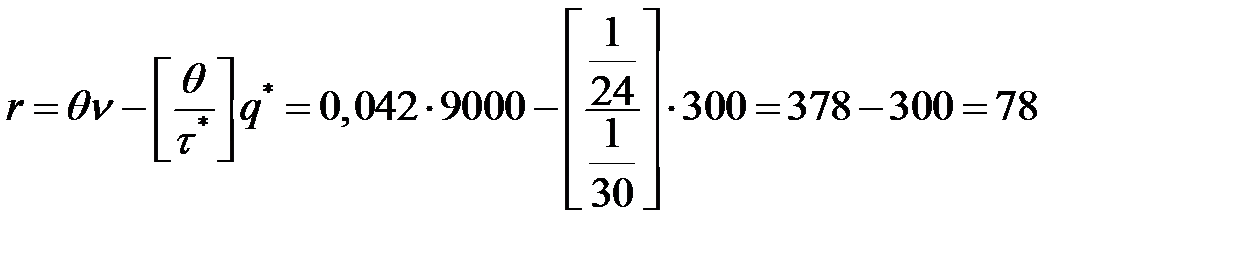 (тонн).
(тонн).
Минимальный начальный запас, гарантирующий бездефицитную работу предприятия, равен:
 (тонн).
(тонн).
Моменты размещения заказов (повторения заказов):
 ; t1=12 дней; t2=24 дня, …
; t1=12 дней; t2=24 дня, …
Минимальные среднегодовые издержки на размещение заказов и содержание запасов составят:
 (ден. ед.).
(ден. ед.).
График динамики изменения уровня запаса и фиктивного уровня запаса при  (
(  ), представлен на рисунке 10.5.
), представлен на рисунке 10.5.
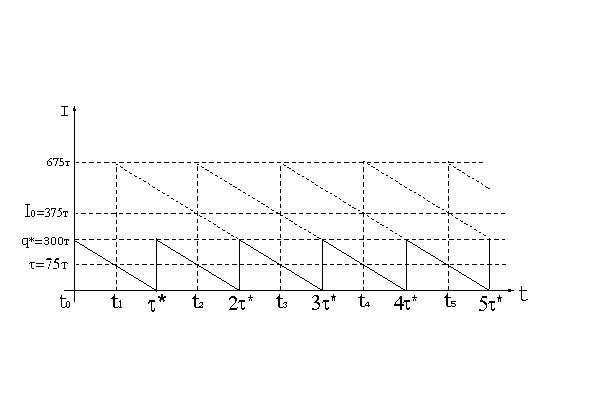
Рисунок 10.5
Из графика видно, что в интервале (  ) два заказа не выполнено, а в интервале
) два заказа не выполнено, а в интервале 
 не выполнен один заказ. В интервале
не выполнен один заказ. В интервале  величина заказанного сырья равна
величина заказанного сырья равна  т, а в интервале
т, а в интервале  - q*=300. Средний объем потребности в сырье равен
- q*=300. Средний объем потребности в сырье равен 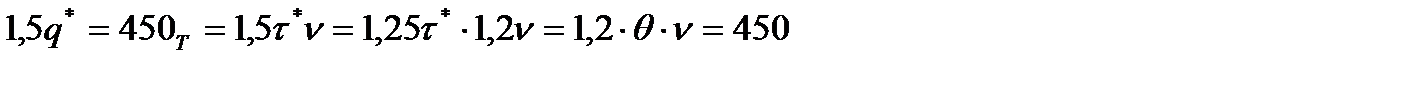 т, что больше величины потребности в сырье за время реализации заказа. Средний уровень фиктивной потребности в сырье равен:
т, что больше величины потребности в сырье за время реализации заказа. Средний уровень фиктивной потребности в сырье равен:

 (тонн).
(тонн).
10.2.4 Учет дискретности спроса 
Ранее мы предполагали, что спрос  является непрерывной величиной. В действительности же требования дискретны. Тогда оптимальная партия поставки
является непрерывной величиной. В действительности же требования дискретны. Тогда оптимальная партия поставки  должна быть целочисленной величиной и ее можно найти из условий:
должна быть целочисленной величиной и ее можно найти из условий:
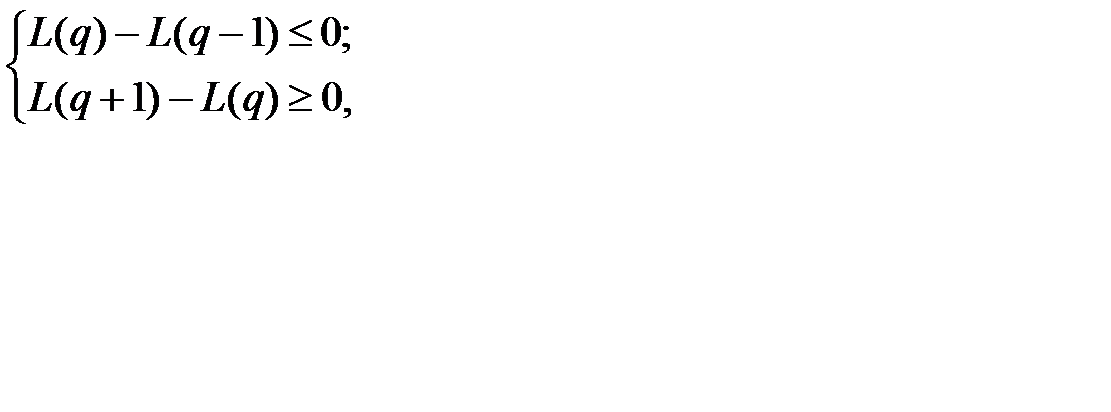
поскольку L(q*) принимает минимальное значение при  (см. график).
(см. график).
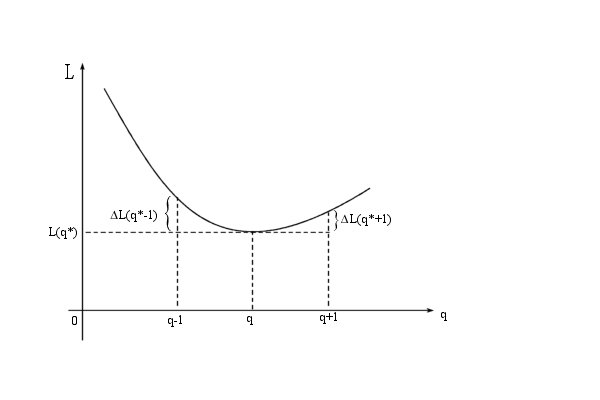
График функции L=L(q)
Подставив значение  , получим систему неравенств:
, получим систему неравенств:
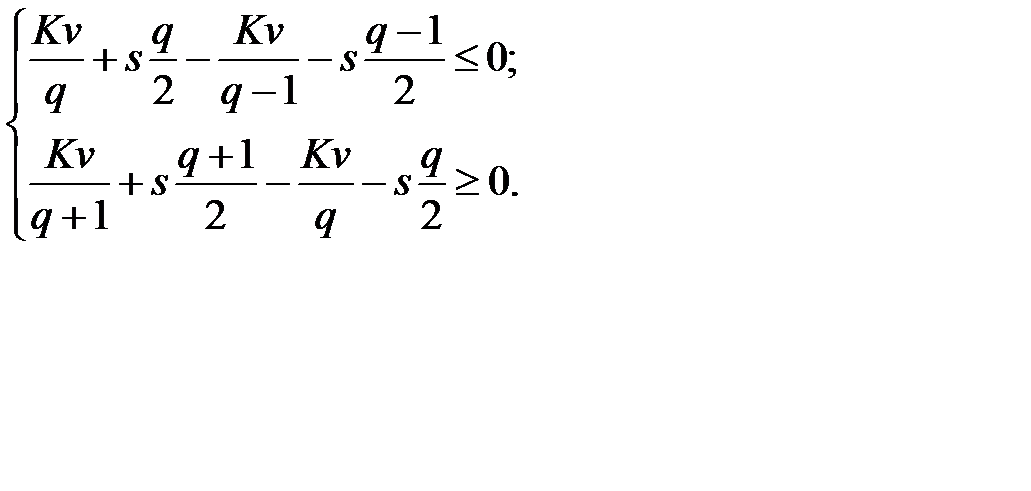
Решив систему относительно  , находим:
, находим:
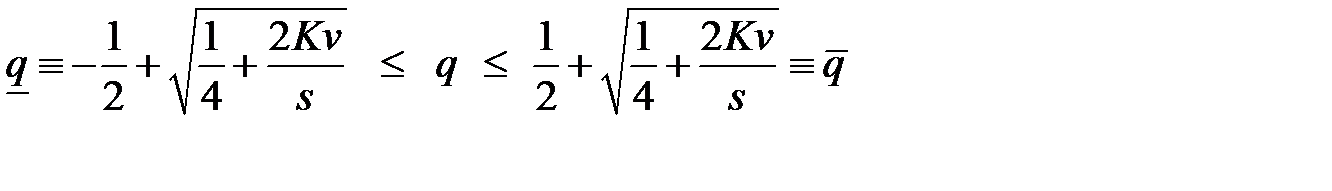 (10.3)
(10.3) 
Учитывая, что  , получим
, получим  (где
(где  - целая часть числа) для случая, когда
- целая часть числа) для случая, когда  и
и  не натуральные числа. Если
не натуральные числа. Если  и
и  , то оптимальных решений два:
, то оптимальных решений два:  и
и  .
.
Зная оптимальную партию поставки, находим оптимальный интервал возобновления заказа 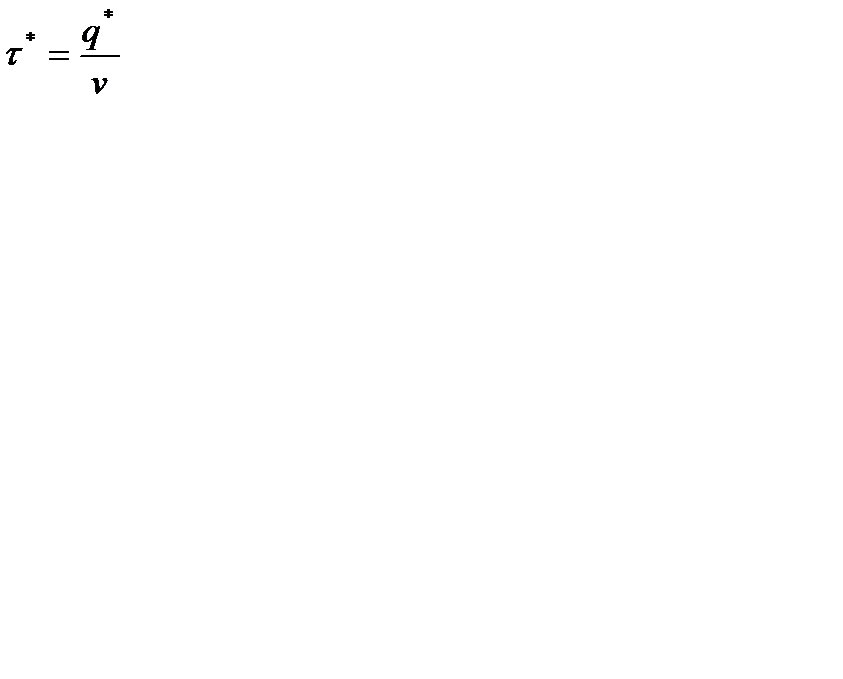 , который может быть не целочисленный. Поэтому выразим функцию издержек
, который может быть не целочисленный. Поэтому выразим функцию издержек  через
через  и составим систему неравенств для определения
и составим систему неравенств для определения  . Последовательно получаем
. Последовательно получаем
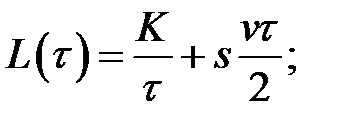
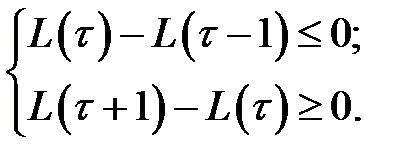
Решая систему, определяем неравенство для  :
:

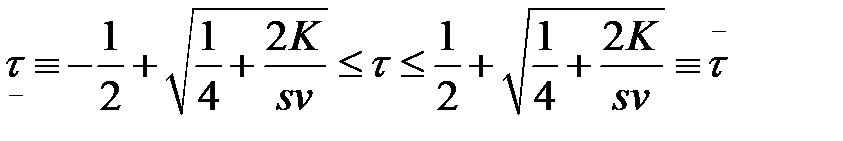
Из этого неравенства находим или одно оптимальное значение 
 (
(  - целая часть числа) или два оптимальных решения
- целая часть числа) или два оптимальных решения  и
и 
 , если
, если  и
и  .
.
Пусть  - время реализации заказа,
- время реализации заказа,  - оптимальный целочисленный период возобновления заказа,
- оптимальный целочисленный период возобновления заказа,  - число циклов, вмещающихся на промежутке
- число циклов, вмещающихся на промежутке  . Тогда точка размещения заказа будет вычисляться по формуле:
. Тогда точка размещения заказа будет вычисляться по формуле:
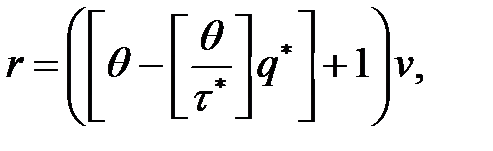
а моменты повторения заказа, по формуле:
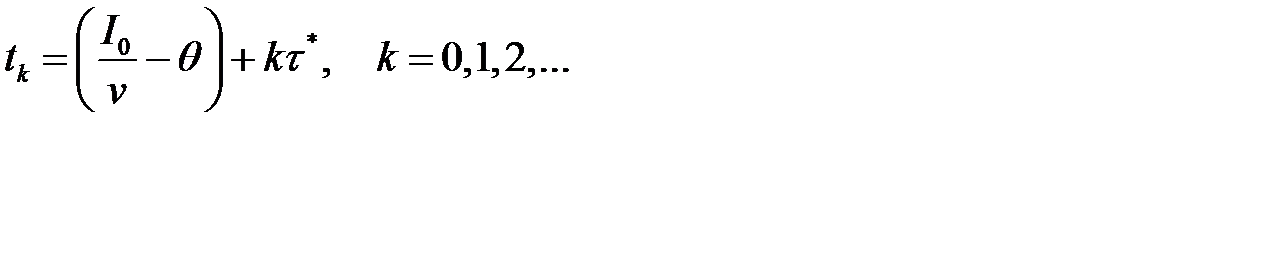
где  – фактический наличный начальный запас,
– фактический наличный начальный запас, 
Пример 10.2. Завод поставляет заказчику станки. Средняя потребность – 2 станка в год. Стоимость организации заказа К = 30 ден. ед. Издержки содержания, включая потери от иммобилизации средств в заказах s = 10 ден. ед. в год за один станок. Определить оптимальную партию поставки, оптимальный цикл, оптимальные издержки.
Решение. Поскольку станки – неделимая продукция, то воспользуемся формулой (9.3) для определения оптимальной партии поставки:
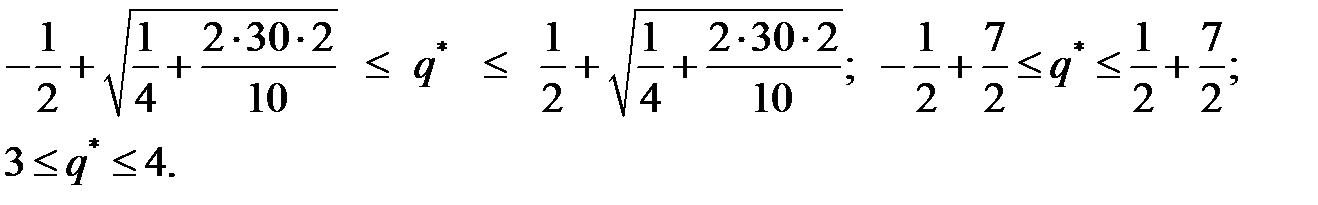
Следовательно, оптимальных решений два:  и
и  . При
. При  ,
,  (года),
(года),  При
При  ,
,  (года),
(года), 
Лекция 11 Экономико-математические методы и модели управления социально-культурной сферой (продолжение)
Вопросы, изучаемые на лекции:
11.1. Однопродуктовые детерминированные модели со статическим спросом (продолжение)
11.1.1. Модели с конечной интенсивностью поступления заказа
11.1.2. Модель с дефицитом, когда неудовлетворенные требования берутся на учет
11.1.3. Обобщенная модель оптимальной партии поставки с постоянной интенсивностью и с учетом неудовлетворенных требований
11.1.4. Модель в условиях скидки на размер заказа
Дата добавления: 2015-09-29; просмотров: 2068;
