Простейшая модель оптимального размера партии поставки (модель Уилсона)
Модель Уилсона основана на выборе такого фиксированного размера заказываемой партии, которая минимизирует расходы на заказываемый объем и содержание ресурса. Модель оптимальной партии поставки строится при следующих предположениях:
- уровень запаса снижается равномерно в соответствии с равномерно поступающими требованиями – спросом n.
- заказ выполняется мгновенно, т.е. время доставки равно нулю и уровень запаса восстанавливается до значения равного  .
.
- накладные расходы, связанные с размещением заказа и поставкой партии, не зависят от объема партии  и равны постоянной величине
и равны постоянной величине 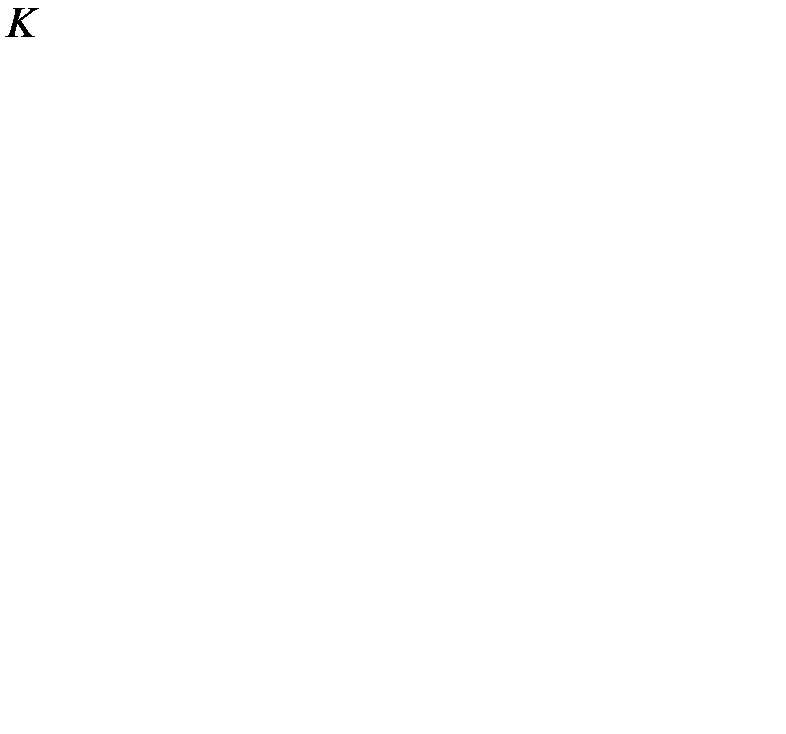 ;
;
- издержки содержания единицы продукции в единицу времени равны  .
.
Динамика изменения уровня запаса  в модели Уилсона представленная на рисунке 10.1. определяется следующим образом. Предположим, что в начальный момент времен уровень запаса
в модели Уилсона представленная на рисунке 10.1. определяется следующим образом. Предположим, что в начальный момент времен уровень запаса  равен
равен  . Затем в течение времени
. Затем в течение времени  уровень запаса равномерно снижается до 0, после чего подается заказ на доставку новой партии объема
уровень запаса равномерно снижается до 0, после чего подается заказ на доставку новой партии объема  . Заказ выполняется мгновенно и уровень запаса восстанавливается до величины
. Заказ выполняется мгновенно и уровень запаса восстанавливается до величины  .
.
0   2𝜏 2𝜏
|
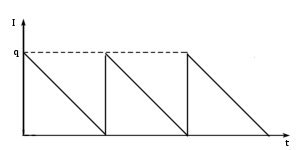
Рисунок 10.1
Интервал времени длиной  между поставками называется циклом. Очевидно, что
между поставками называется циклом. Очевидно, что 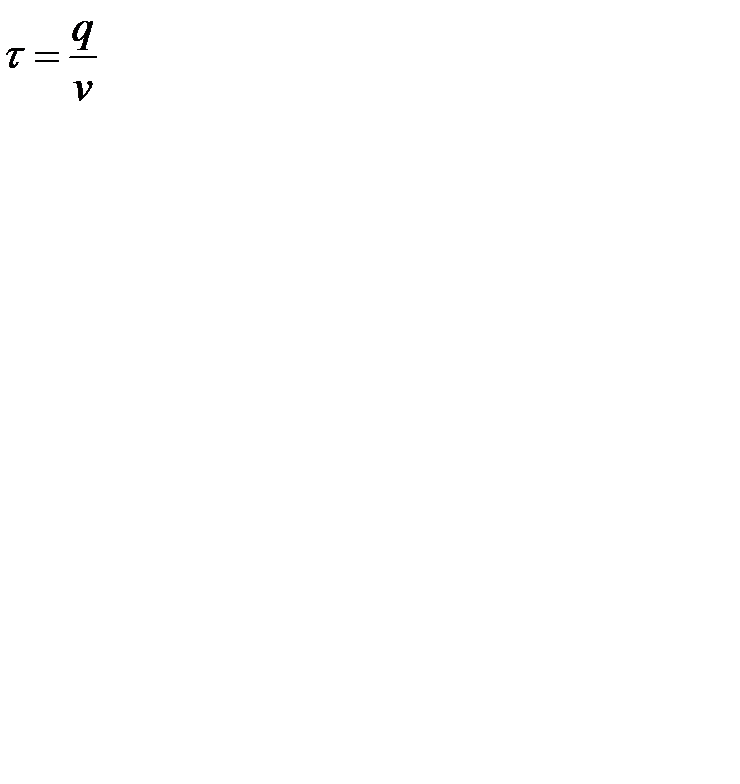 .
.
Затраты  в течение цикла
в течение цикла  состоят из накладных расходов
состоят из накладных расходов 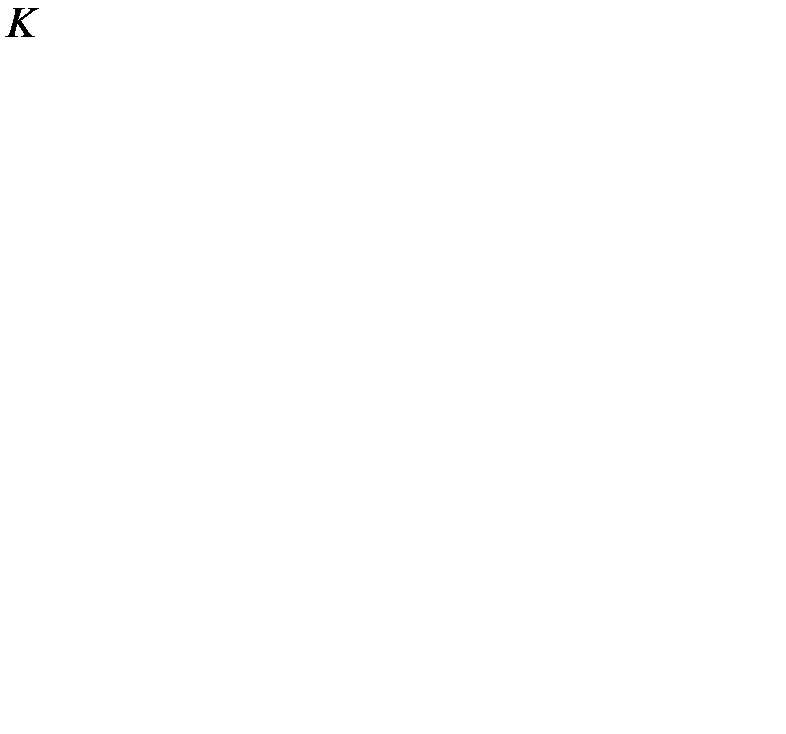 и издержек содержания запаса, которые пропорциональны средней величине текущего запаса
и издержек содержания запаса, которые пропорциональны средней величине текущего запаса  и времени содержания (длине цикла)
и времени содержания (длине цикла)  :
:


Разделив это выражение на длину цикла  , получим издержки в единицу времени:
, получим издержки в единицу времени:
 . (10.1)
. (10.1)
Издержки в единицу времени  являются функцией переменной
являются функцией переменной  . Поскольку издержки
. Поскольку издержки  должны быть минимальными, то найдем минимум функции
должны быть минимальными, то найдем минимум функции  . Для этого вычислим производную первого порядка и приравняем ее к нулю. Последовательно выполняя преобразования найдем стационарную точку.
. Для этого вычислим производную первого порядка и приравняем ее к нулю. Последовательно выполняя преобразования найдем стационарную точку.




 .
.
Так как  для всех
для всех  > 0, то
> 0, то
 (10.2)
(10.2)
точка минимума функции  . Следовательно, если объем партии равен
. Следовательно, если объем партии равен  , то издержки (10.1) при этом значении
, то издержки (10.1) при этом значении  достигают минимального значения. Формулу (10.2) называют формулой размера партии, экономичной величиной заказа, формулой квадратного корня или формулой Уилсона. Зная минимальный размер партии
достигают минимального значения. Формулу (10.2) называют формулой размера партии, экономичной величиной заказа, формулой квадратного корня или формулой Уилсона. Зная минимальный размер партии  , вычислим:
, вычислим:
- минимальный интервал между поставками

- минимальный средний уровень текущего запаса

- минимальные затраты по формированию заказа и содержанию запасов в единицу времени

- минимальное число поставок за период 
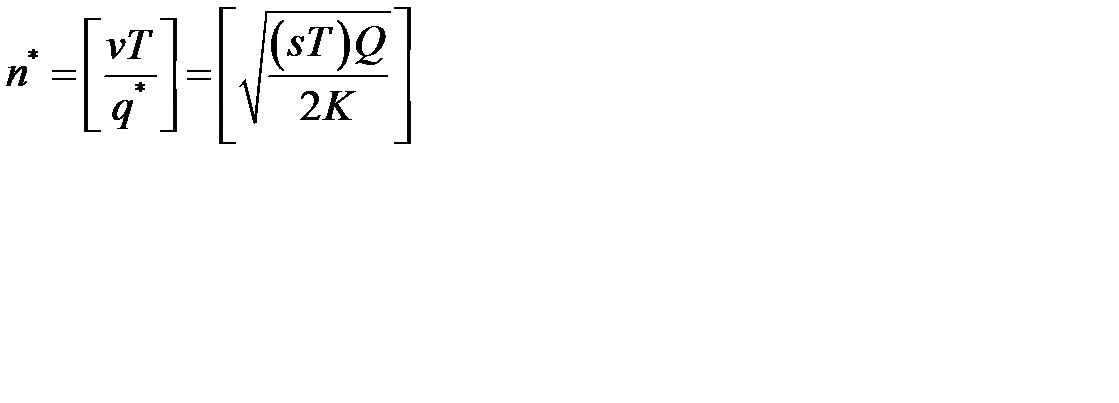 или
или  ,
,
где  =
=  – потребление за период
– потребление за период  ,
,  - наибольшее целое число, не превосходящее данное.
- наибольшее целое число, не превосходящее данное.
Если ввести в рассмотрение издержки размещения заказа в единицу времени  и средние издержки содержания запаса
и средние издержки содержания запаса  в единицу времени
в единицу времени  то минимальные затраты равны удвоенному среднему геометрическому из издержек размещения и содержания запаса:
то минимальные затраты равны удвоенному среднему геометрическому из издержек размещения и содержания запаса: 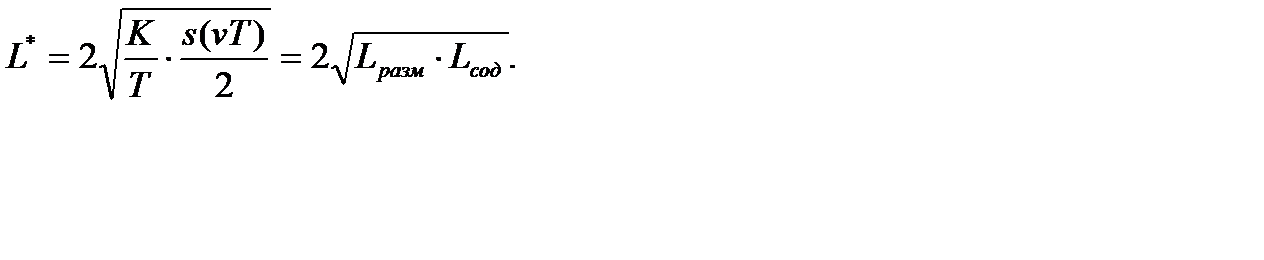
Если задана не интенсивность потребления  в единицу времени, а общий его объем запаса Q за период Т, то
в единицу времени, а общий его объем запаса Q за период Т, то 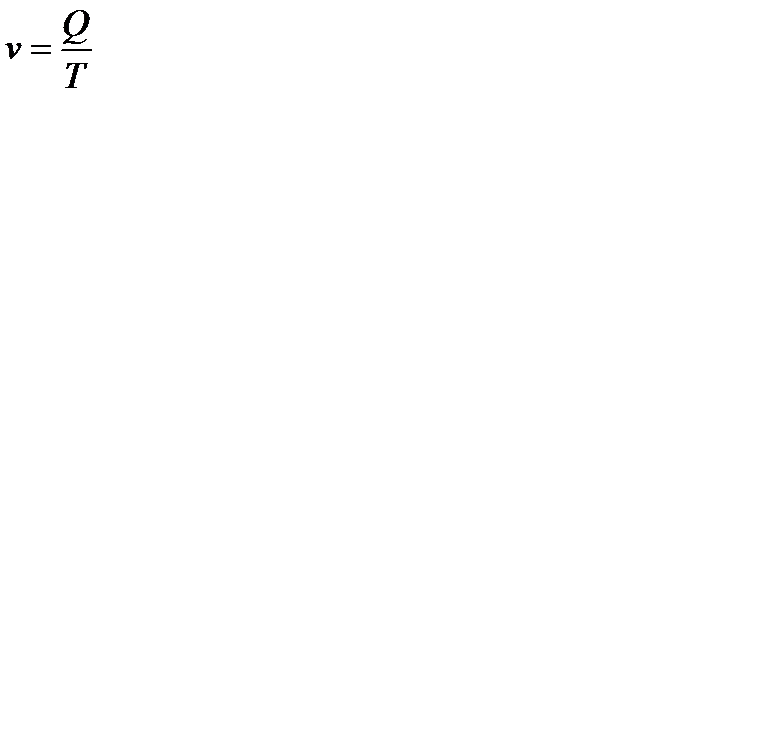 и тогда параметры модели Уилсона будут вычисляться по формулам:
и тогда параметры модели Уилсона будут вычисляться по формулам:
 ,
,  ,
, 
Модель Уилсона может быть использована при расчете оптимальной партии запуска продукции в производство. В этом случае величины, входящие в модель имеют другой смысл:
 - издержки, связанные с переналадкой оборудования, не зависящие от величины выпускаемой партии;
- издержки, связанные с переналадкой оборудования, не зависящие от величины выпускаемой партии;
 – величина партии запуска;
– величина партии запуска;
 - интенсивность потребления (например, годовая потребность в продукции);
- интенсивность потребления (например, годовая потребность в продукции);
s - издержки содержания единицы продукции в единицу времени. Издержки содержания при вычислении оптимальной партии запуска могут определяться величиной процента от стоимости единицы продукции  , т.е.
, т.е.  Параметры модели Уилсона выпуска продукции партиями будут вычисляться по формулам:
Параметры модели Уилсона выпуска продукции партиями будут вычисляться по формулам:
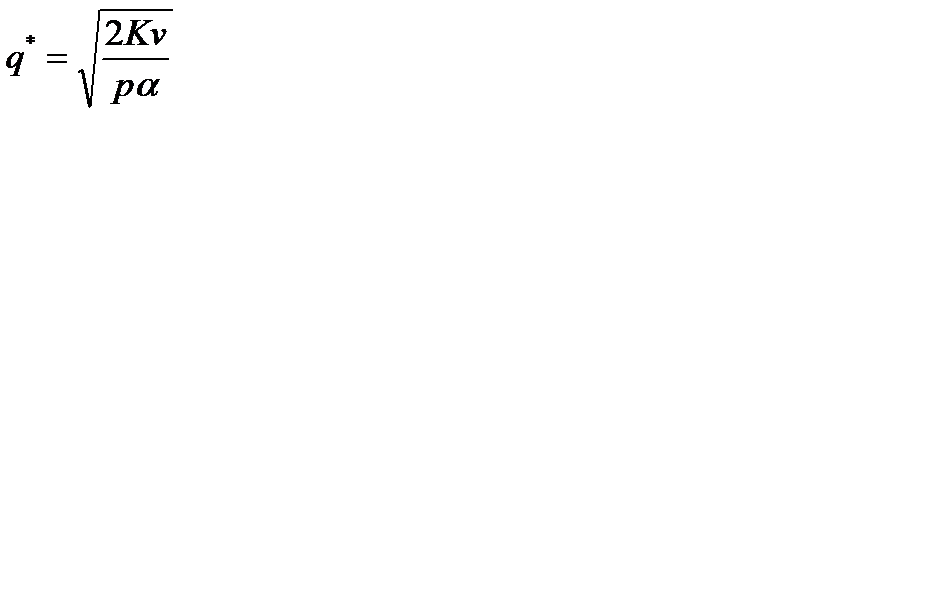 ;
; 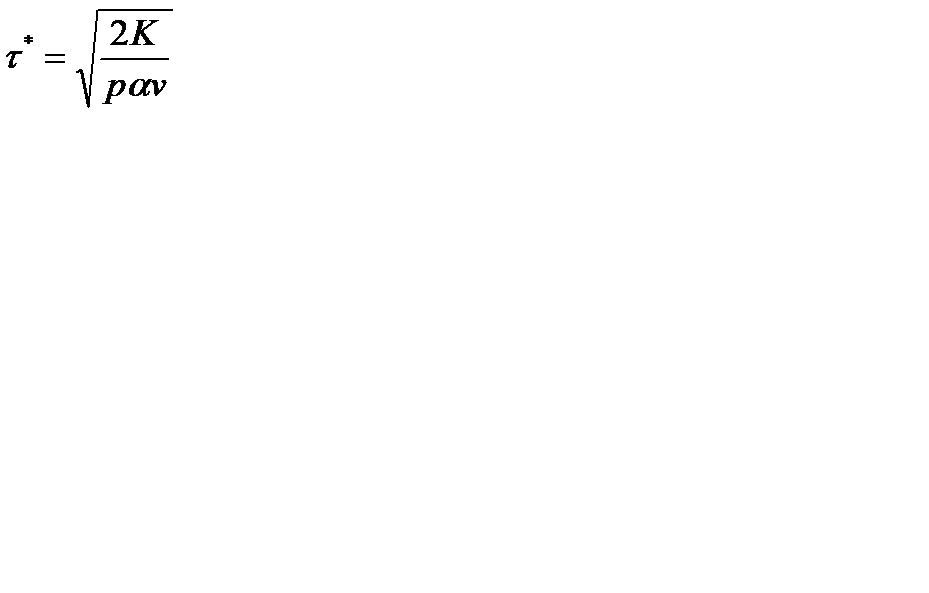 ;
;  .
.
Дата добавления: 2015-09-29; просмотров: 1444;
