Использование модели МОБ в исследовании взаимосвязи отраслевых структур валового выпуска и конечного спроса

Матричное уравнение , связывающее валовой выпуск отраслей (матрица ) и конечную продукцию (матрица ), является основным в межотраслевых моделях. Такая взаимосвязь позволяет решать как прямую задачу: определение объема и отраслевой структуры валового выпуска в зависимости от объема и отраслевой структуры конечной продукции; так и обратную: определение объема и отраслевой структуры конечного использования в зависимости от объема и отраслевой структуры валового выпуска.

При решении первой задачи предполагается, чтообъемы и отраслевая структура конечной продукции задана и что в прогнозном периоде не произойдет существенных технологических изменений по сравнению с отчетным периодом, т.е. технологическая матрица постоянная. Тогда из матричного уравнения находим объем и отраслевую структуру валового выпуска продукции:

.

Из этого уравнения можно определить, в какой степени изменение платежеспособного конечного спроса повлияет на объемы производства валовой продукции отраслей.

Если же будут заданы объемы и отраслевая структура валового выпуска, матрица , то, воспользовавшись уравнением

,

можно найти объемы и отраслевую структуру конечной продукции. Следовательно, можно найти, в какой степени спад производства в отдельных отраслях отразится в целом на величине конечного использования продукции отраслей и на валовом накоплении.

Оценку интенсивности влияния конечного спроса и технологических изменений на структурные сдвиги в экономике, т. е. на изменения в структуре валового выпуска, определяем из матричного уравнения: . Структурные сдвиги в экономике за период определим по формуле , используя следующую цепочку соотношений:

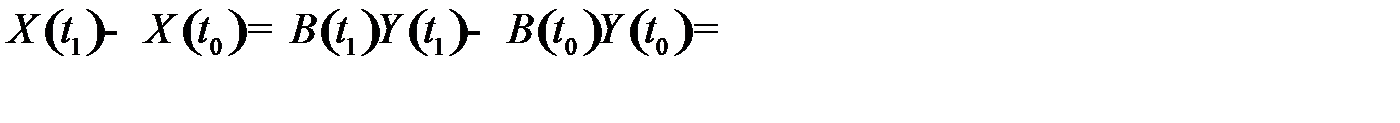
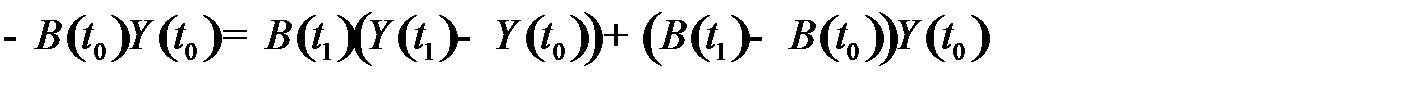, (9.1)

где и матрицы валовых выпусков отраслей;

и матрицы конечного спроса;

и матрицы коэффициентов полных затрат,

соответственно в периоды и .

Первое слагаемое формулы (9.1) определяет величину структурных сдвигов, обусловленных изменением конечного спроса; второе слагаемое определяет структурные сдвиги под влиянием технологических изменений. Для выявления реальных структурных изменений следует исключить из анализа воздействие ценового фактора.

Пример 9.1.Пустьматрица коэффициентов прямых затрат в модели Леонтьева равна: , а матрица-столбец конечного использования . Найти матрицу-столбец валового выпуска продукции и сформулировать экономическую интерпретацию коэффициентов прямых и полных затрат.

Решение. Для определения объема и структуры валового выпуска продукции воспользуемся формулой: , в которой неизвестной является матрица . Определим вначале матрицу 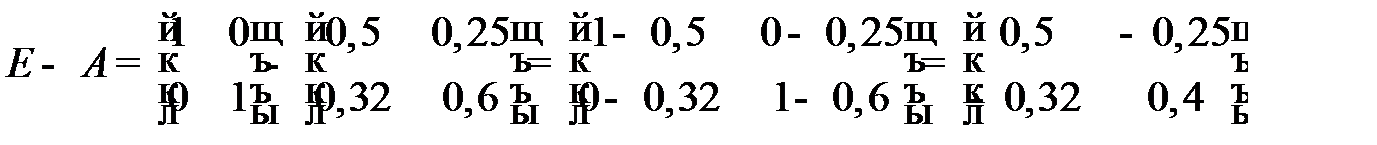и, применяя метод Гаусса, найдем обратную матрицу:

.

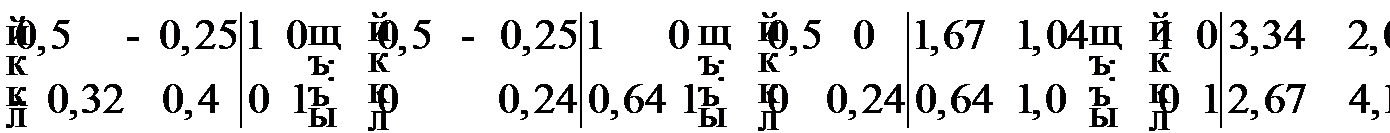Следовательно, .

Тогда объем и структура валового выпуска продукции определяется матрицей: .

Проанализируем значения коэффициентов матриц и с экономической точки зрения. Предположим, что данные отчетного МОБ измеряются в млрд. руб. Тогда:

- коэффициент матрицы означает, что для производства валовой продукции первой отрасли на сумму 1 млрд. руб., необходимо использовать объем валовой продукции первой отрасли на сумму 0,5 млрд. руб.;

- коэффициент матрицы означает, что для производства валовой продукции второй отрасли на сумму 1 млрд. руб., необходимо использовать объем валовой продукции первой отрасли на сумму 0,25 млрд. руб.;

- коэффициент матрицы означает, что для производства валовой продукции первой отрасли на сумму 1 млрд. руб., необходимо использовать объем валовой продукции второй отрасли на сумму 0,32 млрд. руб.; и т. д.

- коэффициент 3,32 матрицы означает, что для производства конечной продукции первой отрасли на сумму 1 млрд. руб., необходимо израсходовать валовой продукции первой отрасли на сумму 3,32 млрд. руб., так как коэффициенты полных затрат характеризуют совокупность прямых и косвенных затрат;

- коэффициент 2,08 матрицы означает, что для производства конечной продукции второй отрасли на сумму 1 млрд. руб., необходимо израсходовать валовой продукции первой отрасли на сумму 2,08 млрд. руб., и т. д.

Из экономической интерпретации коэффициентов и вытекают их некоторые свойства.

Показатель 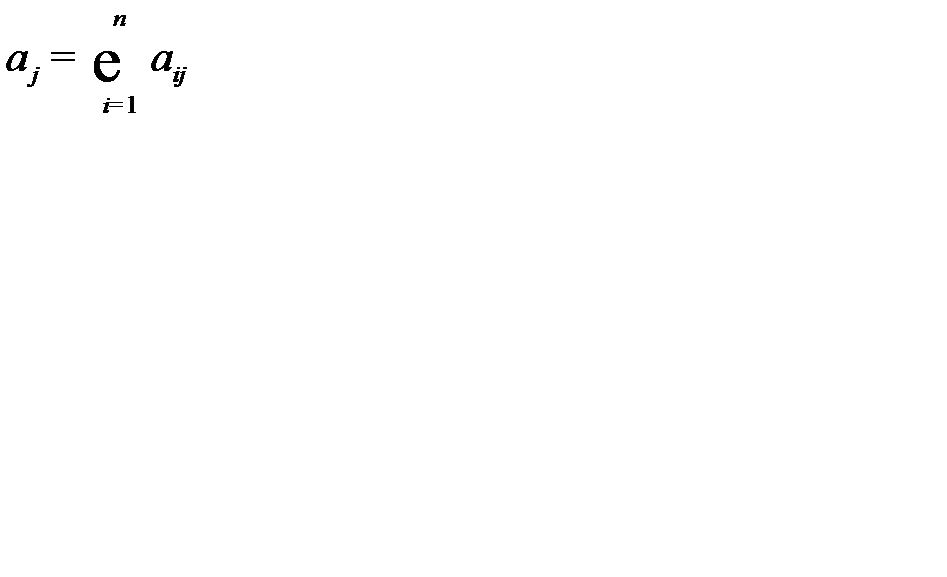определяет материалоемкость - той отрасли, а средневзвешенная материалоемкость отраслей , весами которых является валовая продукция отраслей , равна материалоемкости общественного продукта:

.

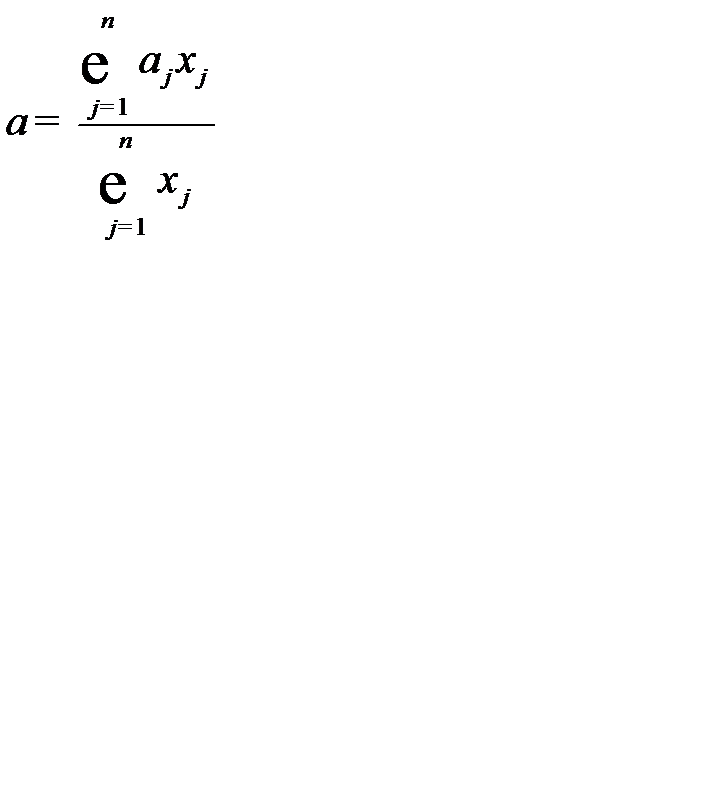Показатель 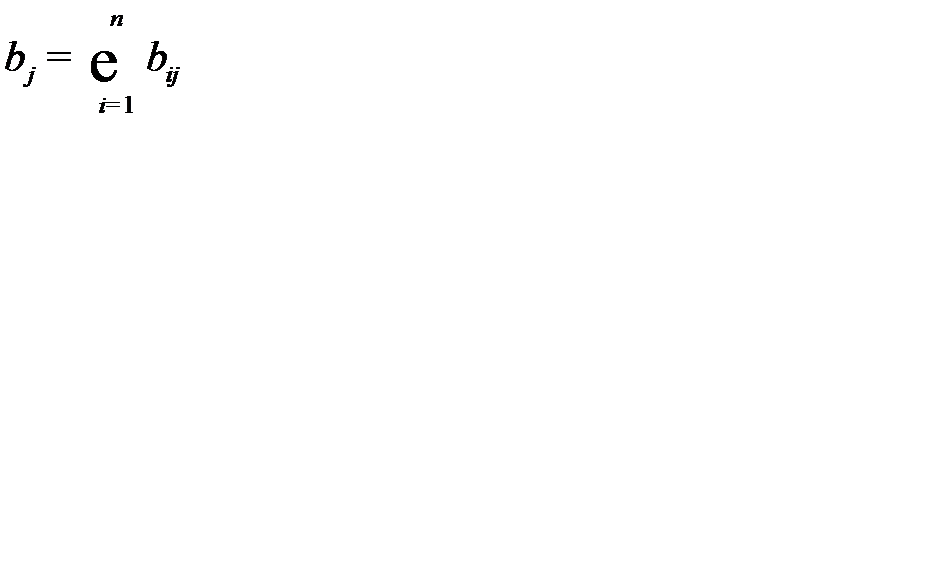определяет потребность в валовой продукции для получения единицы конечной продукции - той отрасли, а средневзвешенная потребность в валовой продукции , весами которой является объем конечной продукции, равна количеству валовой продукции, необходимой для производства единицы ВВП:

.

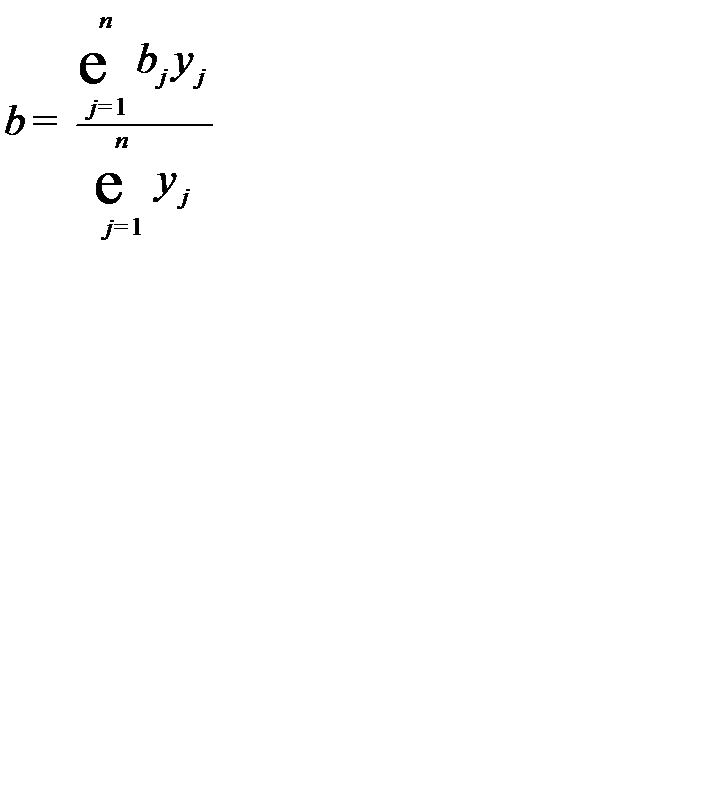Показатель характеризует соотношение ВВП и валовой общественной продукции.

Пример 9.2.Пусть задана матрица прямых затрат .

Определить конечное использование продукции каждой отрасли при условии, что валовой выпуск отраслей в прогнозном периоде в сопоставимых ценах (млрд. руб.) определяется матрицей .

Решение. Для определения объема и структуры конечного использования продукции воспользуемся уравнением , в котором неизвестной является матрица . Вычислив матрицу

=

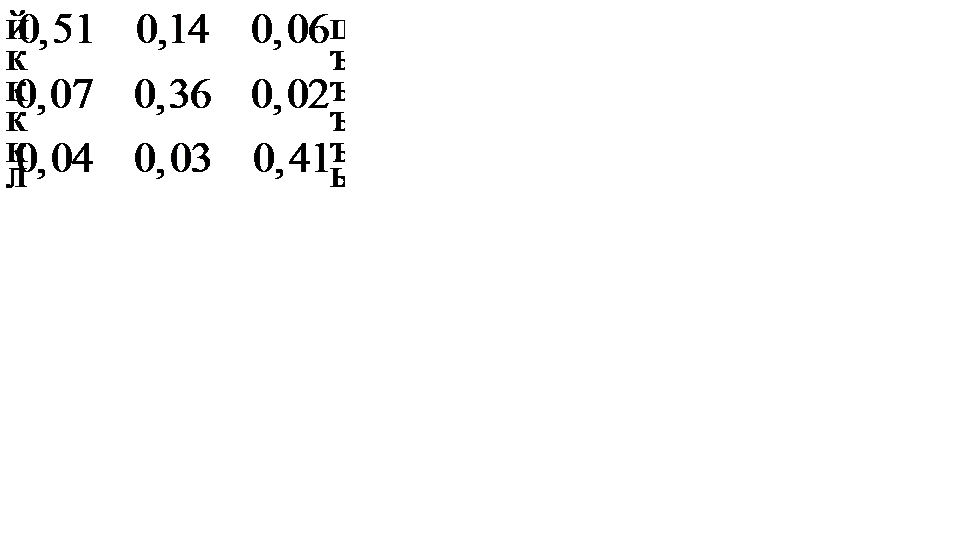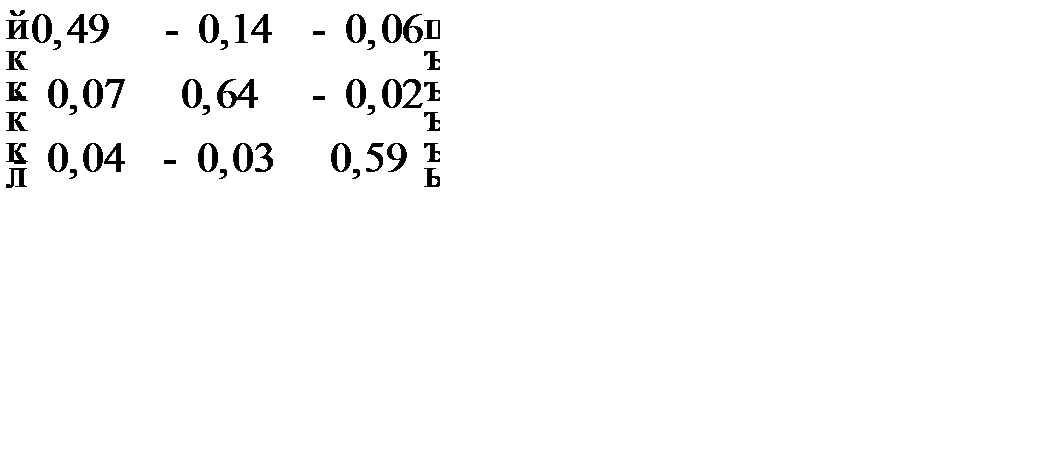
и воспользовавшись правилом умножения матриц, найдем конечное использование продукции отраслей в сопоставимых ценах (млрд. руб.):

= = .

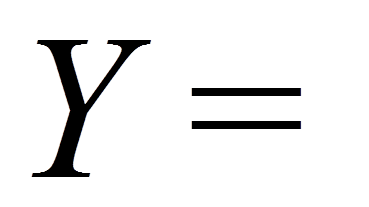
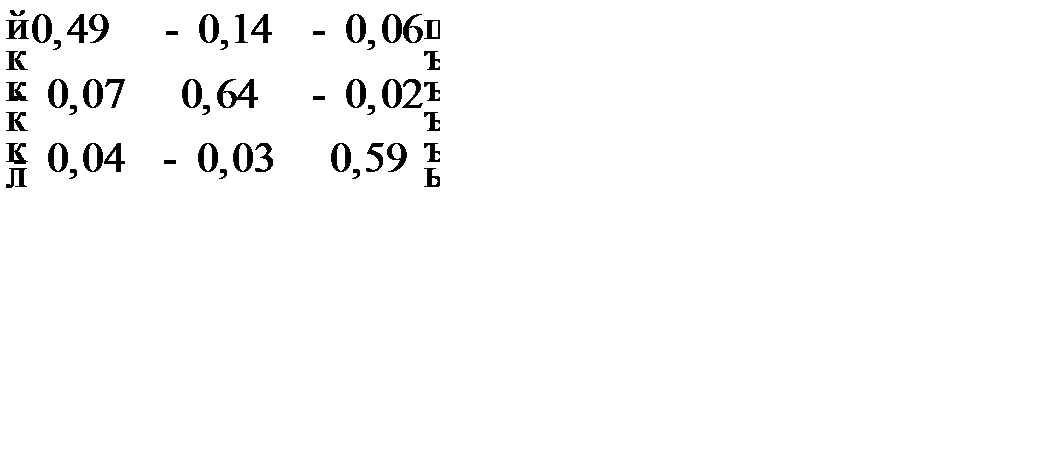
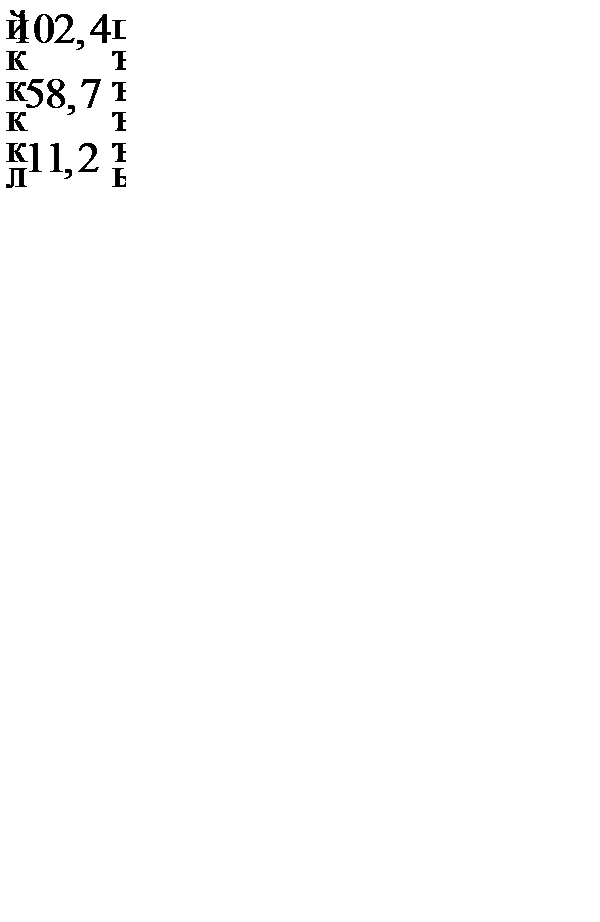Спрогнозировав конечное потребление (например, КП= 50 млрд. руб.) и сальдо экспорта-импорта (СЭИ= - 9 млрд. руб.) можно оценить валовое накопление (ВН) в рамках заданного валового выпуска: ВН= - КП – СЭИ= 41,286+30,176+0,751 - 50 + 9= 31,212(млрд. руб.).