Использование статической модели МОБ в прогнозировании цен
Прогнозирование цен осуществляется на основе первого и третьего квадрантов МОБ с использованием системы уравнений
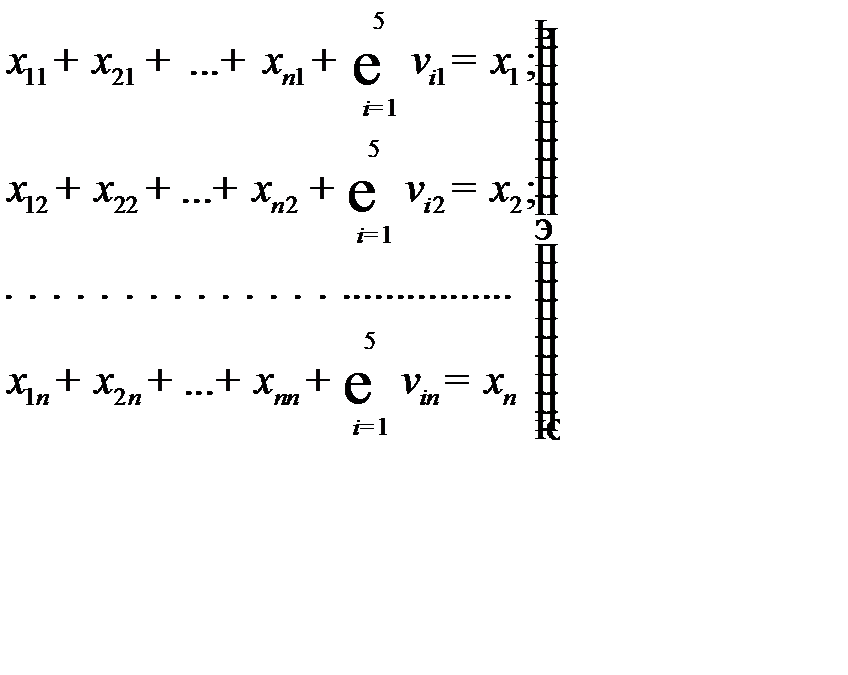 , (9.2)
, (9.2)
которая преобразуется, после подстановки  и деления на
и деления на  , в систему:
, в систему:
 . (9.3)
. (9.3)
Прогнозирование на период  осуществляется на основе данных МОБ предшествующего периода
осуществляется на основе данных МОБ предшествующего периода  . Структура затрат в сопоставимых ценах на рассматриваемом отрезке времени
. Структура затрат в сопоставимых ценах на рассматриваемом отрезке времени  предполагается неизменной. Пусть изменение цен в
предполагается неизменной. Пусть изменение цен в  -той отрасли характеризуется индексом цен
-той отрасли характеризуется индексом цен  , однако структура затрат в сопоставимых ценах осталась неизменной. При этих предположениях, элементы I и III квадрантов схемы МОБ запишутся как показано в таблице 9.1, поскольку элементы валовой добавленной стоимости являются составляющими цены.
, однако структура затрат в сопоставимых ценах осталась неизменной. При этих предположениях, элементы I и III квадрантов схемы МОБ запишутся как показано в таблице 9.1, поскольку элементы валовой добавленной стоимости являются составляющими цены.
Таблица 9.1
Схема первого и третьего квадрантов МОБ в текущих ценах
| Производящие отрасли | Потребляющие отрасли | |||
| … | n | |||

| 
| … | 
| |

| 
| … | 
| |
| … | … | … | … | |
| n | 
| 
| … | 
|
| Потребление основного капитала | 
| 
| … | 
|
| Заработная плата | 
| 
| … | 
|
| Прибыль | 
| 
| … | 
|
| Косвенные налоги | 
| 
| … | 
|
| Субсидии | - 
| - 
| … | - 
|
| Валовой выпуск | 
| 
| … | 
|
Как следует из систем (8.2) и (8.8), балансовые соотношения для прогнозирования цен примут вид:
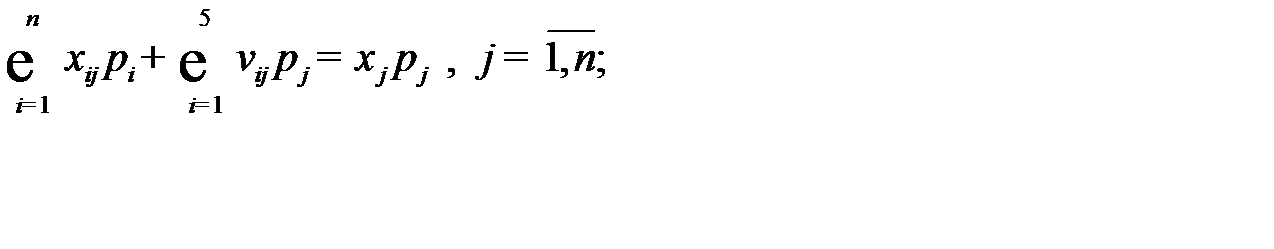 (9.4)
(9.4)
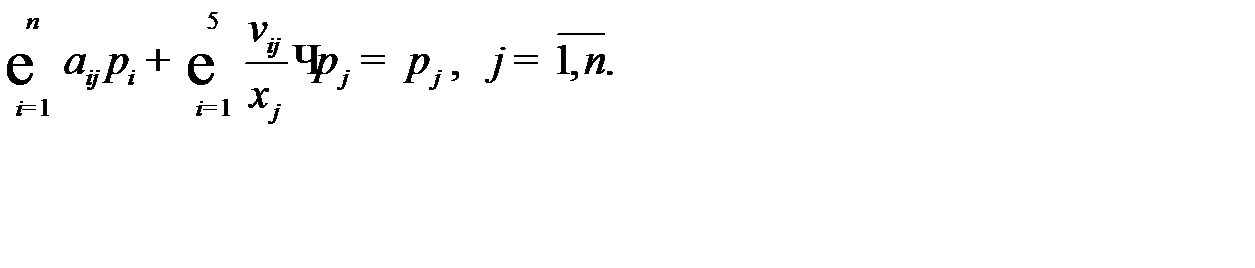 (9.5)
(9.5)
Системы (9.4) и (9.5) являются базовыми балансовыми моделями прогнозирования цен в отраслях экономики.
Пример 9.3.Пусть задана структура затрат последнего отчетного периода, представленная в таблице 9.2. Учитывая, что реальная динамика затрат в прогнозном периоде остается неизменной, оценить какое влияние оказывает увеличение цены на продукцию третьей отрасли в 5 раз на изменение цен в других отраслях.
Таблица 9.2.
Схема первого и третьего квадрантов трехотраслевого МОБ в текущих ценах
| Производящие отрасли | Потребляющие отрасли | |||
| 67,5 | 120,3 | 84,7 | ||
| 59,4 | 102,1 | 92,2 | ||
| 48,5 | 100,2 | 72,1 | ||
| Потребление основного капитала | 210,1 | 200,2 | 97,3 | |
| Заработная плата | 340,6 | 326,5 | 298,5 | |
| Прибыль | 91,1 | 49,4 | 56,3 | |
| Косвенные налоги | 46,2 | 50,1 | 41,1 | |
| Субсидии | -300 | -250 | -270 | |
| Валовой выпуск |
Решение. Поскольку структура затрат в прогнозном периоде остается неизменной, то увеличение цены на продукцию третьей отрасли в 5 раз приведет к увеличению цен на продукцию первой и второй отрасли в  и
и 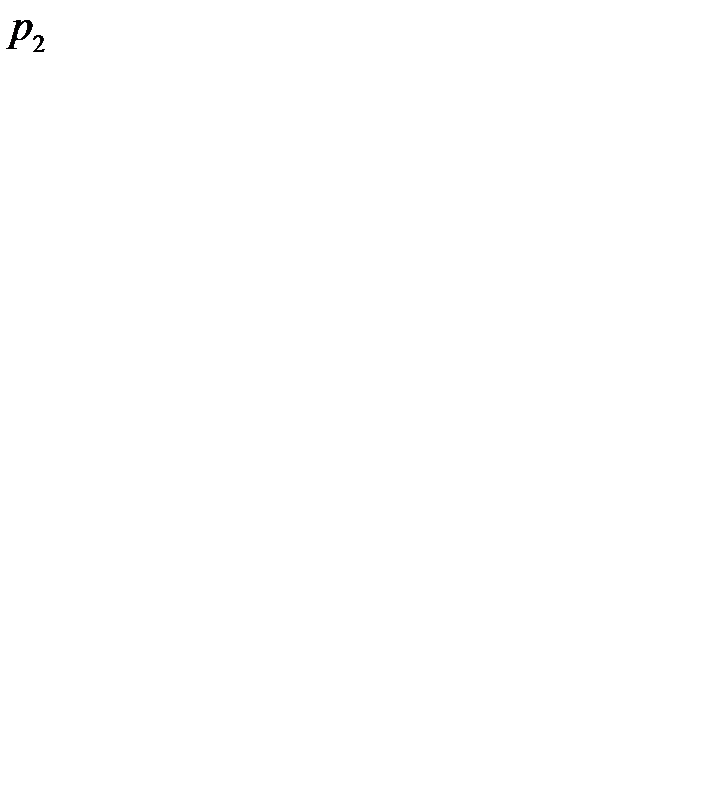 раз соответственно.
раз соответственно.
Из условия задачи следует, что задан индекс цен на продукцию третьей отрасли. Следовательно, величина затрат на продукцию третьей отрасли не влияет на формирование цены в этой отрасли. Для определения изменения цен в первой и второй отрасли составим систему вида (8.11). Она будет состоять из двух балансовых уравнений для первой и второй отрасли:

После приведения подобных членов, получим систему:

Для ее решения воспользуемся методом Гаусса. Составим расширенную матрицу системы и, применяя элементарные преобразования, приведем ее к виду, где слева от вертикальной черты будет записана единичная матрица:
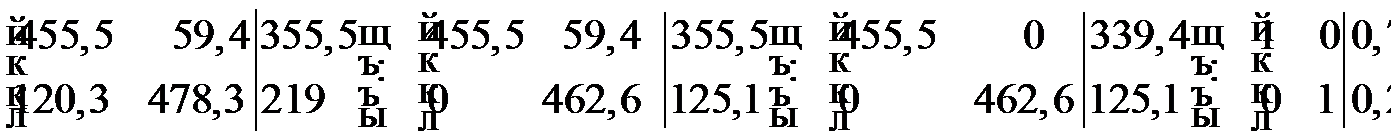 .
.
Тогда  и
и  . Таким образом, повышение цены на продукцию третьей отрасли в 5 раз приведет к повышению цены на продукцию первой отрасли в 0,74 раза, и второй отрасли – в 0,27 раза, при условии, что индекс роста цен всех элементов добавленной стоимости совпадает с индексом роста цен.
. Таким образом, повышение цены на продукцию третьей отрасли в 5 раз приведет к повышению цены на продукцию первой отрасли в 0,74 раза, и второй отрасли – в 0,27 раза, при условии, что индекс роста цен всех элементов добавленной стоимости совпадает с индексом роста цен.
Дата добавления: 2015-09-29; просмотров: 1307;
