Обобщенная модель оптимальной партии поставки с постоянной интенсивностью и с учетом неудовлетворенных требований
Рассмотрим модель с постоянной интенсивностью спроса  и постоянной интенсивностью поступления
и постоянной интенсивностью поступления  единиц в единицу времени. Предположим, что потери из-за дефицита сравнимы с издержками хранения. Тогда дефицит допускается, причем неудовлетворенные требования накапливаются и по мере новых поступлений удовлетворяются. Динамика изменения уровня запаса в этом случае показана на рисунке 11.5 и характеризуется следующими положениями:
единиц в единицу времени. Предположим, что потери из-за дефицита сравнимы с издержками хранения. Тогда дефицит допускается, причем неудовлетворенные требования накапливаются и по мере новых поступлений удовлетворяются. Динамика изменения уровня запаса в этом случае показана на рисунке 11.5 и характеризуется следующими положениями:
- в начальный момент времени уровень запаса равен нулю,  ;
;
- в течение времени  запас одновременно поступает и расходуется - это время накопления запаса;
запас одновременно поступает и расходуется - это время накопления запаса;
- в течение времени  запас только расходуется до нуля - это время расходования запаса;
запас только расходуется до нуля - это время расходования запаса;
- в течение времени  поступающие требования ставятся на учет - это время накапливания дефицита;
поступающие требования ставятся на учет - это время накапливания дефицита;
- в течение времени  поступает новая партия с интенсивностью
поступает новая партия с интенсивностью  и ликвидируется дефицит - это время ликвидации дефицита, затем идет накопления запаса и т. д.
и ликвидируется дефицит - это время ликвидации дефицита, затем идет накопления запаса и т. д.
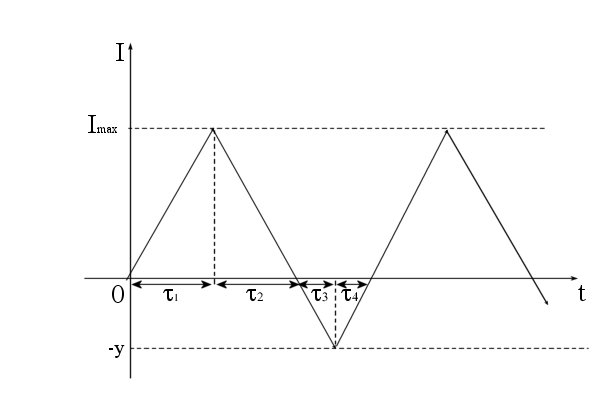
Рисунок 11.5
Пусть  величина партии поставки. Тогда
величина партии поставки. Тогда 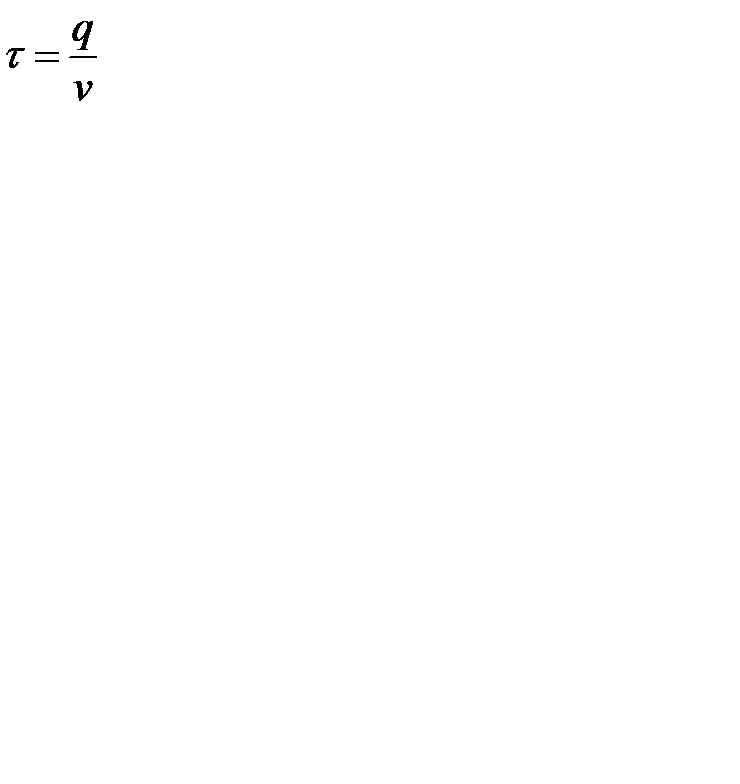 и
и  .
.
Пусть s – затраты содержания единицы продукции в единицу времени, а  - затраты дефицита единицы запаса в единицу времени. Из экономических соображений следует, что отношение максимального уровня наличного запаса к максимальной величине дефицита
- затраты дефицита единицы запаса в единицу времени. Из экономических соображений следует, что отношение максимального уровня наличного запаса к максимальной величине дефицита  равно отношению
равно отношению  к
к  , т.е.
, т.е. 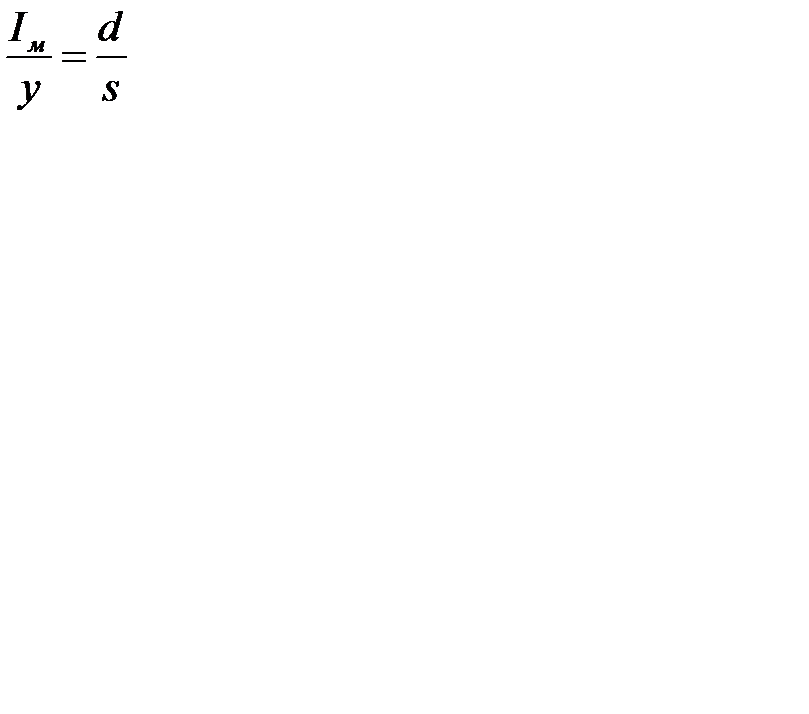 . Этому же отношению равно и отношение времени расходования запаса и времени накапливания дефицита. Максимальный уровень наличного запаса равен
. Этому же отношению равно и отношение времени расходования запаса и времени накапливания дефицита. Максимальный уровень наличного запаса равен  . Эта величина запаса полностью расходуется за время
. Эта величина запаса полностью расходуется за время  . Поэтому
. Поэтому  . Накопление максимальной величины дефицита идет со скоростью равной потреблению в течение времени
. Накопление максимальной величины дефицита идет со скоростью равной потреблению в течение времени  , т.е.
, т.е.  . Дефицит ликвидируется при поступлении новой партии со скоростью
. Дефицит ликвидируется при поступлении новой партии со скоростью  в течение времени
в течение времени  , т.е.
, т.е.  . Поэтому
. Поэтому  . Таким образом, получим систему из четырех уравнений, относительно
. Таким образом, получим систему из четырех уравнений, относительно  .
.
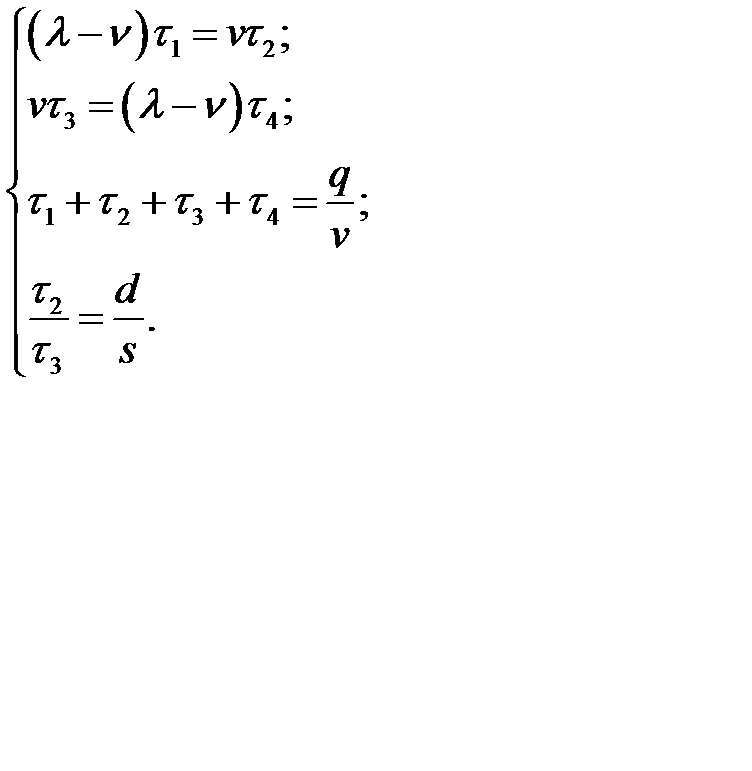
Решив систему относительно  , получим
, получим
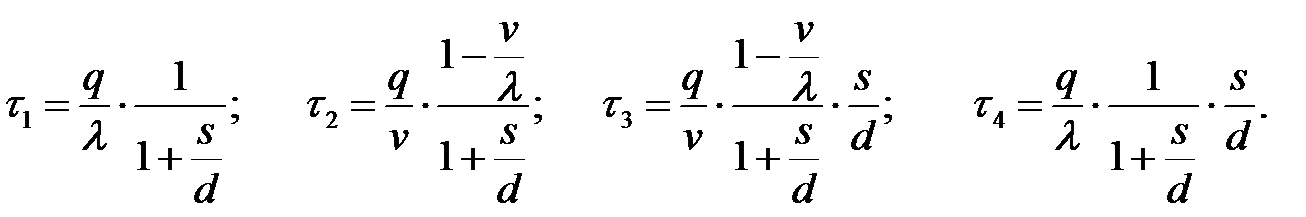
Издержки работы системы состоят из:
- издержек размещения заказа K, не зависящих от величины партии;
-издержек содержания запаса пропорциональных средней величине запаса 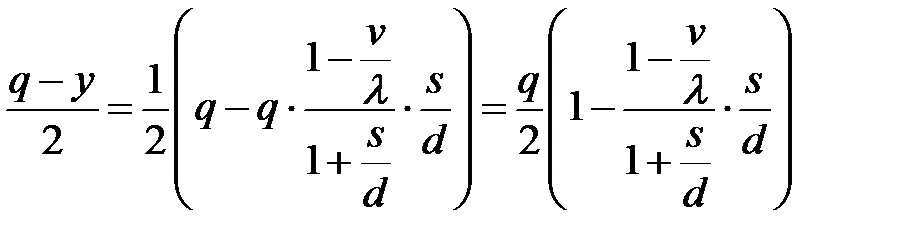 =
= 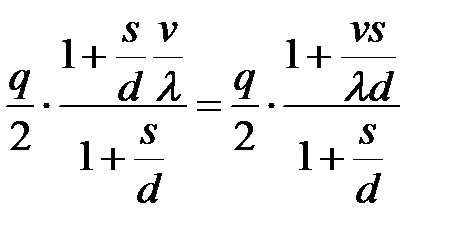
и времени его существования
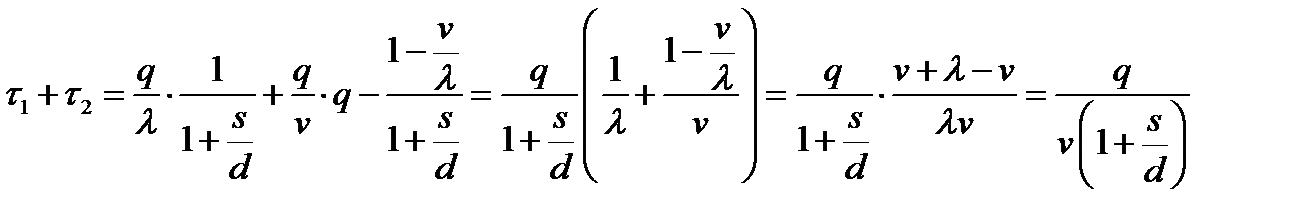 ;
;
- издержек от дефицита, пропорциональных средней величине дефицита
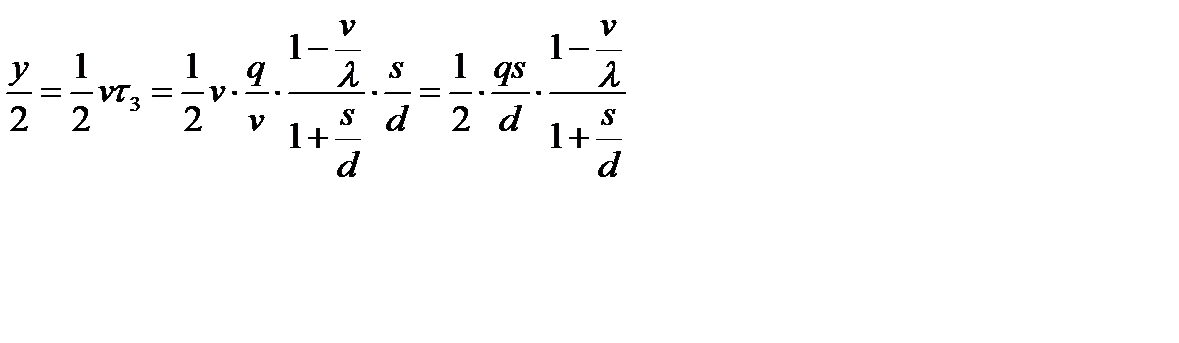
и времени его существования 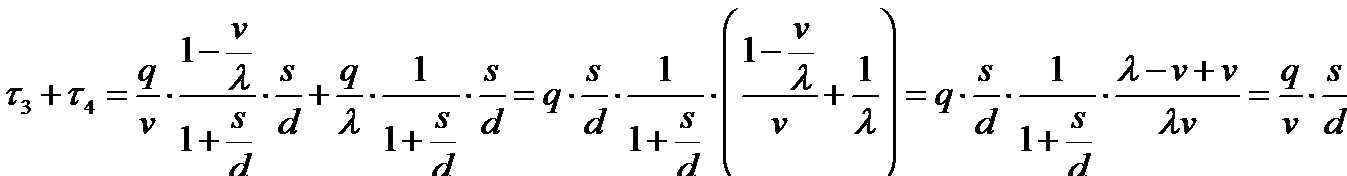
Тогда общие издержки в течение цикла равны сумме издержек от реализации заказа, содержания запасов и от дефицита:
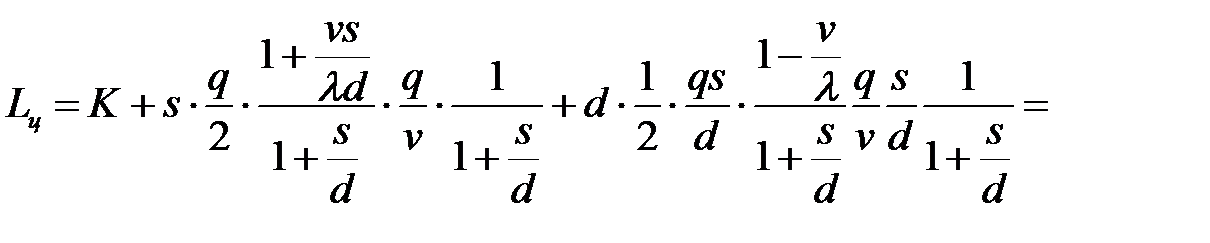
= 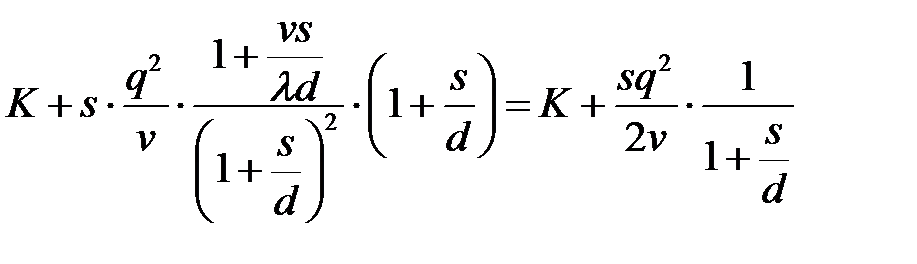
Разделив издержки цикла на величину цикла 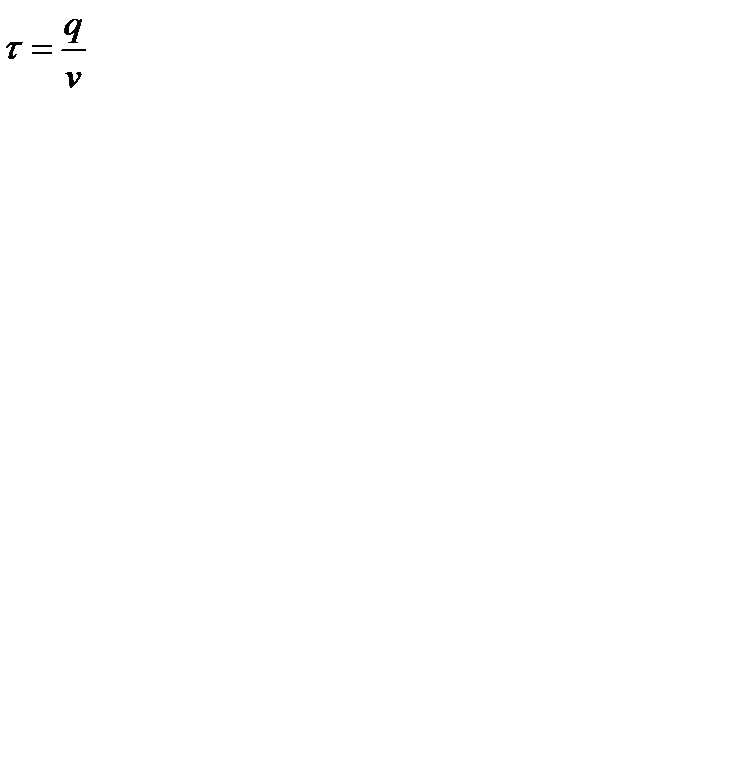 , получим издержки функционирования системы в единицу времени:
, получим издержки функционирования системы в единицу времени:
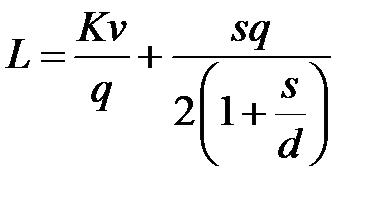 .
.
Это функция от величины  партии поставки
партии поставки  . Вычислим производную по
. Вычислим производную по  , приравняв ее к нулю, найдем
, приравняв ее к нулю, найдем  :
:
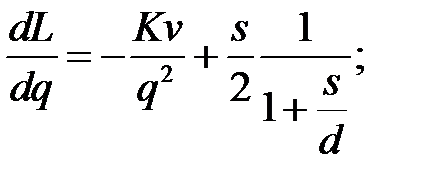
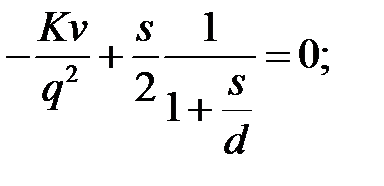
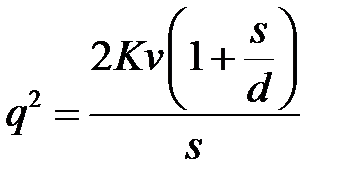 ;
; 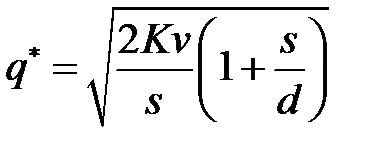 .
.
Это минимум функции  , так как
, так как  . Воспользовавшись найденным значением q*, находим:
. Воспользовавшись найденным значением q*, находим:
- максимальный уровень наличного запаса
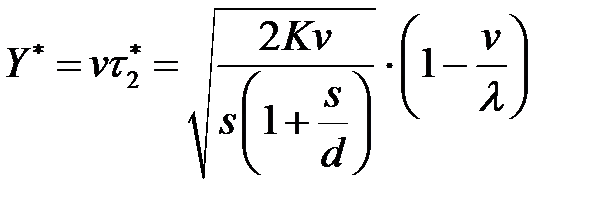
;
- максимальный уровень дефицита
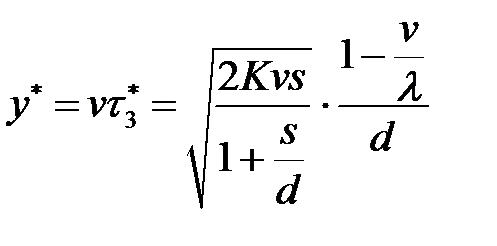 ;
;
- минимальный период возобновления заказа
 ;
;
- минимальные издержки функционирования системы в единицу времени
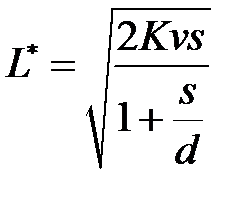 .
.
Пример 11.3. Фирма  выпускает партиями изделия пяти типов по 1500 штук в сутки. Средний объем потребления каждого типа изделия – 300 штук в сутки. Стоимость переналадки оборудования при переходе от одного типа изделия к другому составляет 1200 ден. ед. Стоимость содержания одного изделия 0,03 ден. ед. в сутки. Неудовлетворенные требования берутся на учет. Удельные издержки дефицита составляют 0,15 ден. ед. за изделие в сутки. Определить оптимальные параметры работы фирмы
выпускает партиями изделия пяти типов по 1500 штук в сутки. Средний объем потребления каждого типа изделия – 300 штук в сутки. Стоимость переналадки оборудования при переходе от одного типа изделия к другому составляет 1200 ден. ед. Стоимость содержания одного изделия 0,03 ден. ед. в сутки. Неудовлетворенные требования берутся на учет. Удельные издержки дефицита составляют 0,15 ден. ед. за изделие в сутки. Определить оптимальные параметры работы фирмы  .
.
Решение. В условии задачи заданы: интенсивность поступления  изделий в сутки; спрос
изделий в сутки; спрос  = 300 изделий в сутки; издержки переналадки оборудования
= 300 изделий в сутки; издержки переналадки оборудования 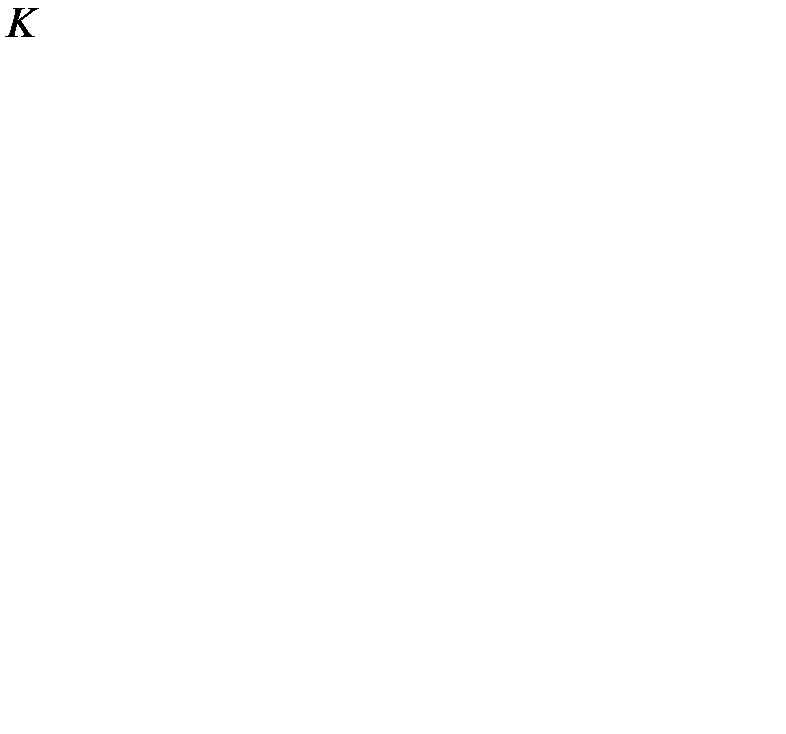 = 1200 ден. ед., издержки содержания s = 0,03 ден. ед. в сутки, издержки дефицита
= 1200 ден. ед., издержки содержания s = 0,03 ден. ед. в сутки, издержки дефицита  = 0,15 ден. ед. в сутки.
= 0,15 ден. ед. в сутки.
Воспользуемся моделью с постоянной интенсивностью поступления и спроса, когда неудовлетворенные поступления берутся на учет. Тогда минимальная партия поставки:
 (изделий);
(изделий);
- минимальный уровень наличного запаса:
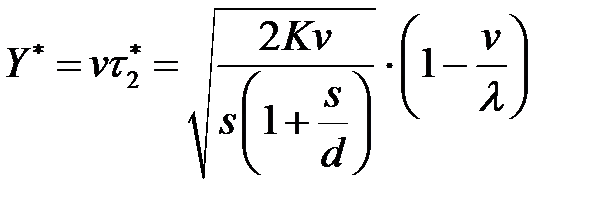 =
= 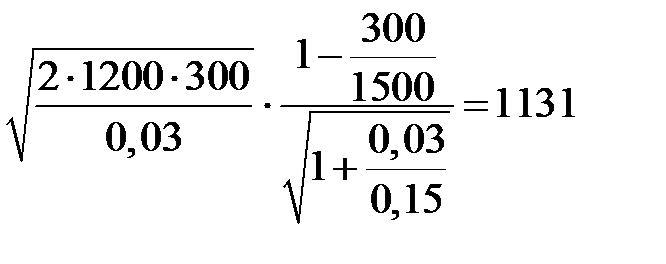 (изделий);
(изделий);
- максимальный уровень дефицита:
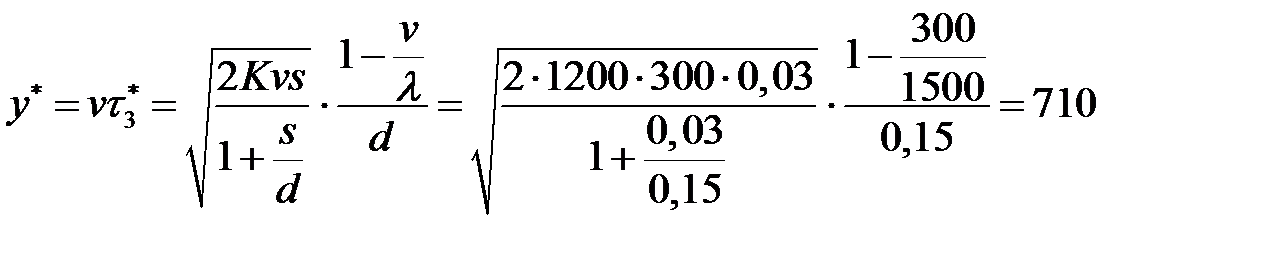 (изд.);
(изд.);
- минимальный период возобновления заказа:
 (суток);
(суток);
- время накопления и расходования:
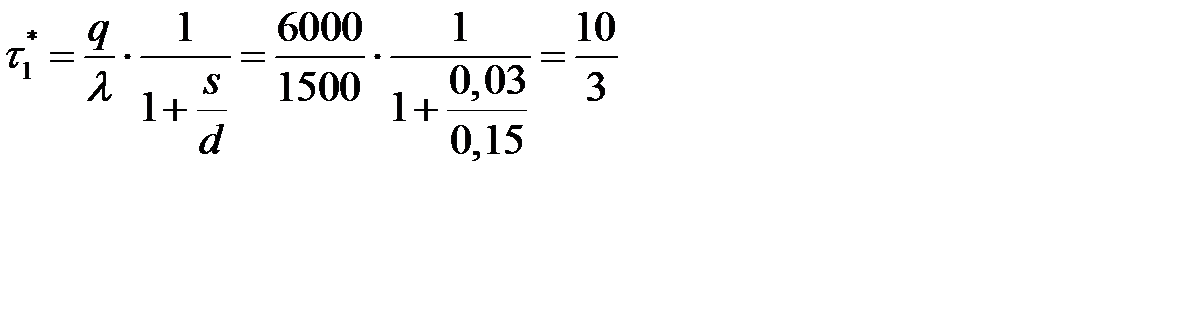 (суток);
(суток);
- время расходования:
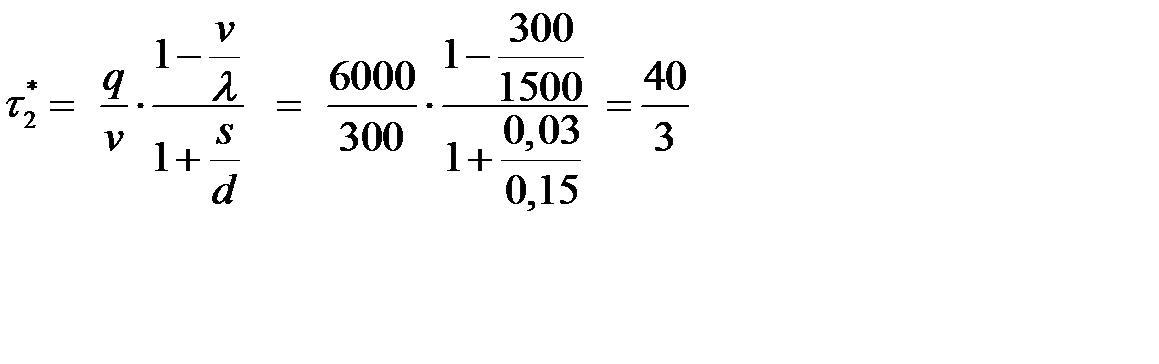 (суток);
(суток);
- время накопления дефицита:
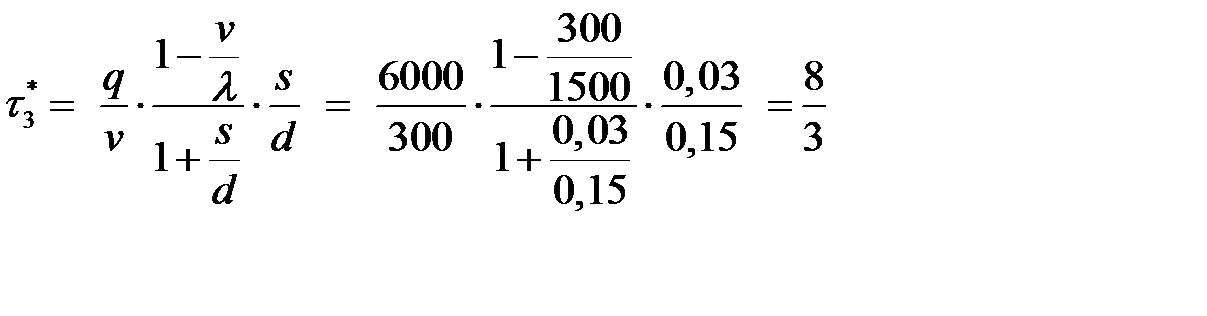 (суток);
(суток);
- время ликвидации дефицита:
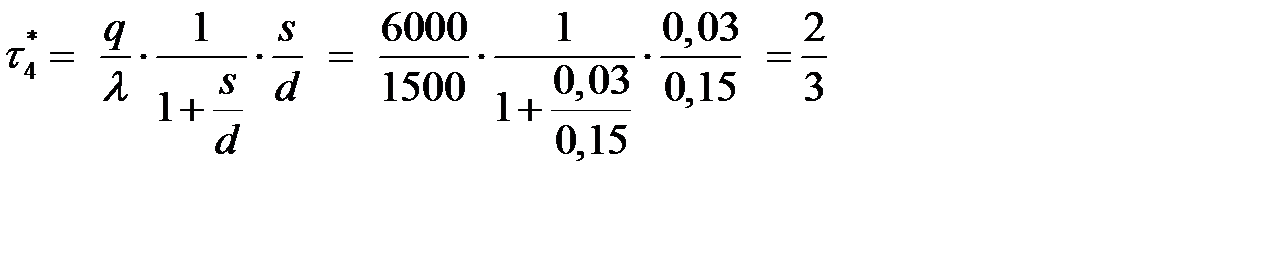 (суток).
(суток).
Условие 
 , выполняется.
, выполняется.
Минимальные издержки работы фирмы за сутки равны:
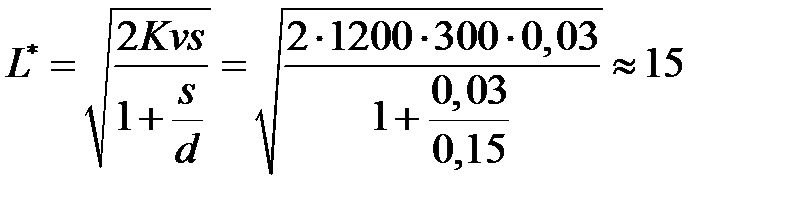 (ден. ед.)
(ден. ед.)
Время, которое необходимо на производство одной партии:
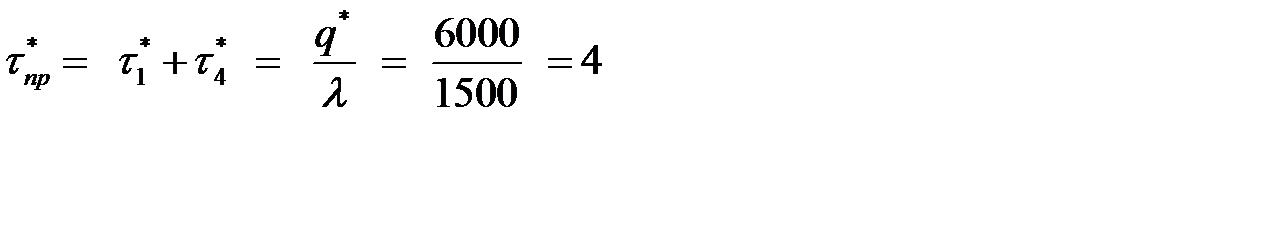 (суток).
(суток).
Так как  , то мощность фирмы позволяет наладить выпуск пяти типов изделий партиями по
, то мощность фирмы позволяет наладить выпуск пяти типов изделий партиями по  изделий.
изделий.
Дата добавления: 2015-09-29; просмотров: 1181;
