Однопериодная модель со случайным спросом
Поскольку на поступление продуктов, спрос на них, на время выполнения заказов оказывает влияние множество случайных факторов, вызывая их колебания, то эти величины являются случайными величинами. Так как определяющим фактором в моделях является спрос, то рассмотрим модели со случайным спросом.
Будем предполагать, что спрос на продукцию или расход материальных ресурсов является стационарной случайной величиной 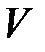 с математическим ожиданием
с математическим ожиданием 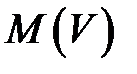 и конечной дисперсией
и конечной дисперсией 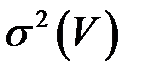 . Рассмотрим случай, когда спрос
. Рассмотрим случай, когда спрос 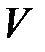 –дискретная случайная величина, заданна рядом распределения:
–дискретная случайная величина, заданна рядом распределения:

| 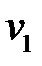
| 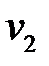
| 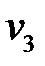
| … | 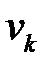
| … |
p(  ) )
| 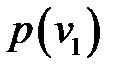
| 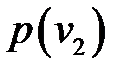
| 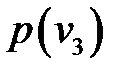
| … | 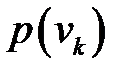
| … |
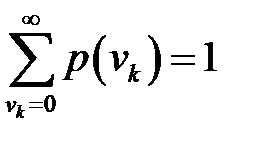 . Числовые характеристики этой случайной величины вычисляются по формулам:
. Числовые характеристики этой случайной величины вычисляются по формулам:
- математическое ожидание: 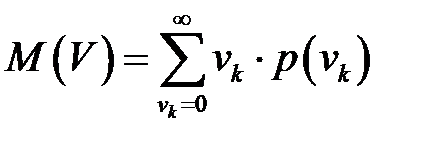 ;
;
- дисперсия: 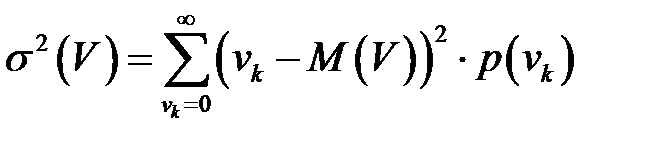 ;
;
- вероятность того, что спрос  не превысит величины
не превысит величины  - это сумма вероятностей:
- это сумма вероятностей:  .
.
Партия поставки продукции или партия запуска продукции в производство вычисляется при следующих предположениях:
 - покупная цена (или стоимость) единицы продукции;
- покупная цена (или стоимость) единицы продукции;
 (
(  ) - цена реализации неиспользованной продукции;
) - цена реализации неиспользованной продукции;
 - затраты на содержание единицы продукции в единицу времени;
- затраты на содержание единицы продукции в единицу времени;
 - издержки, связанные с дефицитом единицы продукции в единицу времени.
- издержки, связанные с дефицитом единицы продукции в единицу времени.
Функция издержек при случайном спросе определяется математическим ожиданием издержек функционирования системы и состоит из: издержек приобретения заказа, содержания запаса, дефицита, реализации неиспользованной продукции.
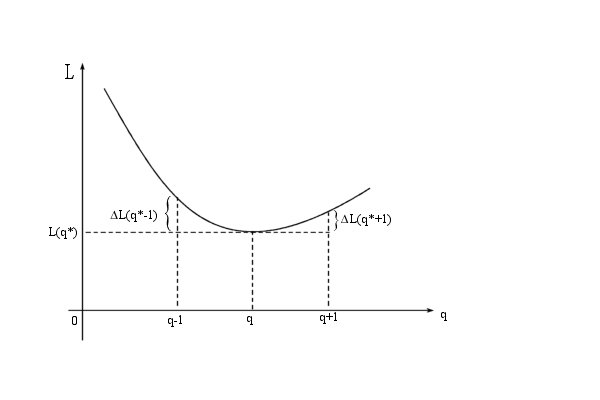
Рисунок 12.1
Поскольку функция издержек  системы унимодальная (см. рисунок 12.1), то оптимальной считаем такую величину заказа
системы унимодальная (см. рисунок 12.1), то оптимальной считаем такую величину заказа  , при которой математическое ожидание издержек функционирования системы минимально, т. е. должны выполняться неравенства:
, при которой математическое ожидание издержек функционирования системы минимально, т. е. должны выполняться неравенства:
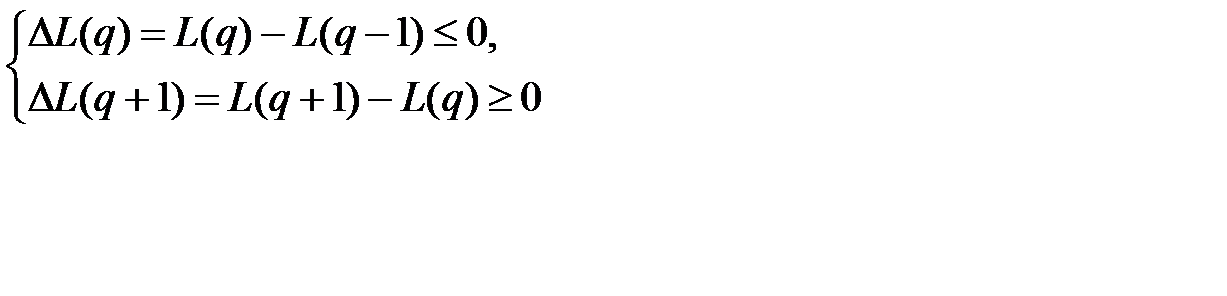 (12.16)
(12.16)
где 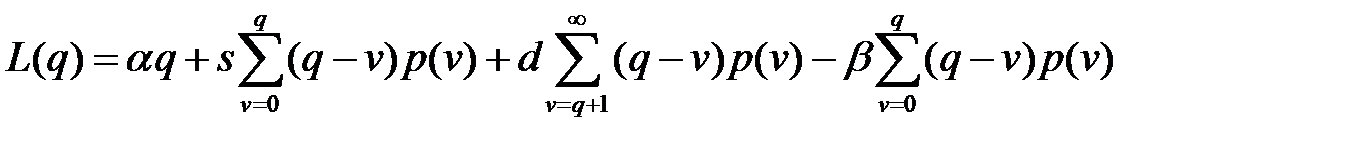 .
.
Так как 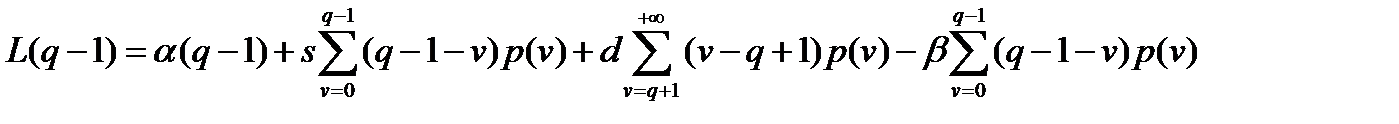 и
и
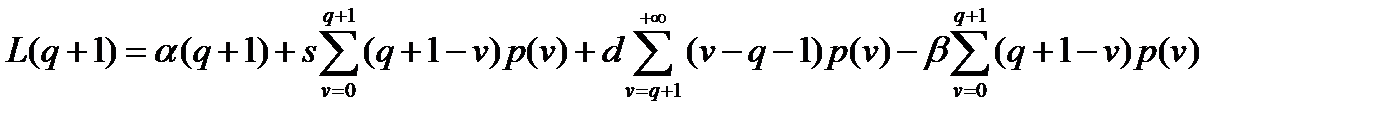 , то подставив эти значения в систему (12.16), получим:
, то подставив эти значения в систему (12.16), получим:
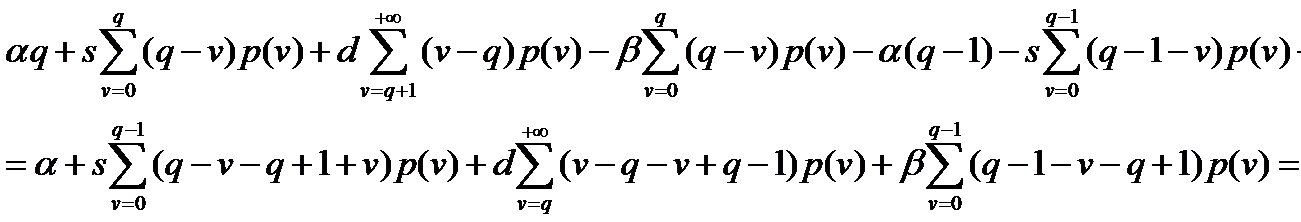
или
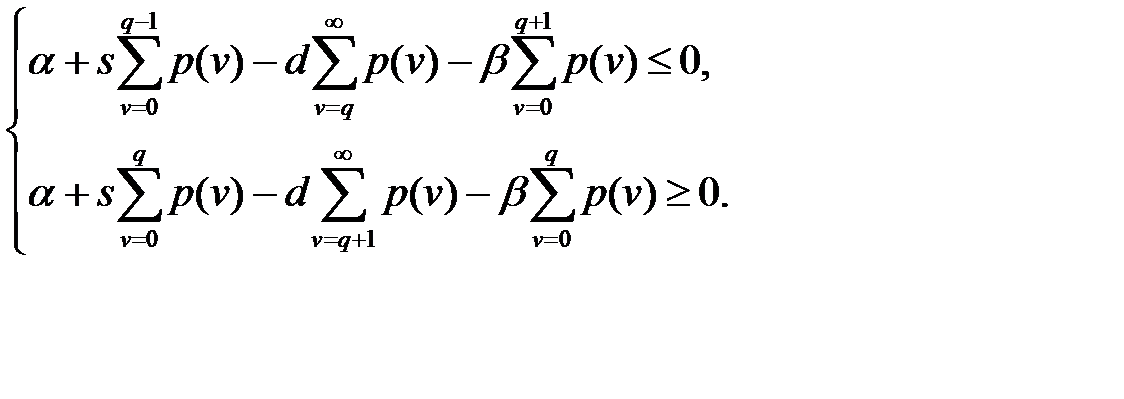
Так как 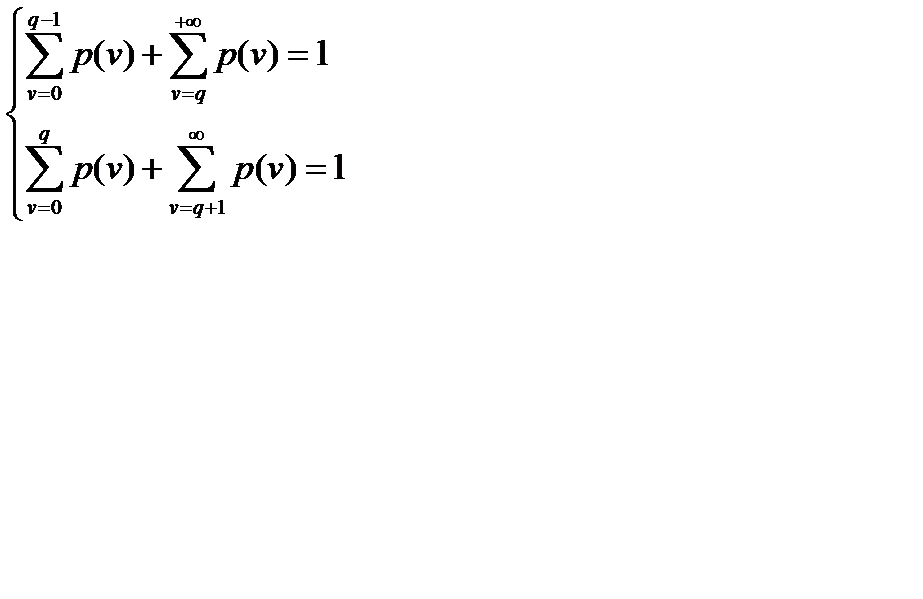 , то подставляя
, то подставляя 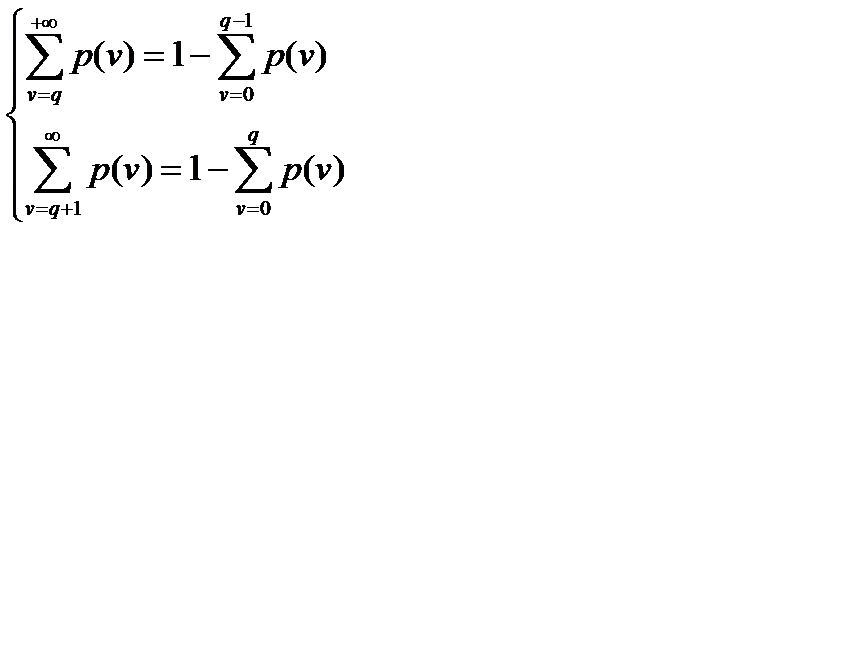 , получим систему:
, получим систему:
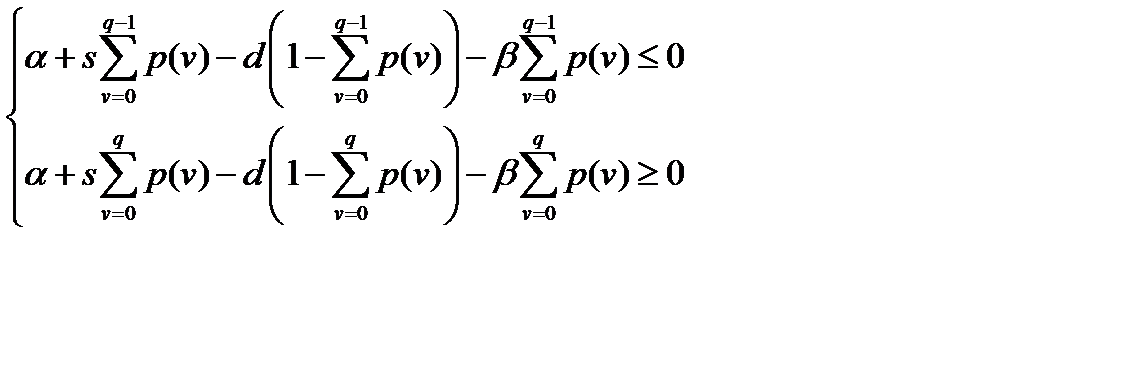 ,
, 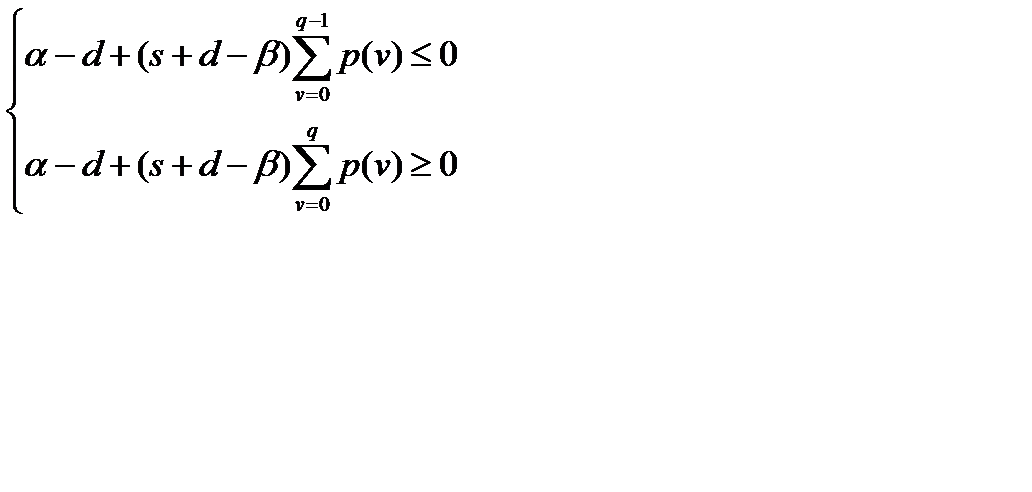 ,
,
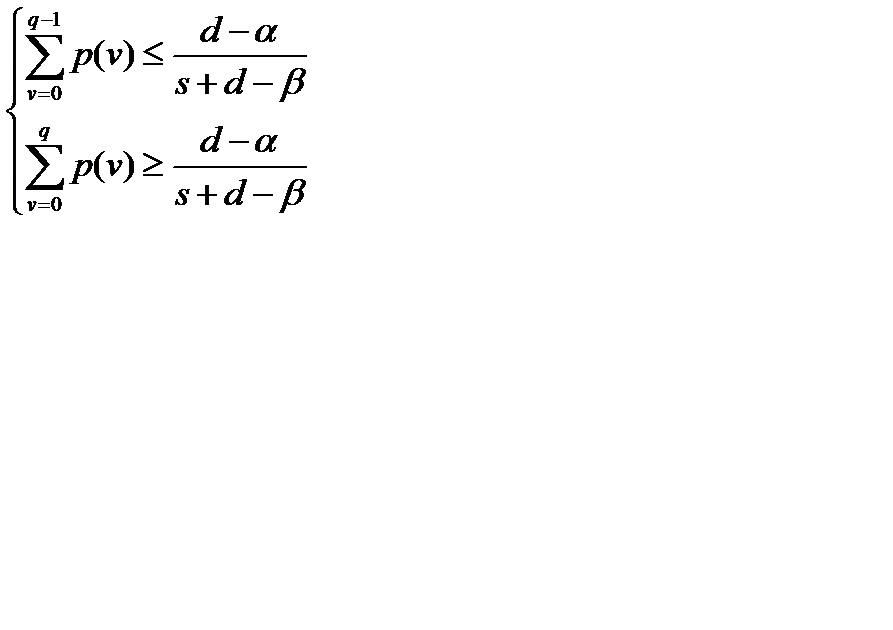 или
или 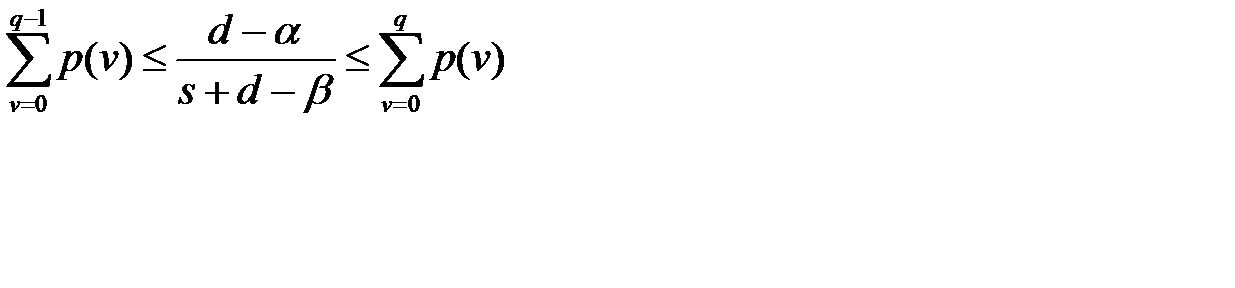 .
.
Из последней системы следует неравенство для нахождения оптимальной партии поставки
 или
или 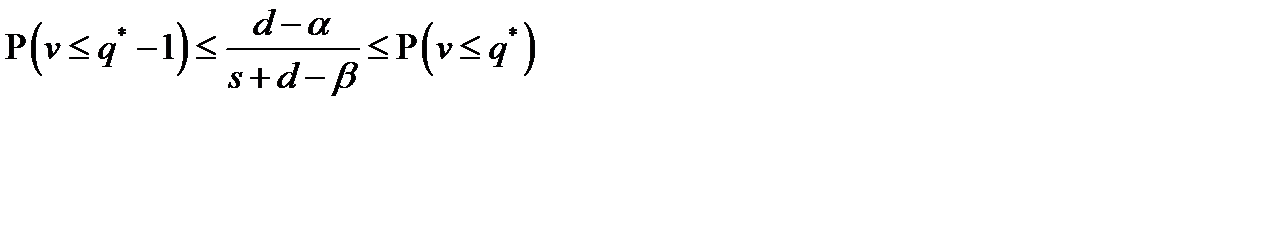 (12.17)
(12.17)
Среднее количество неиспользованной продукции равно математическому ожиданию спроса, не превышающего оптимальные значения q*:  .
.
Минимальные издержки функционирования системы в единицу времени составляют: 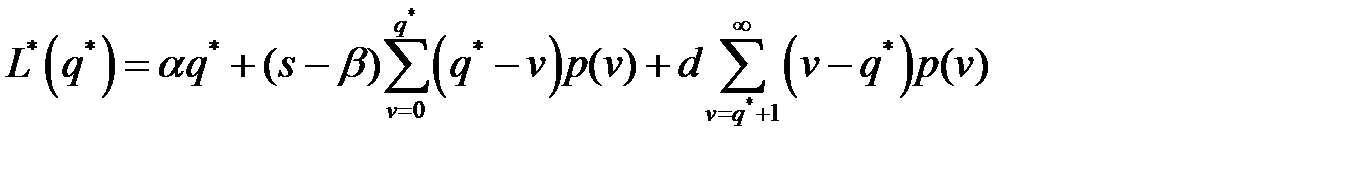 .
.
Пример 12.3. Предприятие производит продукцию, спрос на которую в течение года задан рядом распределения:
| Спрос v, тыс. шт. | ||||||
| Вероятность спроса, p(v) | 0,1 | 0,15 | 0,1 | 0,2 | 0,25 | 0,2 |
Стоимость изготовления 1000 единиц продукции равна 150 ден. ед. Издержки из-за дефицита единицы продукции составляю 0,2 ден. ед. Неиспользованная продукция в конце года реализуется по цене 50 ден. ед. за 1000. Издержки содержания составляют 10% первоначальной стоимости. Определить оптимальную партию производства продукции, среднее число неиспользованной продукции и издержки, связанные с производством, хранением и дефицитом продукции.
Решение. Спрос V на продукцию является дискретной случайной величиной. В условии задачи заданны: стоимость изготовления 1000 ед. продукции  ден. ед.; издержки дефицита одной единицы продукции d=0,2 ден. ед. , а 1000 ед. продукции –
ден. ед.; издержки дефицита одной единицы продукции d=0,2 ден. ед. , а 1000 ед. продукции –  ден. ед.; издержки содержания 1000 ед. продукции составляет
ден. ед.; издержки содержания 1000 ед. продукции составляет  ден. ед. Нереализованная продукция в конце года распродается по 50 ден. ед. Для того, чтобы найти оптимальную партию производства продукции воспользуемся неравенством (12.17), предварительно определив накопленные вероятности спроса:
ден. ед. Нереализованная продукция в конце года распродается по 50 ден. ед. Для того, чтобы найти оптимальную партию производства продукции воспользуемся неравенством (12.17), предварительно определив накопленные вероятности спроса:
| Спрос, v, тыс. шт. | ||||||
Накопленные вероятности, 
| 0,1 | 0,25 | 0,35 | 0,55 | 0,8 | 1,0 |
Вычислим величину  .
.
Следовательно, оптимальная партия производства продукции должна удовлетворять неравенству:
 .
.
Значение 0,3 находится между накопленными вероятностями 0,25 и 0,35, которым соответствуют значения спроса  = 15 и
= 15 и  = 20. Значит, оптимальное значение
= 20. Значит, оптимальное значение  тыс. ед. продукции.
тыс. ед. продукции.
Среднее количество неиспользованной продукции будет равно:
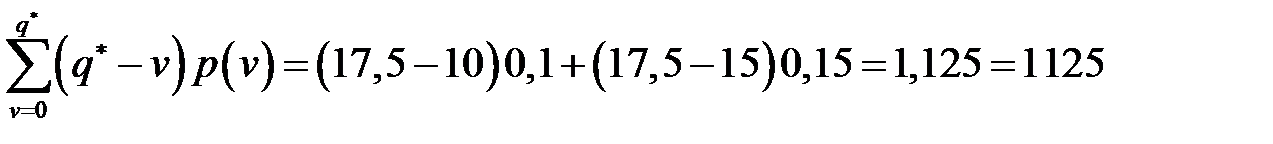 (ед. продукции).
(ед. продукции).
Минимальные издержки работы системы составят:
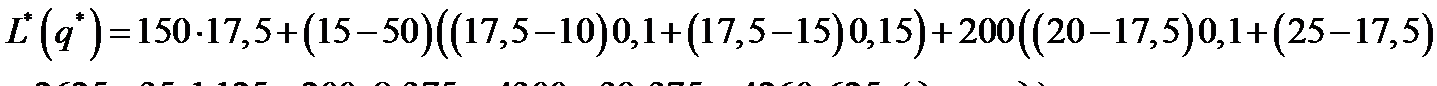
Дата добавления: 2015-09-29; просмотров: 1311;
