Лекция 13 Экономико-математические методы и модели во внешнеэкономической и в коммерческой деятельности

Вопросы, изучаемые на лекции:

13.1. Экономико-математические методы сетевого планирования и управления во внешнеэкономической и в коммерческой деятельности

13.2. Виды сетевых моделей и правила их построения во внешнеэкономической и в коммерческой деятельности

13.3. Определение продолжительности работ

Экономико-математические методы сетевого планирования и управления во внешнеэкономической и в коммерческой деятельности.

Сетевое планирование и управление построено на теории графов, основы которой, разработаны Л. Эйлером в 1736 году при решении задачи «Кенигсбергских мостов». Город Кенигсберг (Калининград) тогда был рас положен на берегах и двух островах реки Преголи (см. рисунок 13.1):

Рисунок 13.1

Острова с берегами были связаны между собой семью мостами. Вопрос заключался в том: «можно ли совершить прогулку таким образом, чтобы, выйдя из любого места города, вернуться в него, пройдя в точности один раз по каждому мосту?»

Л. Эйлер (в возрасте 20 лет) доказал невозможность построить такой маршрут. Для решения задачи Л. Эйлер обозначил каждую часть суши точкой. Поскольку связи между частями суши поддерживаются только через 7 мостов, то каждый из них изображался линией (ребром), соединяющей соответствующие части суши (вершины). В результате получалась схема, состоящая из точек А, В, С, Д (вершин) и соединяющих их линий (ребер) (рисунок 13.2).

Такие схемы называются графами. Эйлер доказал, что такого маршрута нет, а такой маршрут имеется только для графа, каждая из вершин которого связана с четным числом ребер.

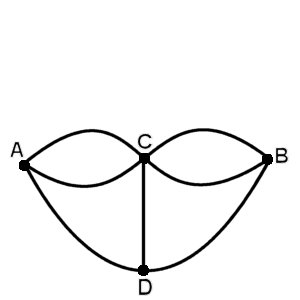
Рисунок 13.2

В 1847 году немецкий физик Кирхгоф применил теорию графов для анализа электрических цепей.

В 1878 Кэли (английский математик) сформулировал задачу «О четырех красках»: «можно ли на географической карте раскрасить страны так, чтобы никакие страны, имеющие общую границу, не были раскрашены одной краской и чтобы были использованы всего 4 краски?»

Если страны граничат по точке, то они не считаются имеющими общую границу. Такая карта показана на рисунке 13.3.

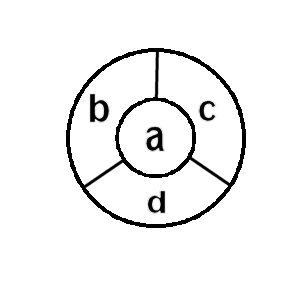
Рисунок 13.3

Только в 1976 году эту задачу удалось решить американским математикам К. Аппелю и В. Хейкену, которые доказали, что четырех красок достаточно.

В материальном производстве вершины графа - это узлы, детали, изделия, а связи между ними (вхождения деталей в узлы, узлов в изделия) можно изобразить дугами графа.

Теория графов как математическая дисциплина сформировалось к середине 30-х годов 20 века благодаря работам венгерского математика Д. Кенига.

В основу методов сетевого планирования и управления положено графическое представление комплекса работ для достижения поставленной цели в виде сетевого графика. Комплекс работ называют проектом.

Сетевой график – это совокупность G некоторого количества вершин E₁, E₂,… и установленных между ними связей , ,… , которые называются дугами или ребрами. Совокупность G (множество) вершин E и дуг называется графом и обозначается .

Отметим, что соединение вершин упорядоченно, т.е. подчиняется некоторому закону. Если определены начальные и конечные точки ребер (дуг), то такой граф называется ориентированным или орграфом. В орграфе пары вершин соединены направленными дугами (ребрами). Любые две вершины, соединенные дугой, называются смежными. Две дуги будут смежными, если они имеют хотя бы одну общую вершину. Граф полный, если каждые две различные вершины его соединены только одним ребром (дугой).

Орграф превращается в сеть, если каждой вершине поставлено в соответствие некоторое число , называемое интенсивностью вершины, а каждой дуге – неотрицательное число , называемое ее пропускной способностью. Понятие сети лежит в основе системы сетевого планирования и управления (СПУ).

Сетевой график – это, ориентированный граф без контуров, у которого начальная вершина не совпадает с конечной и дуги которого имеют одну или несколько числовых характеристик. При этом вершины орграфа отождествляются с событиями, а дуги с работами.

Работа – это любой трудовой процесс или действие, сопровождающееся затратами времени и ресурсов.

Работы на сетевых графиках обозначаются безразмерными стрелками, рядом с которыми указываются время выполнения работы, расход ресурсов, количество исполнителей и т.д. Отметим, что под работами подразумеваются не только реальные хозяйственные или технологические процессы, требующие затрат времени и ресурсов для их осуществления, но и процессы, потребляющие только время. Например, естественная сушка материалов, затвердение бетона и т.п. Считаются работами и те процессы, которые не требуют ни затрат времени, ни ресурсов. Это так называемые зависимости или фиктивные работы Они показывают, что одна работа не может совершаться раньше другой. На сетевых графиках фиктивные работы обычно изображаются пунктирными стрелками ( ).

Событие – это итог того или иного процесса, промежуточный или окончательный результат выполнения одной или нескольких предшествующих работ, который позволяет приступить к последующим. Событие не имеет протяженности во времени. Событие совершается тогда, когда закончены все предшествующие ему работы. Оно становится предпосылкой для начала следующих за ним работ. Каждое событие, включенное в сетевой график, должно быть полно, точно и всесторонне определено. Формулировка его должна включать результат выполнения непосредственно предшествующих ему работ. На сетевом графике события изображаются точками, кружками, ромбами и т.д., но чаще кружками с указанием номера или цифры события. Событие – это вершины орграфа. Событие, с которого начинается выполнение проекта, является исходным, оно не имеет предшествующих работ. Событие, которое констатирует завершение проекта, называется завершающим, оно не имеет последующих работ. Все другие события называются промежуточными.

Считается, что событие произошло, когда будет закончена самая длинная из всех входящих в него работ. Поскольку все работы взаимосвязаны и начало последующей обусловлено окончанием предыдущей, то не может быть события, наступление которого не означало бы окончания, по крайней мере, одной работы и одновременно начала другой.

Путь – это любая непрерывная логическая (технологическая) последовательность работ от исходного события до завершающего, т.е. от начала выполнения проекта до конечной цели. При построении пути выполняются следующие условия:

- ни один путь не может дважды проходить через одно и то же событие;

- любой путь может проходить по фиктивной работе;

- несколько путей могут проходить через одно и то же событие.

Длина пути определяется суммой продолжительности работ, составляющих этот путь. От исходного события до завершающего, может быть много путей. При составлении и анализе сетевого графика выявляется такой путь, суммарная продолжительность работ на котором будет максимальной. Он называется критическим и обуславливает время, необходимое для выполнения всех работ, включенных в сетевой график. Все работы, составляющие критический путь, называются критическими. Они - потенциально узкое место проекта. В сети можно определить несколько критических путей. Пути, близкие к ним называются подкритическими, остальные - ненапряженные или некритические.

Любой некритический путь имеет резерв времени, который равен резкости между длиной критического пути и некритического. Работы, не лежащие на критическом пути, обладают резервом времени, т.е. они допускают сдвиги в сроках выполнения. Наличие резервов времени у некритических работ дает возможность свободно маневрировать внутренними ресурсами и этим ускорять выполнение критических и некритических работ.