Модель при наличии страхового запаса
Предположим,что спрос  на продукцию является стационарной случайной величиной с математическим ожиданием
на продукцию является стационарной случайной величиной с математическим ожиданием  и конечной дисперсией
и конечной дисперсией  . Для бесперебойной работы предприятия, при случайных колебаниях спроса, предприятию необходим некоторый запас продукции, который называют страховым запасом и обозначают
. Для бесперебойной работы предприятия, при случайных колебаниях спроса, предприятию необходим некоторый запас продукции, который называют страховым запасом и обозначают  . Вероятность того, что спрос не превысит величины
. Вероятность того, что спрос не превысит величины  , называют коэффициентом надежности и обозначают
, называют коэффициентом надежности и обозначают  . Как правило, коэффициент надежности
. Как правило, коэффициент надежности  равен 0,9; 0,95 или 0,99. Вероятность противоположного события, состоящего в том, что спрос превысит величину
равен 0,9; 0,95 или 0,99. Вероятность противоположного события, состоящего в том, что спрос превысит величину  , называют коэффициентом риска
, называют коэффициентом риска  , т. е.
, т. е.  . Если известна плотность распределения вероятностей
. Если известна плотность распределения вероятностей  спроса
спроса  , то коэффициент надежности можно вычислить по формуле:
, то коэффициент надежности можно вычислить по формуле:
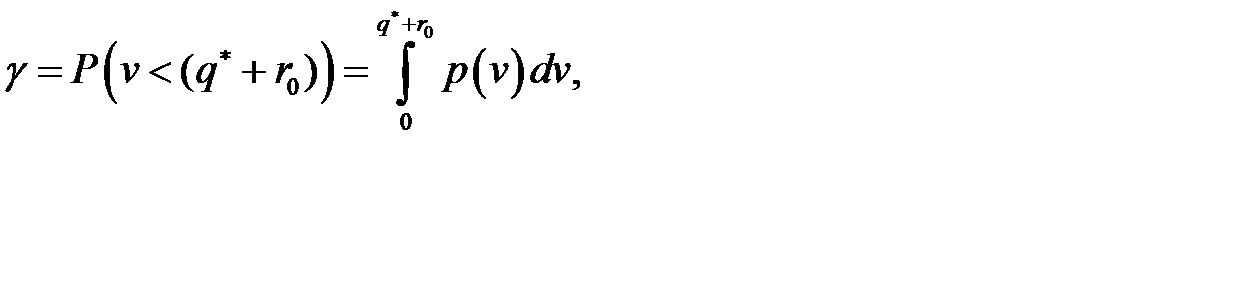
а коэффициент риска по формуле:
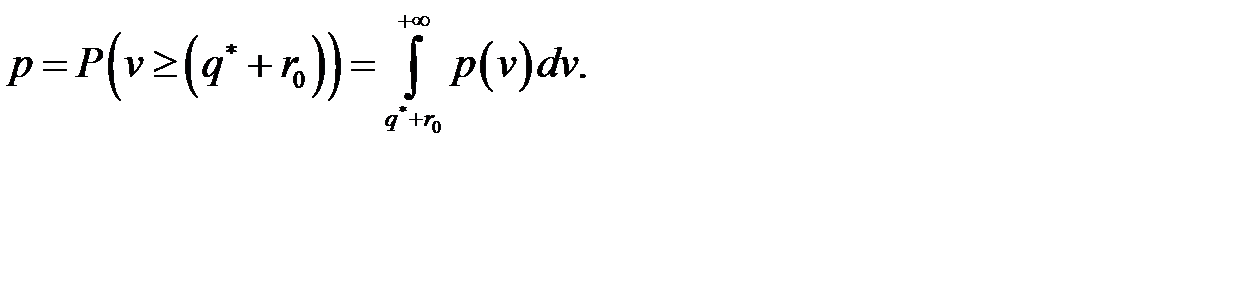
Зная закон распределения спроса и коэффициент надежности, оптимальный страховой запас можно найти из равенства:
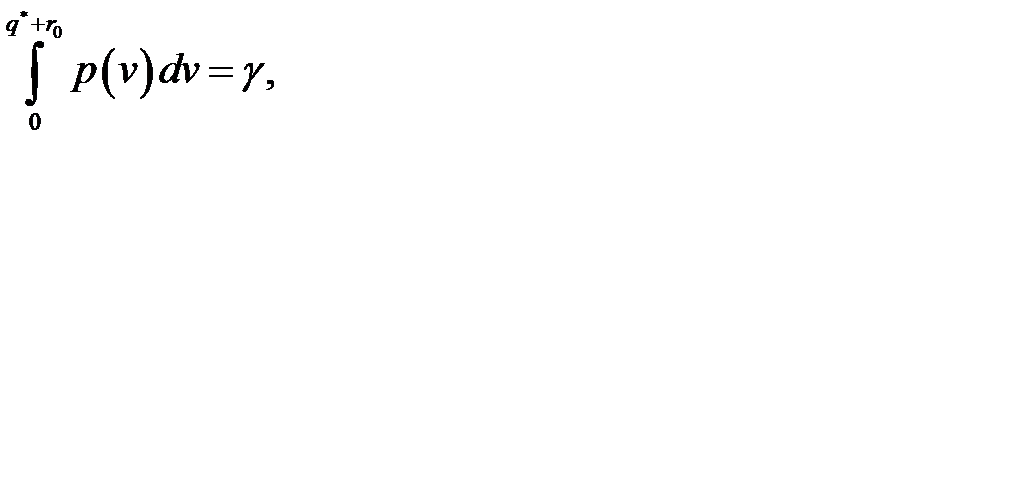 (12.18)
(12.18)
воспользовавшись соответствующей таблицей закона распределения.
При наличии страхового запаса  издержки работы системы в единицу времени описываются функцией
издержки работы системы в единицу времени описываются функцией
 ,
,
где  - средняя арифметическая спроса. Вычислив производную
- средняя арифметическая спроса. Вычислив производную  , приравняв ее нулю, находим минимальный объем партии поставки:
, приравняв ее нулю, находим минимальный объем партии поставки:  .
.
Тогда минимальные издержки составят:  .
.
Рассмотрим, как определяется страховой запас, в зависимости от закона распределения спроса.
1.Пусть спрос на продукцию подчиняется нормальному закону распределения. Функция плотности распределения вероятностей нормального закона имеет вид
 ,
,
где 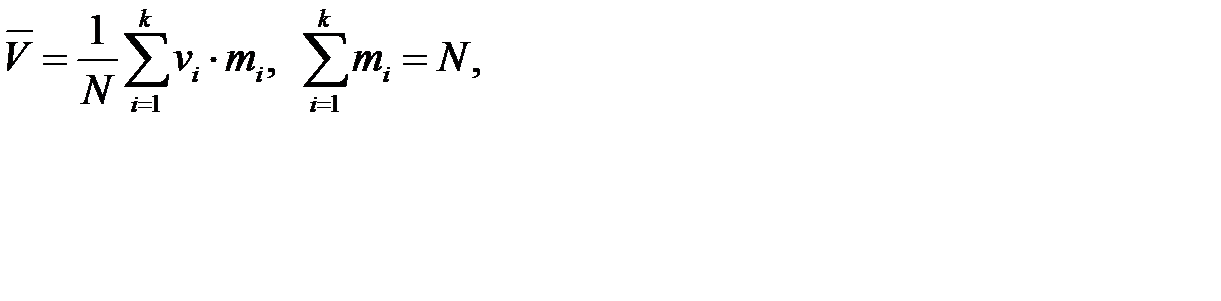 - средняя арифметическая спроса, которая является оценкой математического ожидания;
- средняя арифметическая спроса, которая является оценкой математического ожидания; 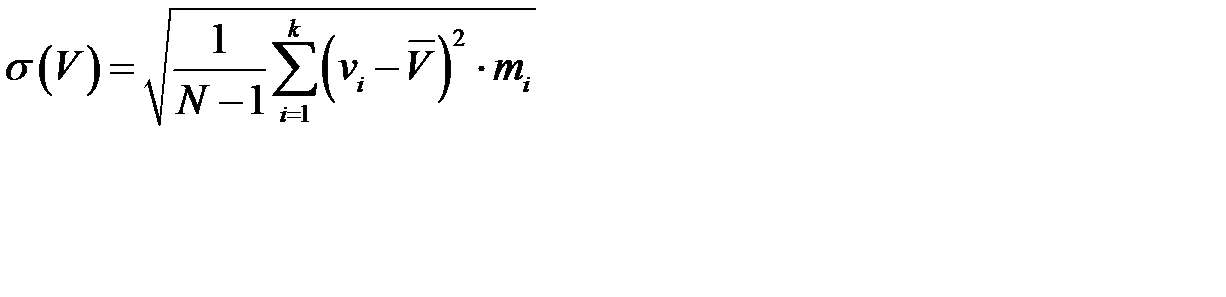 - среднее статистическое квадратическое отклонение спроса;
- среднее статистическое квадратическое отклонение спроса;  - частота, с которой встречается величина спроса
- частота, с которой встречается величина спроса  ;
; 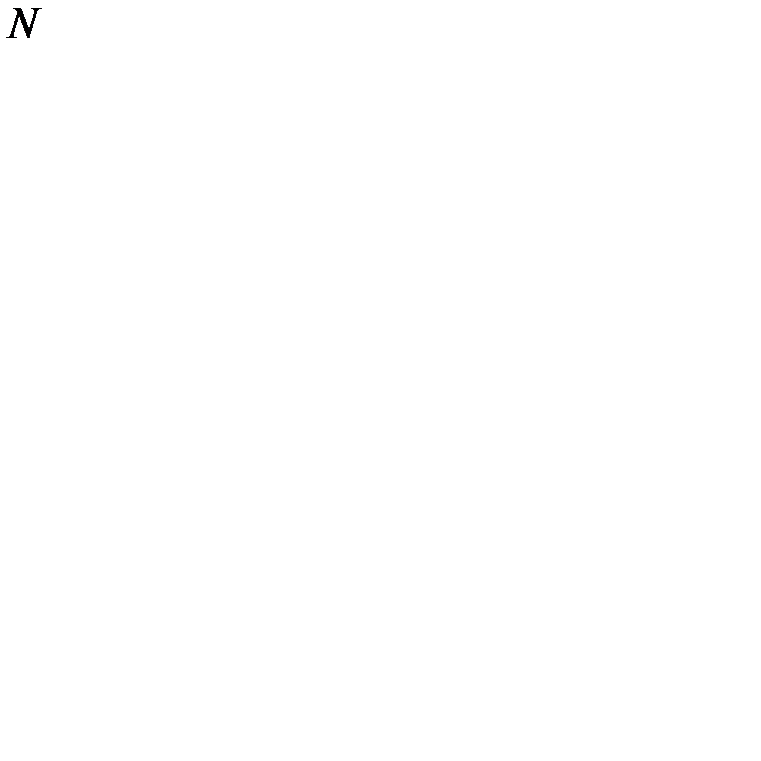 - количество наблюдений.
- количество наблюдений.
Выполнив замену  в функции
в функции  и воспользовавшись центральной предельной теоремой, преобразуем плотность нормального закона к виду
и воспользовавшись центральной предельной теоремой, преобразуем плотность нормального закона к виду  . Функция
. Функция  - это плотность распределения центрированной и нормированной случайной величины, имеющей нормальное распределение. Для того чтобы найти оптимальный страховой запас при нормальном законе распределения нужно по заданному коэффициенту риска
- это плотность распределения центрированной и нормированной случайной величины, имеющей нормальное распределение. Для того чтобы найти оптимальный страховой запас при нормальном законе распределения нужно по заданному коэффициенту риска  (или по коэффициенту надежности
(или по коэффициенту надежности  ) найти значение центрированной и нормированной случайной величины
) найти значение центрированной и нормированной случайной величины  (
(  ) из равенств
) из равенств
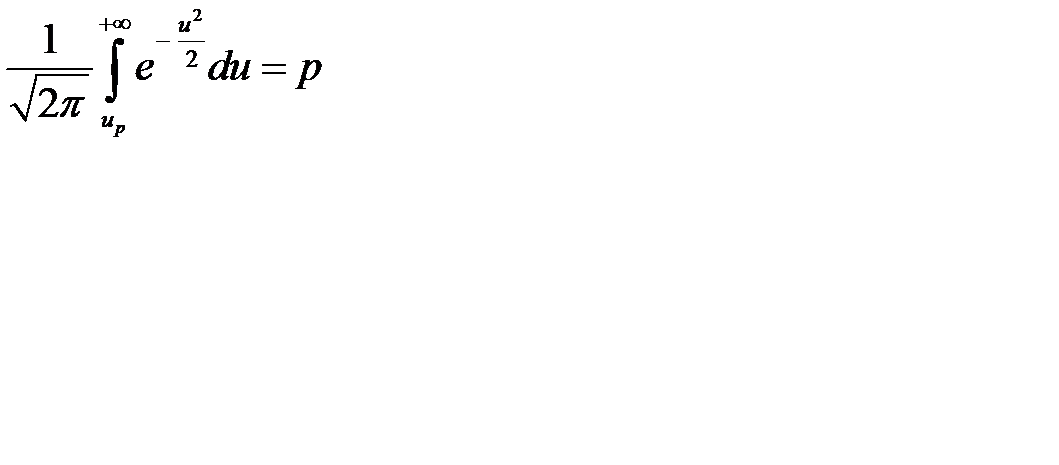 или
или 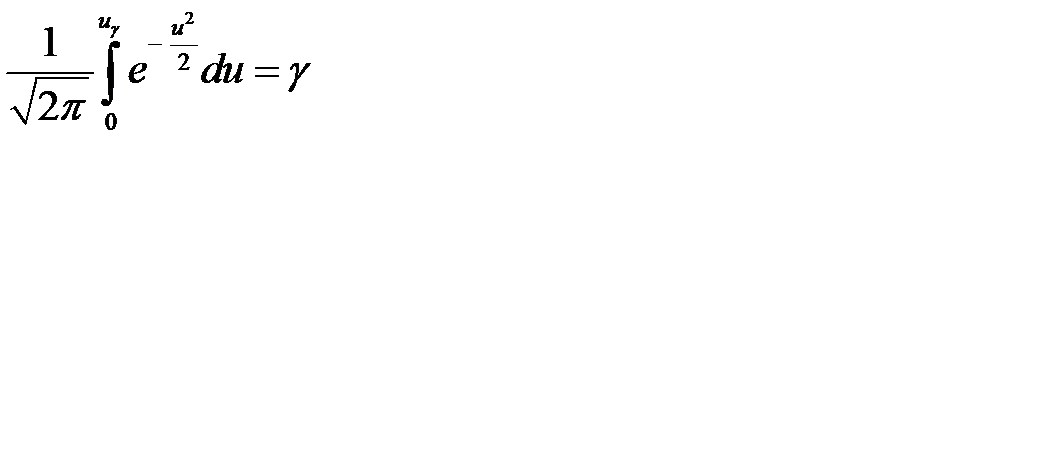 .
.
Поскольку  , то
, то 
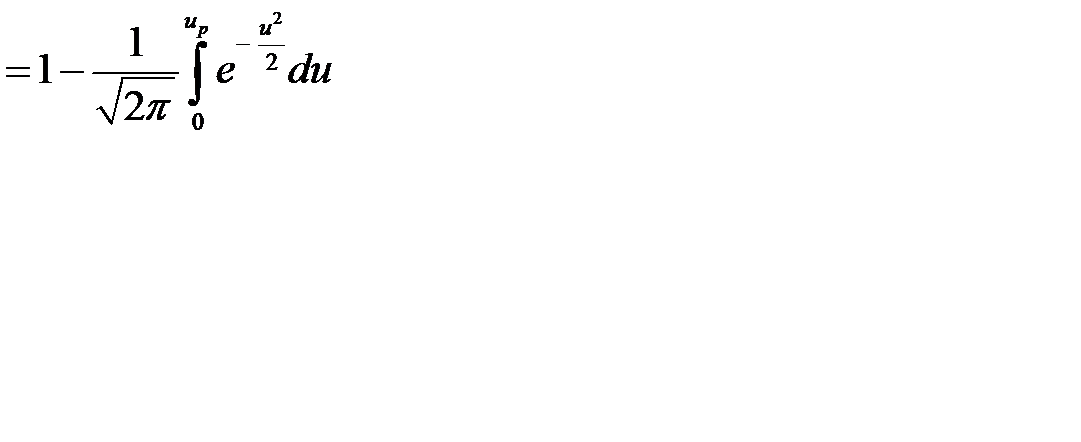 , где
, где  - функция Лапласа. Зная коэффициент риска
- функция Лапласа. Зная коэффициент риска  (или коэффициент надежности
(или коэффициент надежности  ), по таблице функции Лапласа находим
), по таблице функции Лапласа находим  . Страховой запас определяется таким образом, чтобы случайный спрос, не превосходил суммы среднего значения спроса и страхового запаса
. Страховой запас определяется таким образом, чтобы случайный спрос, не превосходил суммы среднего значения спроса и страхового запаса  с вероятностью
с вероятностью  , т. е.
, т. е.  . Учитывая, что
. Учитывая, что  , получим формулу для определения страхового запаса при нормальном законе распределения:
, получим формулу для определения страхового запаса при нормальном законе распределения: 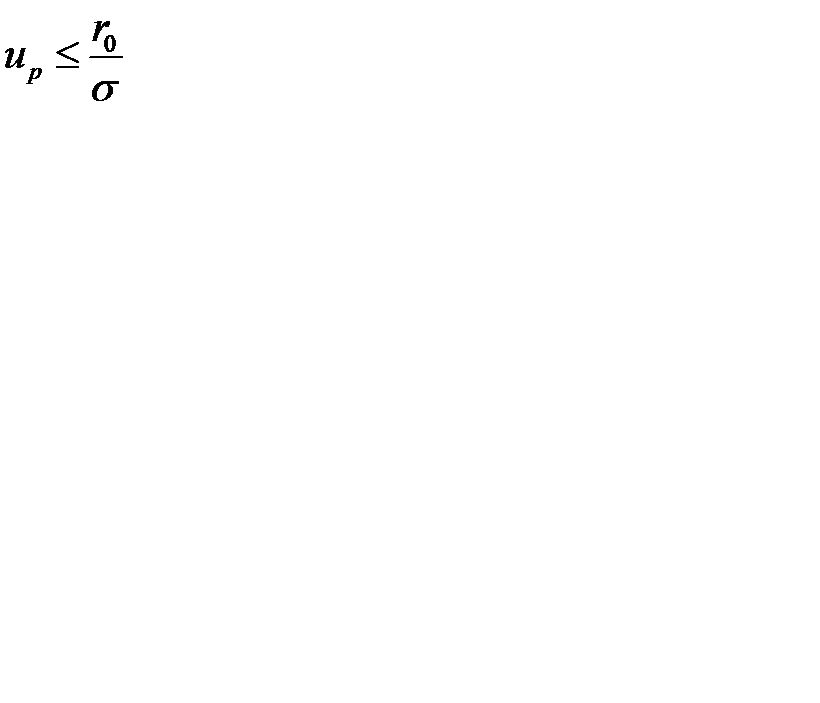
 или
или  . Из этого неравенства находим минимальное значение страхового запаса:
. Из этого неравенства находим минимальное значение страхового запаса:  . Минимальные издержки при нормальном законе распределения определяются по формуле:
. Минимальные издержки при нормальном законе распределения определяются по формуле:
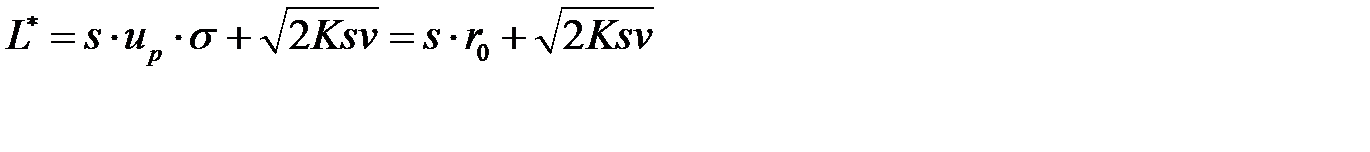 .
.
2.Пусть спрос описывается показательным законом распределения с плотностью распределения вероятностей
 .
.
Оптимальный страховой запас находим из равенства
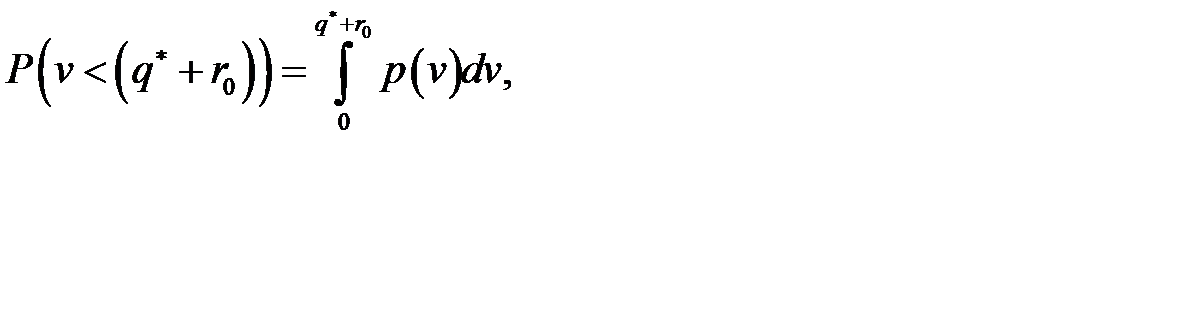 т. е.
т. е. 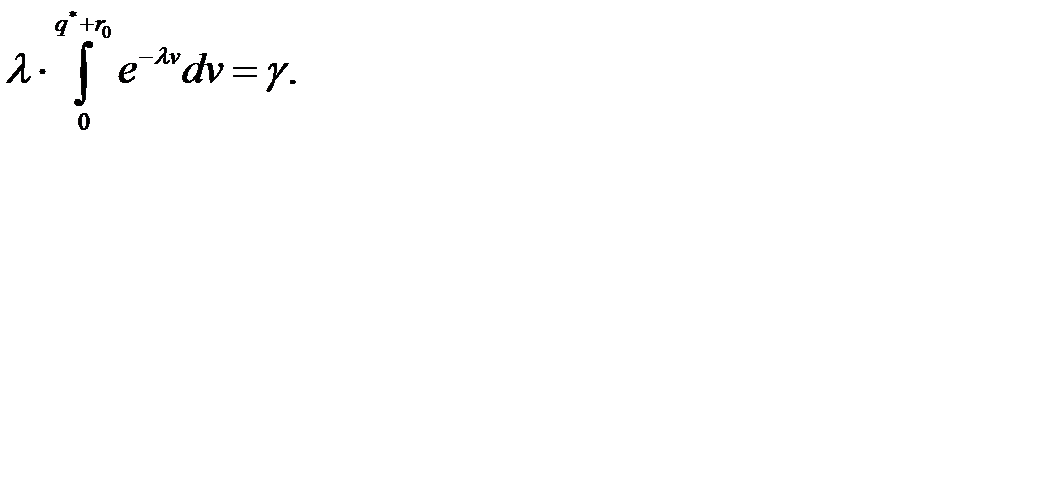
Поскольку оценка параметра 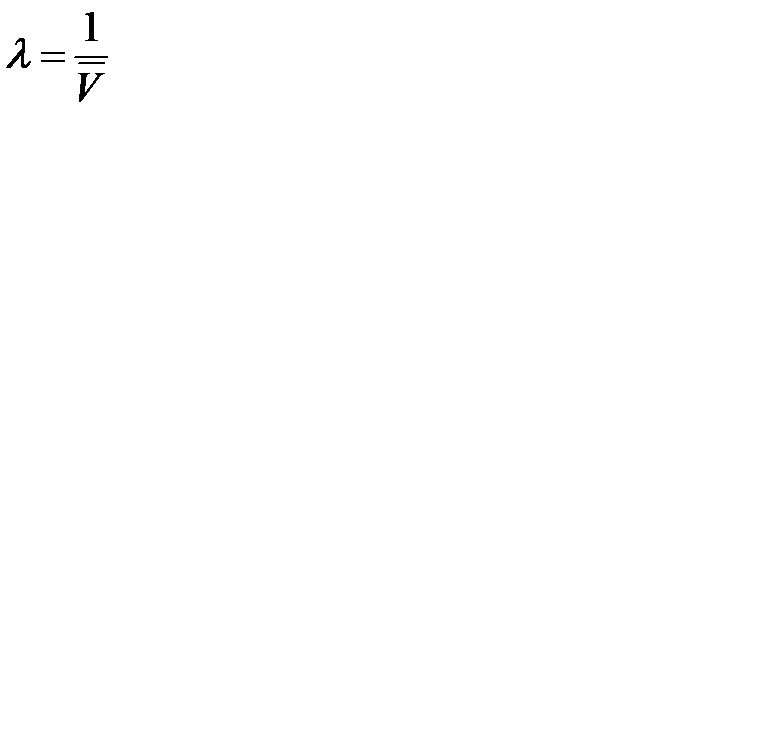 , то получим равенство
, то получим равенство 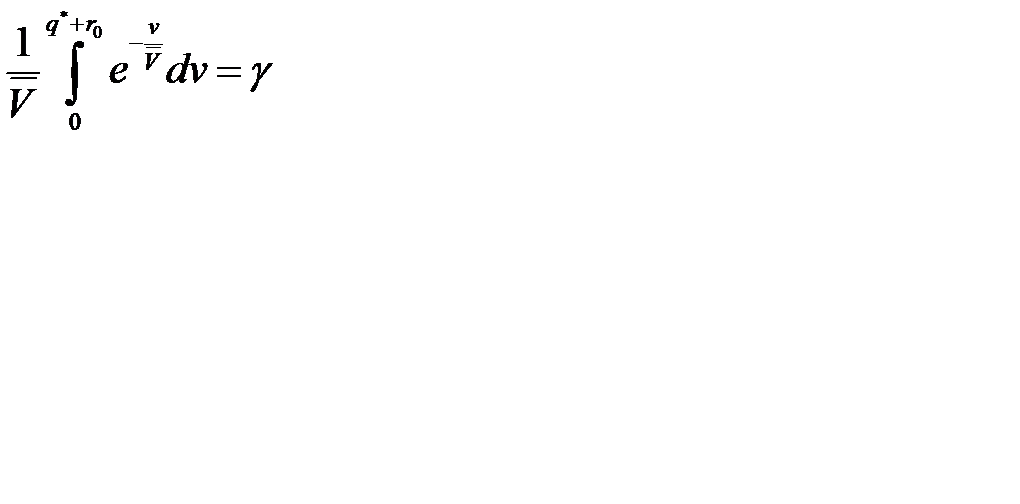 , из которого последовательно находим:
, из которого последовательно находим:
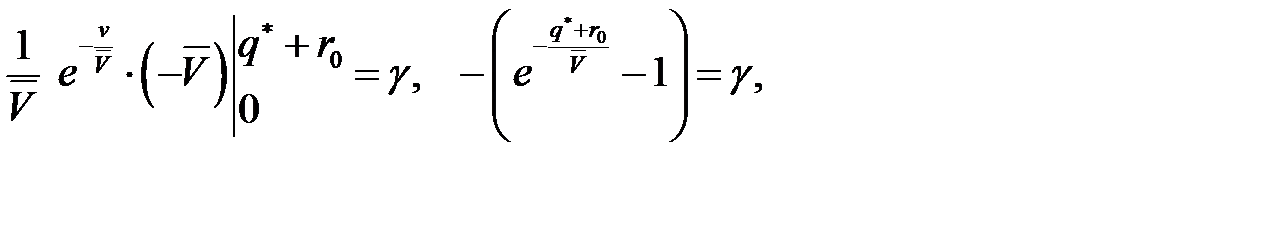


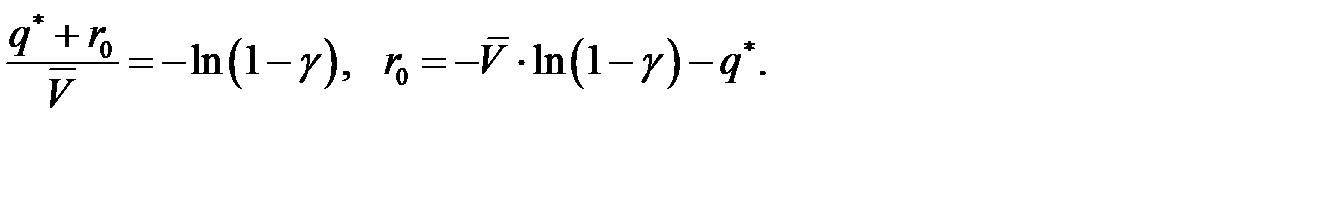
Пример 12.4.На кондитерской фабрике для упаковки готовой продукции используется упаковочная бумага. Затраты на организацию заказа составляют 50 ден.ед. Ежедневная потребность в упаковочной бумаге в течение года приведена в таблице
Потребность в
упаковочной
бумаге,  , кг , кг
| [0,100) | [100,200) | [200,300) | [300,400) | [400,500) | [500,600) | [600,700) | [700,800) | [800,900) | [900,1000) |
Частота, 
|
Определить величину страхового запаса упаковочной бумаги, гарантирующего бесперебойное снабжение с надежностью  и минимальные издержки обеспечения упаковочной бумагой в течение года при наличии страхового запаса, если стоимость хранения 1кг упаковочной бумаги составляет 10 ден. ед. в год.
и минимальные издержки обеспечения упаковочной бумагой в течение года при наличии страхового запаса, если стоимость хранения 1кг упаковочной бумаги составляет 10 ден. ед. в год.
Решение. Вначале определим закон распределения спроса на упаковочную бумагу. Для этого построим гистограмму. На оси О  отложим интервалы спроса и на каждом интервале построим прямоугольник, площадь которого равна относительной частоте спроса (рисунок 12.2).
отложим интервалы спроса и на каждом интервале построим прямоугольник, площадь которого равна относительной частоте спроса (рисунок 12.2).
По виду гистограммы можно сделать предположение о нормальном законе распределении спроса на упаковочную бумагу. Проверим гипотезу о том, что распределение спроса на упаковочную бумагу подчиняется нормальному закону распределения по следующей схеме.
0 100 200 300 400 500 600 700 800 900 1000 
|

|

Рисунок 12.2
1. Сформулируем основную гипотезу  - спрос подчиняется нормальному закону распределения и альтернативную гипотезу
- спрос подчиняется нормальному закону распределения и альтернативную гипотезу  - спрос не подчиняется нормальному закону распределения.
- спрос не подчиняется нормальному закону распределения.
2. Зададим уровень значимости  .
.
3. Объем выборки задан 
4. Для проверки гипотезы  воспользуемся критерием хи - квадрат:
воспользуемся критерием хи - квадрат:
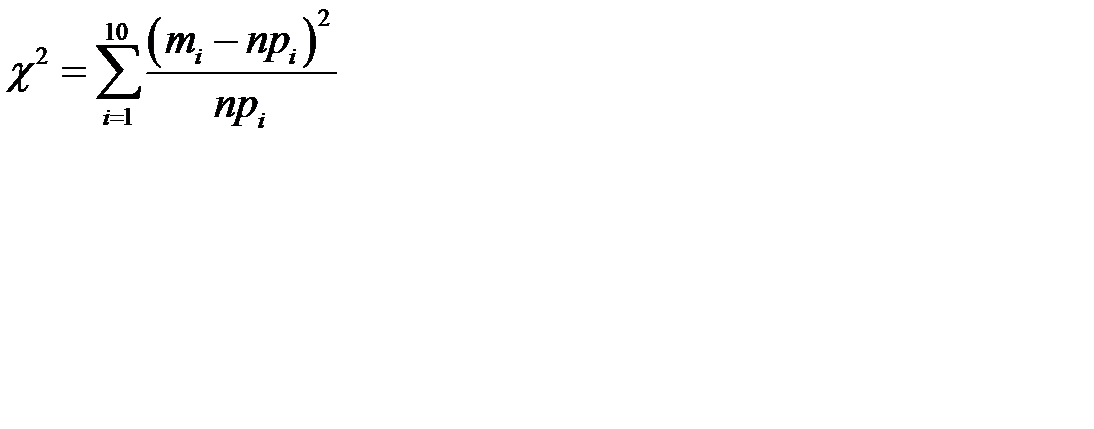 .
.
По таблице критических значений  - распределения по уровню значимости
- распределения по уровню значимости  и числу степеней свободы
и числу степеней свободы  находим квантиль
находим квантиль  . Тогда интервал
. Тогда интервал  определяет область принятия гипотезы, а полуинтервал
определяет область принятия гипотезы, а полуинтервал  - критическую область.
- критическую область.
5. Вычислим числовые характеристики выборки  и
и  , которые являются оценками математического ожидания
, которые являются оценками математического ожидания  и среднего квадратического отклонения
и среднего квадратического отклонения  нормального закона распределения. Среднее арифметическое равно:
нормального закона распределения. Среднее арифметическое равно: 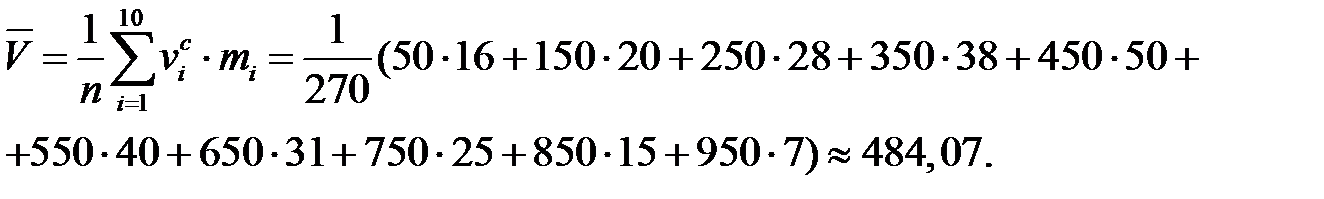
Среднее статистическое квадратическое отклонение:
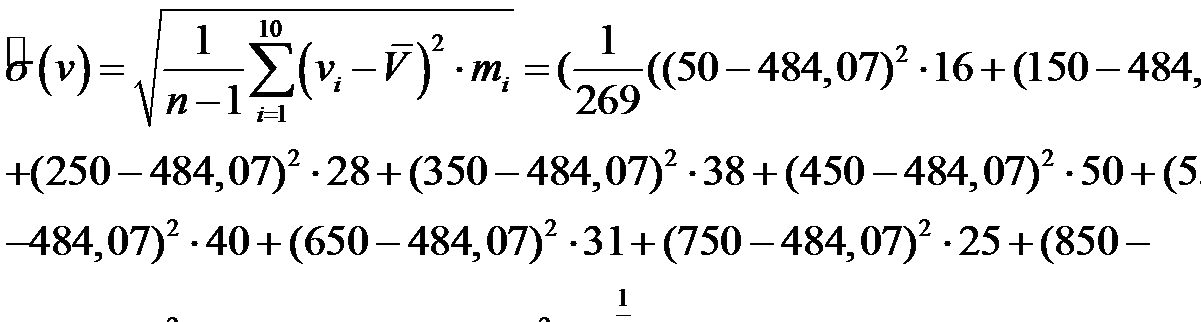
 Тогда функция нормального закона распределения будет иметь вид:
Тогда функция нормального закона распределения будет иметь вид:
 . Теоретические частоты вычислим по формуле:
. Теоретические частоты вычислим по формуле:
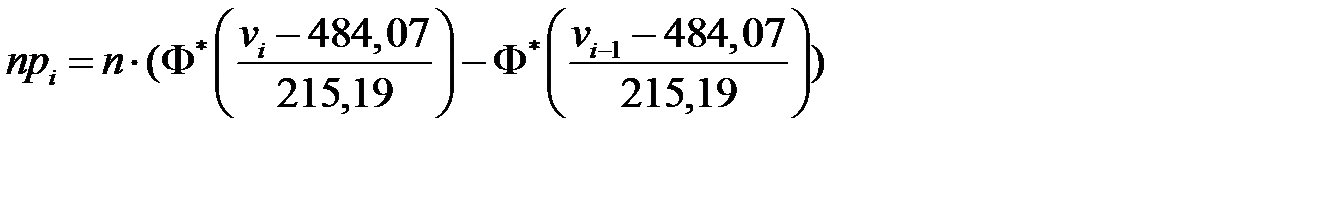 , при этом наименьшее значение дроби
, при этом наименьшее значение дроби  заменяем на «
заменяем на «  », а наибольшее – на «
», а наибольшее – на «  ».
».
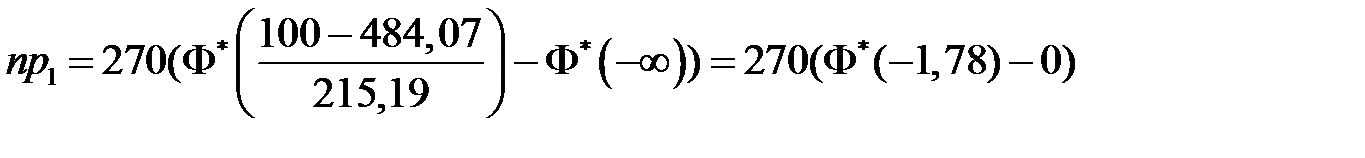 =270(0,0375-0)= =10,125; и т. д.
=270(0,0375-0)= =10,125; и т. д.
Вычисление значения  по эмпирическим данным сведем в таблицу 12.4.
по эмпирическим данным сведем в таблицу 12.4.
Таблица 12.4
Потребность
в упаковочной
бумаге,  (кг) (кг)

| Частоты,

| 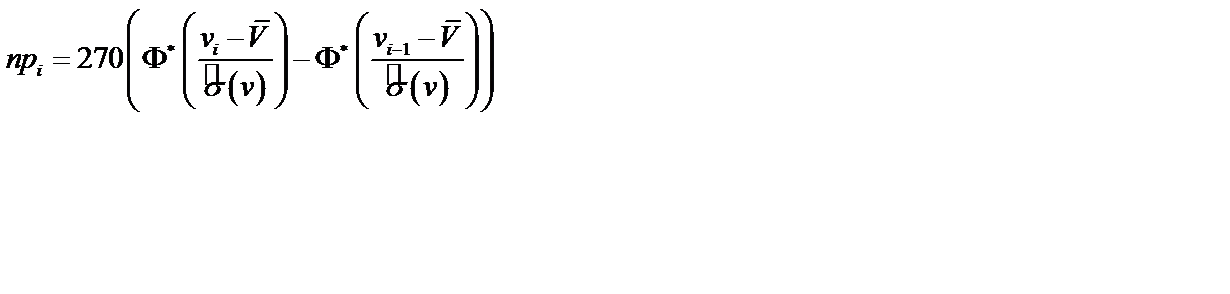
| 
| 
|
 [0;100) [0;100)
| 10,125 | 34,516 | 3,4430 | |
| [100; 200) | 15,093 | 24,0787 | 1,5952 | |
| [200; 300) | 27,405 | 0,3540 | 0,0129 | |
| [300; 400) | 41,418 | 11,6824 | 0,2821 | |
| [400; 500) | 48,492 | 2,2741 | 0,0469 | |
| [500; 600) | 47,925 | 62,8056 | 1,3105 | |
| [600; 700) | 36,693 | 32,4103 | 0,8833 | |
| [700; 800) | 23,733 | 1,6053 | 0,0676 | |
| [800; 900) | 12,042 | 8,7498 | 0,7266 | |
| [900; 1000] | 7,074 | 0,0055 | 0,0008 | |
 8,3689 8,3689
|
По таблице критических значений  - распределения по уровню значимости
- распределения по уровню значимости  и числу степеней свободы
и числу степеней свободы  находим
находим  . Так как
. Так как  8,3689 меньше
8,3689 меньше  , то оснований для отклонения нулевой гипотезы
, то оснований для отклонения нулевой гипотезы  нет.
нет.
Итак, спрос на упаковочную бумагу подчиняется нормальному закону распределения, и страховой запас определим по формуле:  , где
, где  находим по таблице значений функции
находим по таблице значений функции  . Минимальные издержки при наличии страхового запаса равны:
. Минимальные издержки при наличии страхового запаса равны:

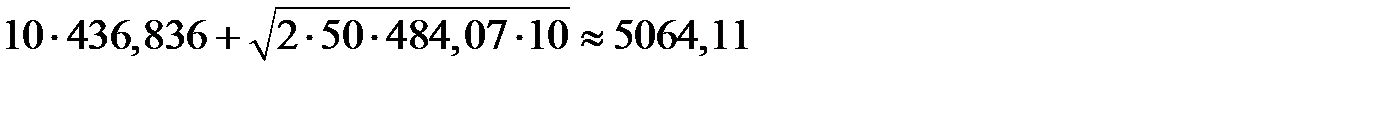 (ден.ед.)
(ден.ед.)
Дата добавления: 2015-09-29; просмотров: 902;
