Уравнения в полных дифференциалах
Уравнение вида
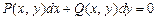 (22.33)
(22.33)
называется уравнением в полных дифференциалах, если его левая часть есть полный дифференциал некоторой функции 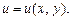 т. е.
т. е.
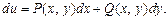 (22.34)
(22.34)
Тогда уравнение (22.33) равносильно уравнению 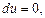 общий интеграл которого определяется формулой
общий интеграл которого определяется формулой
 (22.35)
(22.35)
где С – произвольная постоянная.
Для того чтобы дифференциальное уравнение (22.33) было уравнением в полных дифференциалах, необходимо и достаточно, чтобы выполнялось тождество
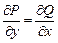 (22.36)
(22.36)
при условии, что 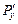 и
и 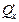 – непрерывны.
– непрерывны.
При решении уравнения (22.33) следует сделать следующее:
1) проверить выполнение равенства (22.36);
2) если равенство (22.36) выполняется, следует определить функцию  из системы уравнений
из системы уравнений
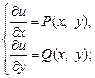 (22.37)
(22.37)
3) общий интеграл уравнения (22.33) получают в виде (22.35).
Пример 1. Решить дифференциальное уравнение:
1) 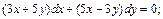 2)
2) 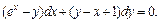
Решение. 1) Это уравнение вида (22.33), где 
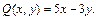 Проверим выполнение условия (22.36):
Проверим выполнение условия (22.36):
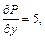
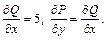
Значит, заданное уравнение – в полных дифференциалах. Определим функцию u(x, y) из системы уравнений (22.37)
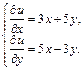 (22.38)
(22.38)
Интегрируем первое уравнение по x, считая y постоянной величиной:
 (22.39)
(22.39)
где в качестве произвольной постоянной относительно переменной x выступает функция 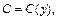 которую нужно найти. Для этого функцию (22.39) дифференцируем по y:
которую нужно найти. Для этого функцию (22.39) дифференцируем по y:
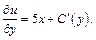
Правую часть полученного равенства приравниваем к правой части второго уравнения системы (22.38):
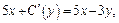
откуда получаем 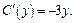
Интегрируем последнее равенство:
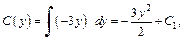
где 
Подставляем найденную функцию C(y) в (22.39):

Согласно формуле (22.35), получаем:
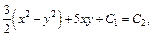
где  т. е.
т. е.
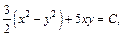
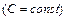 – общий интеграл заданного дифференциального уравнения.
– общий интеграл заданного дифференциального уравнения.
2) В заданном примере имеем 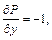
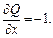 Значит, это уравнение в полных дифференциалах. Найдем функцию u(x, y) из системы уравнений
Значит, это уравнение в полных дифференциалах. Найдем функцию u(x, y) из системы уравнений
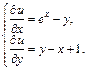 (22.40)
(22.40)
Интегрируем первое уравнение системы:
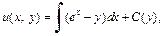 т. е.
т. е.
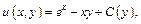 где C(y) – функция от y, которую надо найти. Дифференцируем последнее равенство по y:
где C(y) – функция от y, которую надо найти. Дифференцируем последнее равенство по y:
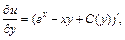

Используя полученное равенство и второе равенство системы (22.40), приравниваем их правые части:
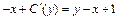 или
или 
Интегрированием получаем далее
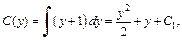
где 
Тогда 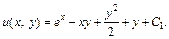
Общий интеграл заданного дифференциального уравнения:
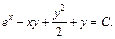
Пример 2. Решить задачу Коши:
1) 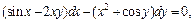

2) 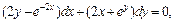
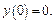
Решение. 1) В заданном примере 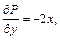
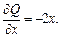 Значит, это уравнение в полных дифференциалах. Найдем функцию u(x, y) из системы уравнений
Значит, это уравнение в полных дифференциалах. Найдем функцию u(x, y) из системы уравнений
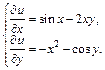 (22.41)
(22.41)
Интегрируем первое уравнение системы:
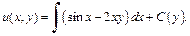
Получаем:
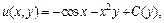
где C(y) – функция от y, которую надо найти. Дифференцируем последнее равенство по y:
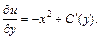
Используем полученное равенство и второе равенство системы (22.41), приравниваем их правые части:
 или
или 
Интегрированием получаем:
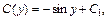
где 
Тогда общий интеграл заданного дифференциального уравнения имеет вид:
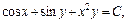
где 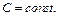
Используем начальное условие 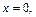
 и находим константу C:
и находим константу C:
 или
или 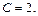
Поэтому решением задачи Коши является
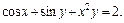
2) Проверяем условие (22.36): 
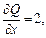 значит, заданное дифференциальное уравнение является уравнением в полных дифференциалах. Находим функцию u(x, y) из системы уравнений
значит, заданное дифференциальное уравнение является уравнением в полных дифференциалах. Находим функцию u(x, y) из системы уравнений
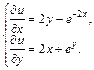 (22.42)
(22.42)
Интегрируем первое уравнение системы:
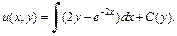
Получаем:
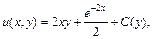
где C(y) – неизвестная функция от y, которую надо найти. Дифференцируем последнее равенство по y:

Используя полученное равенство и второе равенство системы (22.42), приравниваем правые части:
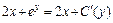 или
или 
Интегрированием получаем:
 где
где 
Тогда общий интеграл заданного дифференциального уравнения имеет вид:
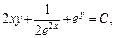 где
где 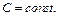
Используя начальное условие 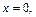
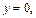 находим константу С:
находим константу С:
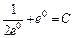 или
или 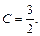
Тогда решением задачи Коши является:
 или
или 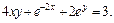
Дата добавления: 2015-09-29; просмотров: 811;
