Уравнения высших порядков
Линейным однородным дифференциальным уравнением n-го порядка называется уравнение
(22.55)
Общим решением этого уравнения является функция
где 
– линейно-независимые частные решения уравнения (22.55), 
– произвольные постоянные.
Совокупность n линейно-независимых на (a, b) решений уравнения (22.55) называется фундаментальной системой решений.
Частным случаем уравнения (22.55) является линейное однородное уравнение n-го порядка с постоянными коэффициентами:
(22.56)
где 
– действительные числа.
Для нахождения частных решений уравнения (22.56) составляют характеристическое уравнение
(22.57)
путем замены в уравнении (22.56) производных определенного порядка на соответствующие степени параметра 
на 
где 
Каждому корню уравнения (22.57) соответствует определенное частное решение дифференциального уравнения. Вид частного решения зависит от типа корня уравнения (22.57). Возможны следующие четыре случая, которые определяет правило частных решений:
1. Если 
– действительный корень кратности 1 (простой корень), то ему соответствует решение вида 
2. Если 
– действительный корень кратности k, то ему соответствует k частных решений:
3. Если 
– пара комплексно-сопряженных корней, то им соответствует два частных решения:
4. Если 
– пара k-кратных комплексно-сопряженных корней, то им соответствуют 2k частных решения:
Поскольку характеристическое уравнение (22.57) имеет n корней, считая их кратность, то для дифференциального уравнения (22.56) по правилу частных решений можно указать n решений 
Эти решения образуют фундаментальную систему решений.
Тогда общее решение уравнения (22.56) определяется формулой
где 
– произвольные постоянные.
Пример 1. Найти общее решение уравнения:
1) 
2) 
3) 
4) 
Решение. 1) Составим характеристическое уравнение
Решая его, получаем: 
– два действительных простых корня. Им соответствуют частные решения 
Общее решение заданного дифференциального уравнения имеет вид:
где 
– произвольные постоянные.
2) Составим характеристическое уравнение
Решая его, получаем: 
– два действительных простых корня. Им соответствуют частные решения 
Общее решение заданного дифференциального уравнения имеет вид:
где – произвольные постоянные.
3) Характеристическое уравнение имеет вид:
или 
Отсюда 
– корень кратности 2.
Тогда решения 
и 
образуют фундаментальную систему решений исходного дифференциального уравнения, а общее решение имеет вид:
где – произвольные постоянные.
4) Характеристическое уравнение заданного дифференциального уравнения
Его корни: 
– простые комплексно-сопряженные. Тогда этой паре корней характеристического уравнения соответствуют два линейно-независимых частных решения заданного дифференциального уравнения:
Получаем общее решение исходного дифференциального уравнения:
где – произвольные постоянные.
Пример 2. Найти общее решение дифференциального уравнения:
1) 
2) 
3) 
4) 
Решение. 1) Запишем характеристическое уравнение заданного дифференциального уравнения
Его корнями будут 
т. е. корни характеристического уравнения действительные и различные. Им соответствуют три линейно-независимых частных решения:
Общее решение заданного дифференциального уравнения имеет вид: 
где 
– произвольные постоянные.
2) Составим характеристи ческое уравнение заданного дифференциального уравнения
Его корни: 
Им соответствуют три линейно-независимых частных решения:
Общее решение имеет вид:
где 
– произвольные постоянные.
3) Характеристическое уравнение имеет вид:
Его корни: 
(корень кратности 2), 
Им соответствуют четыре линейно-независимых частных решения вида
Общее решение имеет вид:
где 
– произвольные постоянные.
4) Запишем характеристическое уравнение заданного дифференциального уравнения
Преобразуем это уравнение к виду
Отсюда, очевидно, что корни характеристического уравнения 
– комплексно-сопряженные кратности 3. Тогда им соответствуют шесть линейно-независимых частных решений вида
Общее решение заданного дифференциального уравнения имеет вид:
где 
– произвольные постоянные.
Пример 3. Решить задачу Коши:
1) 
2) 
Решение. 1) Характеристическое уравнение имеет вид:
или 
Его корень 
– корень кратности 2. Тогда решения 
образуют фундаментальную систему решений. Общее решение имеет вид:
Чтобы найти константы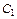 
и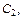 
дифференцируем найденное общее решение:
Затем подставляем начальные условия в выражения для y и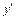 
и решаем систему уравнений относительно 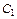и 
Получаем 
Тогда решение задачи Коши:
2) Характеристическое уравнение
или 
Его корни: 
– корень кратности 3, 
Им соответствуют пять линейно-независимых решений:
Общее решение заданного дифференциального уравнения имеет вид:
Для определения констант 
продифференцируем полученное общее решение последовательно четыре раза:
Подставляя в выражения для 
начальные условия, находим константы:
Тогда решение задачи Коши:
Дата добавления: 2015-09-29; просмотров: 649;