линейных однородных уравнений

1. Любому простому действительному корню характеристического уравнения (22.81) соответствует решение

где коэффициенты определяют из системы (22.80) при найденном т. е.

(22.82)

Тогда общее решение системы (22.78) записывают в виде

где – произвольные постоянные.

2. Каждому комплексному корню и ему сопряженному соответствуют два линейно-независимых действительных решения. Для построения этих решений находим комплексное решение по формуле (22.79) для корня как и в случае 1, и выделяем действительную и мнимую части этого решения (корень уже не рассматриваем, так как новых решений системы (22.78) он не дает).

3. Если – корень кратности k, то решение, соответствующее этому корню, ищут в виде

(22.83)

где – многочлен с неопределенными коэффициентами степени

Чтобы найти коэффициенты многочленов подставляем решение (22.83) в систему (22.78) и приравниваем коэффициенты подобных членов в левой и правой частях уравнений. Выразив все коэффициенты через любые k, полагаем по очереди один из них равным единице, а остальные равными нулю.

Пример 1. Решить систему однородных дифференциальных уравнений с постоянными коэффициентами:

1) 2)

Решение. 1) Характеристическое уравнение системы имеет вид:

Вычисляя определитель, получаем откуда – простые действительные корни. Частные решения системы ищем в виде

При система (22.82) имеет вид:

Эта система имеет бесконечное множество решений. Для определенности положим тогда Получаем частные решения:

При система (22.82) принимает вид:

Положим тогда

Значит, корню соответствуют частные решения:

Общее решение исходной системы запишется в виде

2) Характеристическое уравнение системы

которое приобретает вид или Уравнение имеет двукратный корень Ему соответствует решение вида

Продифференцируем функции x(t) и y(t) и подставим в исходную систему:

Сокращаем на и группируем. Получаем систему для коэффициентов

Так как кратность корня равна двум (k = 2), то выразим все коэффициенты последней системы через любые два, например, через A и B:

Полагая находим 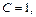Полагая находим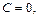

Получаем два линейно-независимых частных решения:

и

Общее решение исходной системы имеет вид:

Пример 2. Найти частное решение системы

Решение. Характеристическое уравнение системы

т. е.

Оно имеет корни Для корня составляем систему (22.82):

Полагаем тогда

Частное комплексное решение системы:

Выделяем в полученных функциях действительные (Re) и мнимые (Im) части.

Поскольку то

тогда

Сопряженный корень новых линейно-независимых решений не дает, поэтому не рассматривается. Таким образом, общее решение исходной системы:

Найдем частное решение для заданных начальных условий. Получаем:

откуда находим

Искомое частное решение системы: