Типы уравнений, допускающие понижение порядка
Уравнение вида
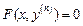 (22.46)
(22.46)
или разрешенное относительно n-йпроизводной
 (22.47)
(22.47)
решается последовательным интегрированием n раз.
Уравнение вида
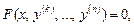 (22.48)
(22.48)
не содержащее явно искомой функции y и первых ( 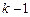 )-х ее производных,
)-х ее производных,  решают с помощью замены
решают с помощью замены 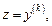 где
где 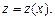 Таким образом, порядок исходного уравнения (22.48) понижается на k единиц.
Таким образом, порядок исходного уравнения (22.48) понижается на k единиц.
Приходят к уравнению
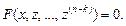
Полученное уравнение решают далее в зависимости от его типа.
Уравнение вида
 (22.49)
(22.49)
не содержащее явно независимой переменной x, решают с помощью замены
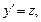 где
где 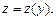

Этой заменой порядок исходного уравнения понижается на единицу, поскольку 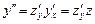 (функцию z(y) дифференцировали по x как сложную). Аналогично выражают
(функцию z(y) дифференцировали по x как сложную). Аналогично выражают 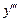 и т. д.
и т. д.
Уравнение вида
 (22.50)
(22.50)
называется однородным относительно искомой функции y и ее производных 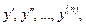 если функция F однородна относительно
если функция F однородна относительно  т. е.
т. е.
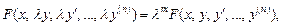
где m – степень однородности, 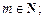
 – произвольное число.
– произвольное число.
Для решения используется замена  где
где  понижающая порядок исходного уравнения на единицу.
понижающая порядок исходного уравнения на единицу.
Пример 1. Найти общее решение уравнения:
1) 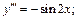 2)
2) 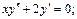
3) 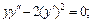 4)
4) 
Решение. 1) Заданное уравнение имеет 3-й порядок. Это дифференциальное уравнение типа (22.47). Проинтегрируем последовательно три раза:
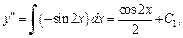
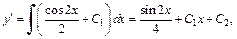

 – произвольные постоянные. Полученная функция
– произвольные постоянные. Полученная функция  и есть общее решение исходного уравнения.
и есть общее решение исходного уравнения.
2) Это уравнение 2-го порядка, не содержащее явно искомой функции y, т. е. типа (22.48). Делаем замену 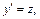 где
где 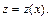 Дифференцируем замену еще раз, получаем
Дифференцируем замену еще раз, получаем  Подставляем выражения
Подставляем выражения 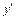 и
и  в исходное уравнение:
в исходное уравнение:
 (22.51)
(22.51)
Получили уравнение с разделяющимися переменными:


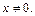
В результате интегрирования имеем:  откуда
откуда 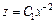 – общее решение уравнения (22.51).
– общее решение уравнения (22.51).
Возвращаемся к старым переменным:
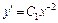 – уравнение первого порядка. Интегрируем его:
– уравнение первого порядка. Интегрируем его:
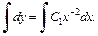
Получаем  – общее решение исходного уравнения.
– общее решение исходного уравнения.
3) Это уравнение 2-го порядка, не содержащее явно независимой переменной x, т. е. типа (22.49). Делаем замену 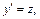 где
где 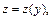
 Дифференцируем замену по x как сложную функцию, получаем:
Дифференцируем замену по x как сложную функцию, получаем: 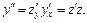 Подставляем выражения для
Подставляем выражения для 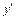 и
и  в исходное уравнение:
в исходное уравнение:
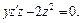 (22.52)
(22.52)
Уравнение (22.52) – это уравнение с разделяющимися переменными. Решаем его:
 или
или 

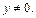
Далее интегрируя, имеем:
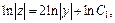 откуда
откуда
 – общее решение уравнения (22.52).
– общее решение уравнения (22.52).
Возвращаемся к старым переменным, получаем  – уравнение с разделяющимися переменными. Тогда
– уравнение с разделяющимися переменными. Тогда
 или
или 
Интегрируем:
 или
или 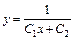 – общее решение исходного дифференциального уравнения.
– общее решение исходного дифференциального уравнения.
4) Это уравнение 2-го порядка, однородное относительно  и
и  так как
так как
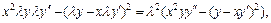
где  – произвольное число.
– произвольное число.
Это уравнение типа (22.50). Делаем замену  где
где 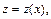 отсюда получаем:
отсюда получаем:
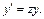 (22.53)
(22.53)
Дифференцируем это равенство еще раз:

С учетом (22.53) получаем:
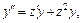

Подставляем выражения для 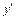 и
и  в исходное уравнение:
в исходное уравнение:

Делим его на 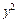

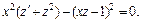
После упрощения имеем уравнение
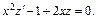
Делим его почленно на 

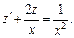 (22.54)
(22.54)
Получили линейное уравнение 1-го порядка. Решаем его, например, методом Бернулли:

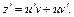
Тогда (22.54) примет вид:
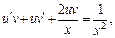 т. е.
т. е. 
Полагаем 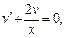 откуда
откуда 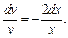
Интегрирование приводит к равенству

Тогда имеем:
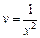 – искомая функция v.
– искомая функция v.
Далее имеем:
 т. е.
т. е. 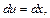 что означает
что означает 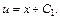
Отсюда 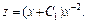
Возвращаемся к старым переменным:
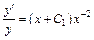 или
или 
Интегрируем:
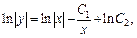 используя свойства логарифма, получаем:
используя свойства логарифма, получаем:
 или
или 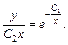
Таким образом, 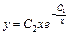 – общее решение исходного уравнения.
– общее решение исходного уравнения.
Пример 2. Найти частное решение уравнения:
1) 
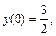

2) 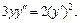
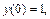
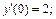
3) 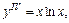


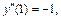

Решение. 1) Заданное уравнение имеет 2-й порядок. Делаем замену 
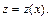 Тогда
Тогда  и заданное уравнение принимает вид:
и заданное уравнение принимает вид:
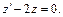
Получили дифференциальное уравнение 1-го порядка с разделяющимися переменными. Решаем его:
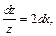
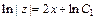 или
или 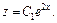
Возвращаясь к старой переменной, получим: 
Определим константу 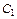 из начального условия
из начального условия 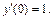 Тогда
Тогда 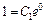 или
или  Таким образом,
Таким образом, 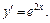 Интегрируем и получаем:
Интегрируем и получаем:

Определяем 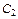 из 2-го начального условия:
из 2-го начального условия:  т. е.
т. е. 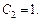
Частным решением исходного дифференциального уравнения является функция 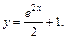
2) Это уравнение 2-го порядка, не содержащее явно переменную x. Делаем замену 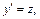
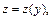
 Тогда
Тогда  и заданное уравнение примет вид
и заданное уравнение примет вид 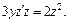 Получили уравнение 1-го порядка с разделяющимися переменными. Интегрируем его:
Получили уравнение 1-го порядка с разделяющимися переменными. Интегрируем его:
 имеем:
имеем:
 или
или 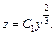
Возвращаемся к старой переменной:
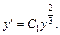
Определяем 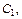 используя 2-е начальное условие:
используя 2-е начальное условие:
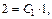 отсюда
отсюда 
Получаем  – уравнение 1-го порядка с разделяющимися переменными. Его решение:
– уравнение 1-го порядка с разделяющимися переменными. Его решение:
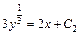 или
или 
Определяем константу 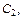 используя первое начальное условие:
используя первое начальное условие:
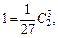 откуда
откуда 
Тогда частным решением заданного уравнения является функция 
3) Это дифференциальное уравнение 4-го порядка типа (22.47). Проинтегрируем его последовательно четыре раза:
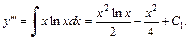
Определим константу 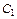 из начального условия
из начального условия  Тогда
Тогда 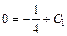 или
или 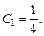
Интегрируем еще раз:
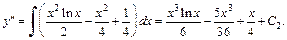
Определяем 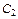 из начального условия
из начального условия 
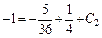 или
или 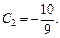
Интегрируем далее:

Из начального условия  находим
находим 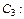
 или
или 
Интегрируем в 4-й раз:
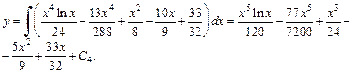
Находим константу  из начального условия
из начального условия 
 или
или 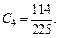
Тогда частным решением заданного дифференциального уравнения является функция
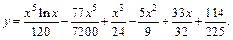
Дата добавления: 2015-09-29; просмотров: 774;
