Несобственный интеграл первого рода

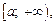
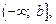
Несобственный интеграл первого рода – это обобщение интеграла на случай бесконечных промежутков числовой оси: на полупрямые 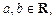и на прямую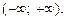

Полагаем, что для любого числа 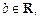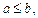существует определенный интеграл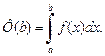

Результат нахождения предела функции Ф(b) при 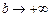назовем несобственным интегралом первого рода:

(21.1)

Несобственный интеграл первого рода называется сходящимся, если предел (21.1) существует. Если предел (21.1) не существует, то несобственный интеграл называется расходящимся. При этом за ним закрепляется значение 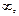если функция Ф(b) бесконечно большая на бесконечности, и не задается никакого значения, если предел функции Ф(b) при 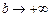не определен.

Если для функции f (x), 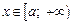можно найти первообразную F(x) на каждом конечном отрезке то справедлива формула Ньютона-Лейбница

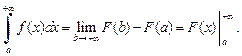(21.2)

Аналогично определяется понятие несобственного интеграла первого рода на промежутках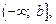

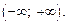
Равенство

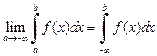(21.3)

(при условии, что предел существует) определяет сходящийся несобственный интеграл на промежутке 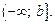Соответственно, расходящийся интеграл – если предел в левой части равенства (21.3) не существует. Если F(x) – первообразная f(x) на каждом конечном отрезке [a; b], то для данного случая справедлива формула Ньютона-Лейбница

Несобственный интеграл на промежутке рассматривают как сумму несобственных интегралов на лучах 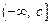и 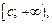где c – произвольная фиксированная точка на числовой оси:

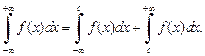(21.4)

Первый интеграл в правой части равенства (21.4) определяют в смысле формулы (21.3), а второй – в смысле формулы (21.1).

Несобственный интеграл 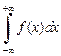называется сходящимся, если сходятся оба интеграла в правой части равенства (21.4), и расходящимся, если хотя бы один интеграл в правой части равенства (21.4) расходящийся.

Несобственный интеграл от функции f (x) на промежутке можно задать также равенством

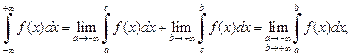
где величины a и b стремятся к бесконечности независимо друг от друга. Для вычисления несобственного интеграла на промежутке используют формулу Ньютона-Лейбница

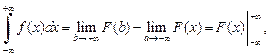
где F(x) – первообразная функция f (x).

Несобственный интеграл 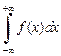сходится в смыслеглавного значения, если существует конечный предел 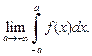Этот предел называется главным значениемнесобственного интеграла от функции f(x) в смысле Коши и обозначается:

V.p. 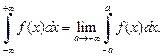(21.5)

З а м е ч а н и е 1. Для интеграла 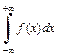следует различать сходимость, определяемую равенством (21.4), от сходимости в смысле главного значения (см. далее решение примера 4, с. 144–145).