Свойства несобственных интегралов

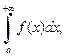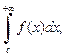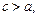1. Если сходится интеграл то сходится и интеграл где и наоборот. При этом выполняется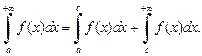

2. Если интеграл 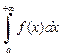сходится, то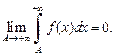

3. Свойство линейности: если сходятся интегралы 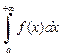и 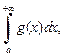то при произвольных постоянных 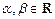сходится также интеграл 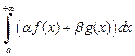и справедлива формула

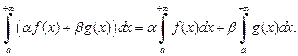
4. Если для любого 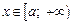справедливо неравенство 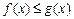и интегралы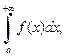 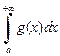сходятся, то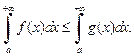

5. Если функции u(x) и v(x) имеют непрерывные производные на промежутке 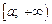и существует то из сходимости одного из интегралов 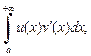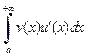вытекает сходимость другого интеграла и справедлива формула интегрирования по частям:

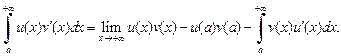(21.6)

6. Пусть выполняются следующие условия:

1) функция f (x) непрерывна на промежутке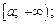

2) на промежутке определена строго монотонная функция множеством значений которой является полупрямая 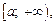и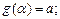

3) функция g(t) имеет непрерывную производную на промежутке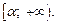

Тогда из сходимости одного из интегралов 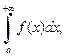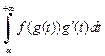вытекает сходимость другого интеграла, и справедлива формула замены переменной

(21.7)