Несобственный интеграл второго рода

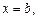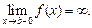Пусть функция f (x) является непрерывной на промежутке [a; b) и неограниченной в окрестности точки т. е. Тогда точка b называется особой точкойи говорят, что функция f (x) имеет особенность в точке b. Для любого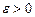 функция f (x) интегрируема на отрезке 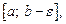т. е. существует интеграл

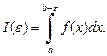(21.10)

Результат вычисления предела функци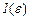и при называется несобственным интегралом второго рода:

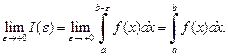(21.11)

Несобственный интеграл второго рода (21.11) называется сходящимся, если предел (21.11) существует. Если функция 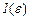является бесконечно большой, то несобственный интеграл считают равным бесконечности. Если предел (21.11) не существует, то интеграл не принимает никакого значения. В последних двух случаях несобственный интеграл второго рода называется расходящимся.

Если для функции f (x), определенной на полуинтервале [a, b), известна ее первообразная F(x), то для вычисления интеграла (21.11) используется формула Ньютона-Лейбница

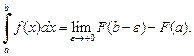(21.12)