Второго рода от неотрицательных функций
1. Признак сравнения
Пусть функции f (x) и g(x) определены на промежутке [a; b) и для них выполняется неравенство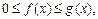 
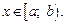Тогда из сходимости интеграла 
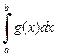следует сходимость интеграла 
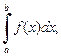а из расходимости интеграла 
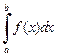вытекает расходимость интеграла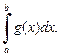 
2. Предельный признак сравнения
Пусть на промежутке [a; b) определены положительные функции f (x) и g(x), для которых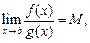 
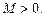Тогда оба интеграла 
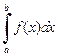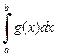и вместе сходятся или оба вместе расходятся.
3. Пусть неотрицательная функция f (x) определена на промежутке [a; b) и для x, близких к b, удовлетворяет условию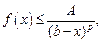 
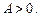Тогда при 
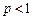несобственный интеграл 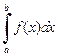сходится. Если для x, близких к b, выполняется неравенство 
, 
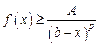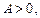тогда при 
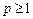интеграл от этой функции на промежутке [a; b) расходится.
Дата добавления: 2015-09-29; просмотров: 687;