Второго рода

Если функция f (x) непрерывна на промежутке [a, b), функция 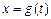определена на полуинтервале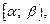 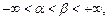и имеет на нем непрерывную производную, причем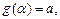 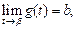то справедлива формула 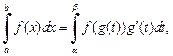при этом интегралы в ней оба сходятся или оба расходятся.

Аналогично определяется несобственный интеграл второго рода, если 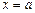– особая точка функции f (x):

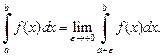(21.13)

Если особая точка 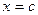функции f (x) является внутренней точкой отрезка [a; b] (функция f (x) имеет в этой точке разрыв второго рода), то несобственный интеграл второго рода функции f (x) по отрезку [a; b] определяется равенством:

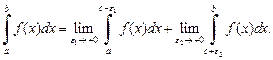(21.14)

З а м е ч а н и е 1. Следует различать сходимость, определенную равенством (21.14), и сходимость в смысле главного значения (21.15), которая определяется следующим образом: пусть функция f (x) определена на отрезке [a; b] с особой точкой 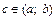и интегрируема на любом отрезке, принадлежащем полуинтервалам [a; c) и (c; b]. Если для 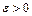такого, что 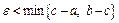существует

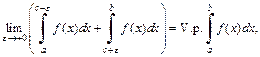(21.15)

то он называется главным значением несобственного интеграла второго рода, а функция f (x) – интегрируемой по Коши.

Всюду далее будем рассматривать сходимость, определенную равенством (21.14).