Вычисление поверхностного интеграла второго рода
 Произведение
Произведение 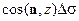 есть проекция площадки
есть проекция площадки 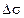 на плоскость Оху (см. рис.); аналогичное утверждение справедливо и для произведений
на плоскость Оху (см. рис.); аналогичное утверждение справедливо и для произведений 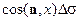 и
и 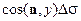 :
:
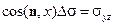 ,
, 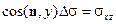 ,
, 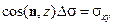
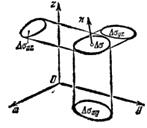
Пусть поверхность Ф такова, что всякая прямая, параллельная оси Oz пересекает ее в одной точке. Тогда уравнение поверхности можно написать в виде z = z(x, y). Обозначая через D проекцию поверхности Ф на плоскость Оху, получим
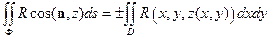
При этом перед двойным интегралом берется знак плюс, если 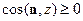 , и знак минус, если
, и знак минус, если 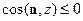 .
.
Аналогично вычисляются интегралы
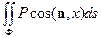 ,
, 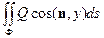
Второй способ (по разработке Павельева_Поверхн_Интегралы_кр_Версия.pdf).
Поверхностный интеграл второго рода от непрерывного во всех точках поверхности векторного поля G(x, y, z) = P(x, y, z)i+ Q(x, y, z)j+ R(x, y, z)k по ориентированной поверхности Ф (поток векторного поля Gчерез поверхность Ф) будем вычислять по формуле:
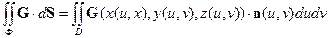 (3)
(3)
где n(u, v) − главная нормаль к поверхности Ф, соответствующая заданной стороне поверхности.
Если поверхность задана явно, например, уравнением z = z(x, y), 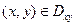 , то будем считать, что поверхность задана параметрическими уравнениями (с параметрами х, у): x = x,у = у, z = z(x, y),
, то будем считать, что поверхность задана параметрическими уравнениями (с параметрами х, у): x = x,у = у, z = z(x, y), 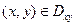 . При этом главная нормаль равна
. При этом главная нормаль равна 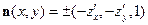 , скалярное произведение равно
, скалярное произведение равно 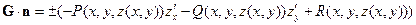
Для вычисления поверхностного интеграла второго рода воспользуемся формулой (полученной с использованием (3))
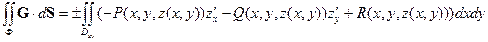
Дата добавления: 2015-10-13; просмотров: 937;
