Формула интегрирования по частям для несобственного
Интеграла второго рода
Если функции u(x) и v(x) имеют непрерывные производные на промежутке [a, b), а также существует 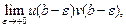 то из сходимости одного из интегралов
то из сходимости одного из интегралов 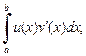
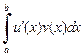 вытекает сходимость другого, и справедлива формула
вытекает сходимость другого, и справедлива формула
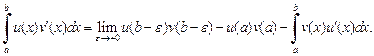
Формула замены переменной в несобственном интеграле
Дата добавления: 2015-09-29; просмотров: 777;
