От знакопеременных функций
Если 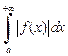 сходится, то несобственный интеграл
сходится, то несобственный интеграл 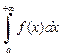 называется абсолютно сходящимся.
называется абсолютно сходящимся.
1. Если несобственный интеграл первого рода сходится абсолютно, то он сходится.
2. Если интеграл 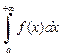 абсолютно сходящийся, а функция g(x) ограничена на промежутке
абсолютно сходящийся, а функция g(x) ограничена на промежутке 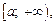 то интеграл
то интеграл 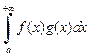 также сходится абсолютно.
также сходится абсолютно.
З а м е ч а н и е 1. Если несобственный интеграл первого рода от знакопеременной функции не сходится абсолютно, то это еще не означает, что он расходится. Для исследования на сходимость данного интеграла необходимо использовать другие признаки, в частности, признак Абеля-Дирихле: пусть функции f (x) и g(x) определены и непрерывны на промежутке 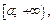 причем функция g(x) монотонно стремится к нулю при
причем функция g(x) монотонно стремится к нулю при 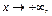 имеет непрерывную производную
имеет непрерывную производную 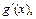 а функция f(x) имеет ограниченную первообразную F(x) при
а функция f(x) имеет ограниченную первообразную F(x) при 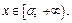 Тогда интеграл
Тогда интеграл 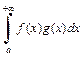 сходится.
сходится.
З а м е ч а н и е 2. Всюду далее будем исследовать интегралы на сходимость в смысле определений (21.1), (21.3) и (21.4). В смысле главного значения необходимо исследовать только те примеры, в которых это требуется по условию.
Пример 1. Исследовать на сходимость интегралы:
1) 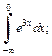 2)
2) 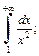 3)
3) 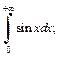 4)
4) 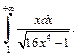
В случае сходимости вычислить их.
Решение. 1) По определению (21.3) несобственного интеграла имеем:
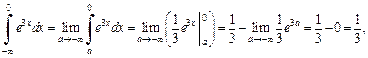
значит, интеграл сходится.
2) По определению (21.1) несобственного интеграла имеем:
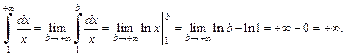
Интеграл расходится, так как первообразная 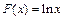 является бесконечно большой функцией на бесконечности.
является бесконечно большой функцией на бесконечности.
3) Интеграл 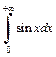 расходится, так как функция
расходится, так как функция
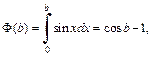
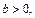
не стремится ни к какому пределу при 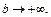
4) Вычисляем:
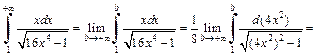
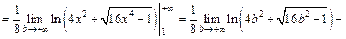
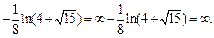
Интеграл расходится.
Пример 2. Исследовать, при каких значениях p сходится несобственный интеграл 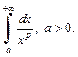
Решение. По определению (21.1) имеем:
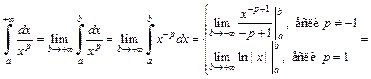
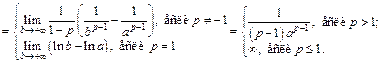
Следовательно, интеграл 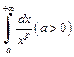 сходится, если
сходится, если 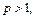 и расходится, если
и расходится, если 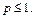
Пример 3. Вычислить несобственный интеграл первого рода:
1) 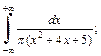 2)
2) 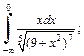 3)
3) 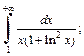
4) 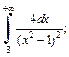 5)
5) 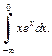
Решение. 1) Выделим в знаменателе подынтегрального выражения полный квадрат и представим заданный интеграл в виде суммы двух интегралов:

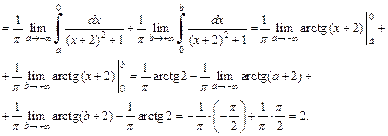
2) Используем метод поднесения под знак дифференциала. Для этого, выделив производную квадратного трехчлена в числителе, получим:
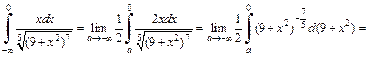
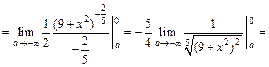
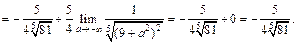
3) Вычисляем:
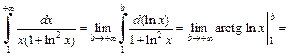
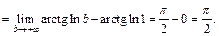
4) Представим подынтегральную функцию в виде суммы простейших дробей:
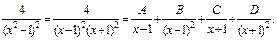
Далее приводим дроби к общему знаменателю и приравниваем числители:
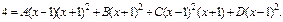 (21.8)
(21.8)
Неизвестные коэффициенты найдем с помощью метода частных значений:
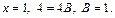
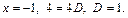
Вычислим производную от обеих частей равенства (21.8):
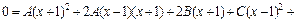
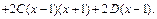
Тогда для 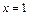 получаем:
получаем: 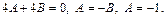
Для 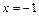 имеем:
имеем: 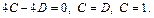
В итоге получаем:
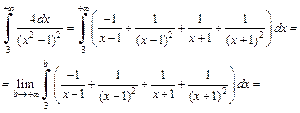
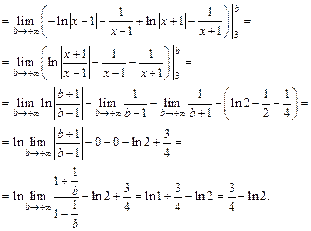
5) Применим формулу интегрирования по частям:
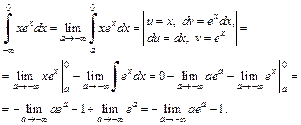
Для вычисления предела используем правило Лопиталя (по переменной a):
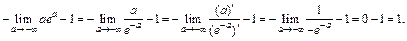
Пример 4. Найти главное значение несобственного интеграла:
1) 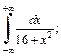 2)
2) 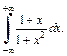
Решение. 1) Найдем главное значение данного интеграла по определению (21.5):
V.p. 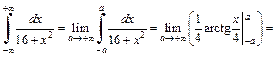
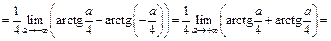
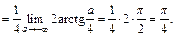
Заметим, что вычисление интеграла по формуле (21.4) также дает 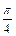 (просьба убедиться самостоятельно), т. е. он сходится и в обычном смысле.
(просьба убедиться самостоятельно), т. е. он сходится и в обычном смысле.
2) Найдем главное значение данного интеграла по определению (21.5):
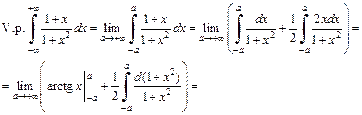
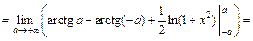
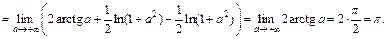 Можно убедиться, что интеграл
Можно убедиться, что интеграл 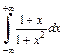 является расходящимся в обычном смысле.
является расходящимся в обычном смысле.
Пример 5. Исследовать интеграл на сходимость, используя признак сравнения:
1) 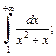 2)
2) 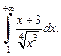
Решение. 1) При 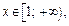 функция
функция 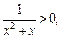 причем
причем 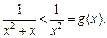 Интеграл
Интеграл 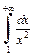 сходится, так как
сходится, так как
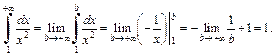
Поэтому, согласно признаку сравнения, интеграл 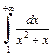 сходится.
сходится.
2) Функция 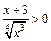 при
при 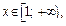 причем
причем 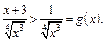 Интеграл
Интеграл 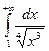 расходится, так как
расходится, так как
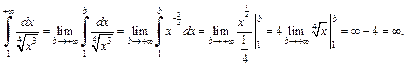
Поэтому, согласно признаку сравнения, интеграл 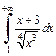 расходится.
расходится.
Пример 6. Исследовать на сходимость несобственные интегралы по предельному признаку сравнения:
1) 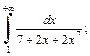 2)
2) 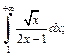 3)
3) 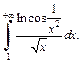
Решение. 1) Функция 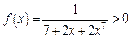 при
при 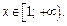 Рассмотрим функцию
Рассмотрим функцию 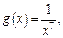 интеграл от которой сходится (пример 2, с. 141 данного пособия).
интеграл от которой сходится (пример 2, с. 141 данного пособия).
Найдем 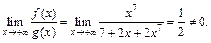 Поэтому, согласно предельному признаку сравнения заключаем, что
Поэтому, согласно предельному признаку сравнения заключаем, что 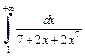 также сходится.
также сходится.
2) Функция 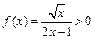 при
при 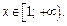 Рассмотрим функцию
Рассмотрим функцию 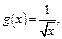 интеграл от которой расходится (пример 2, с. 141).
интеграл от которой расходится (пример 2, с. 141).
Находим:
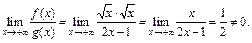 Поэтому, согласно предельному признаку сравнения,
Поэтому, согласно предельному признаку сравнения, 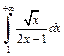 расходится.
расходится.
3) Функция 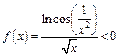 при
при 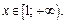 Поэтому исследуем на сходимость интеграл
Поэтому исследуем на сходимость интеграл 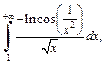 который будет сходиться или расходиться одновременно с заданным интегралом. Используем эквивалентность бесконечно малых функций:
который будет сходиться или расходиться одновременно с заданным интегралом. Используем эквивалентность бесконечно малых функций: 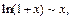
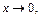
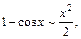
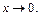 Сделаем следующие преобразования:
Сделаем следующие преобразования: 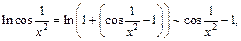
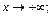
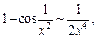
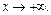 Поэтому имеем
Поэтому имеем 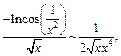
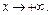 Так как известно, что несобственный интеграл от функции
Так как известно, что несобственный интеграл от функции 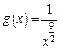 сходится на промежутке
сходится на промежутке 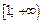 (пример 2, с. 141 данного пособия), то сходится также интеграл
(пример 2, с. 141 данного пособия), то сходится также интеграл 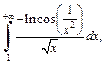 а вместе с ним и заданный интеграл
а вместе с ним и заданный интеграл 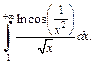
Пример 7. Исследовать на сходимость интеграл 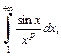 где
где 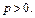
Решение. Используем признак Абеля-Дирихле. Функция 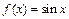 имеет ограниченную первообразную
имеет ограниченную первообразную 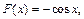
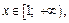 функция
функция 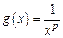 монотонно убывает и имеет непрерывную производную. Кроме того,
монотонно убывает и имеет непрерывную производную. Кроме того, 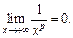 Таким образом, все условия признака Абеля-Дирихле выполняются, а значит интеграл
Таким образом, все условия признака Абеля-Дирихле выполняются, а значит интеграл 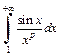 сходится.
сходится.
Пример 8. Исследовать интеграл на абсолютную сходимость:
1) 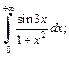 2)
2) 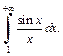
Решение. 1) Так как 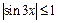 для любого
для любого 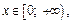 то
то 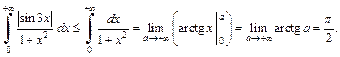
Следовательно, интеграл 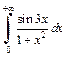 сходится абсолютно.
сходится абсолютно.
2) Интеграл 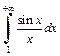 сходится в силу признака Абеля-Дирихле (см. пример 7, с. 147). Рассмотрим интеграл
сходится в силу признака Абеля-Дирихле (см. пример 7, с. 147). Рассмотрим интеграл 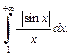 Так как
Так как 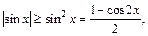 то для любого
то для любого 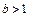 имеем:
имеем:
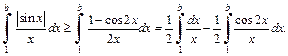 (21.9)
(21.9)
Осуществив предельный переход в неравенстве (21.9) при 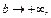 получаем:
получаем:
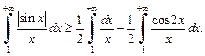
Интеграл 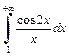 сходится в силу признака Абеля-Дирихле, а интеграл
сходится в силу признака Абеля-Дирихле, а интеграл 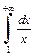 расходится (пример 2, с. 141 данного пособия). Приходим к выводу, что в результате предельного перехода в неравенстве (21.9) получим
расходится (пример 2, с. 141 данного пособия). Приходим к выводу, что в результате предельного перехода в неравенстве (21.9) получим 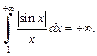 Таким образом, интеграл
Таким образом, интеграл 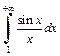 сходится, однако он не сходится абсолютно.
сходится, однако он не сходится абсолютно.
Дата добавления: 2015-09-29; просмотров: 1378;
