Физические приложения определенного интеграла
Путь, пройденный телом со скоростью 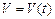 за промежуток времени
за промежуток времени 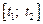
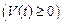 вычисляется по формуле
вычисляется по формуле
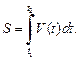 (20.31)
(20.31)
Если материальная точка движется по оси Ox из точки 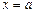 до точки
до точки 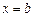 под действием направленной вдоль оси Ox переменной силы F(x), которая задается непрерывной функцией, то работа, произведенная силой F по перемещению точки, вычисляется по формуле
под действием направленной вдоль оси Ox переменной силы F(x), которая задается непрерывной функцией, то работа, произведенная силой F по перемещению точки, вычисляется по формуле
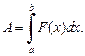 (20.32)
(20.32)
Давление жидкости на погруженную в нее в горизонтальном положении пластинку на глубину h от поверхности жидкости вычисляется по закону Паскаля: 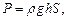 где g – ускорение свободного падения:
где g – ускорение свободного падения: 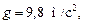 S – площадь пластинки,
S – площадь пластинки, 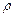 – плотность жидкости. Если пластинка погружена в жидкость в вертикальном положении, то сила давления жидкости на единицу площади изменяется с глубиной погружения. Давление жидкости на вертикальную пластинку, ограниченную линиями
– плотность жидкости. Если пластинка погружена в жидкость в вертикальном положении, то сила давления жидкости на единицу площади изменяется с глубиной погружения. Давление жидкости на вертикальную пластинку, ограниченную линиями 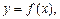
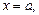
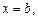
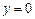 (рис. 20.13), вычисляется по формуле
(рис. 20.13), вычисляется по формуле
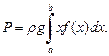 (20.33)
(20.33)
Давление жидкости на вертикальную пластину, ограниченную линиями 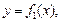
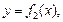
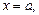
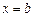 (рис. 20.14), вычисляется по формуле
(рис. 20.14), вычисляется по формуле
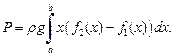 (20.34)
(20.34)

Рис. 20.13 Рис. 20.14
Масса неоднородного стержня, расположенного на отрезке [a; b] оси Ox, имеющего линейную плотность 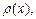 где
где 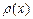 – непрерывная на [a; b] функция, вычисляется по формуле
– непрерывная на [a; b] функция, вычисляется по формуле
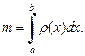 (20.35)
(20.35)
Если дуга плоской кривой задана уравнением 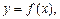 где
где 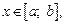 и имеет плотность
и имеет плотность 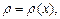
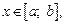 то статистические моменты
то статистические моменты 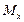 и
и 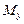 этой дуги относительно координатных осей Ox и Oy вычисляются, соответственно, по формулам:
этой дуги относительно координатных осей Ox и Oy вычисляются, соответственно, по формулам:
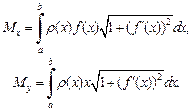 (20.36)
(20.36)
Если кривая задана параметрическими уравнениями 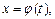
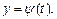
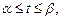 имеет однородную плотность
имеет однородную плотность 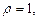 то формулы имеют вид:
то формулы имеют вид:
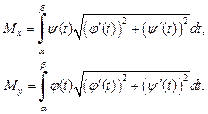 (20.37)
(20.37)
Моменты инерции дуги плоской кривой 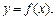 где
где 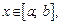 имеющей плотность
имеющей плотность 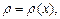 вычисляются по формулам:
вычисляются по формулам:
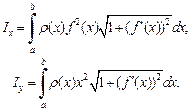 (20.38)
(20.38)
Если кривая задана параметрическими уравнениями 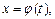
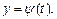
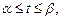
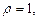 то формулы имеют вид:
то формулы имеют вид:
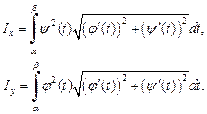 (20.39)
(20.39)
Координаты центра масс дуги плоской кривой 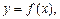 где
где 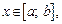 имеющей плотность
имеющей плотность 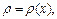 вычисляются по формулам:
вычисляются по формулам:
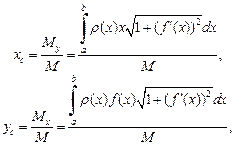 (20.40)
(20.40)
где M – масса дуги: 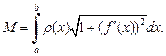
Если кривая задана параметрическими уравнениями 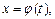
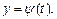
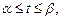
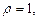 то формулы имеют вид:
то формулы имеют вид:
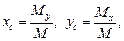 (20.41)
(20.41)
где М – масса дуги: 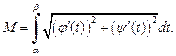
Пример 1.Вычислить площадь криволинейной трапеции, ограниченной линиями:
1) 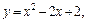
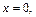
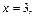
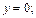
2) 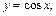
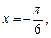
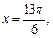
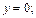
3) 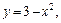
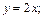
4) 
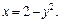
Решение. 1) Построим график функции 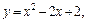 т. е.
т. е. 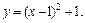 Проведем прямые
Проведем прямые 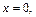
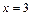 и
и 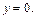 Заштрихуем искомую фигуру (рис. 20.15).
Заштрихуем искомую фигуру (рис. 20.15).
Площадь данной фигуры находим по формуле (20.6)


Рис. 20.15
2) Фигура имеет вид, изображенный на рис. 20.16.

Рис. 20.16
Так как на отрезке 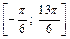 функция принимает значения разных знаков, то разобьем отрезок интегрирования на такие части, где функция принимает значения одного знака. Для нахождения площади фигуры воспользуемся формулами (20.6) и (20.7):
функция принимает значения разных знаков, то разобьем отрезок интегрирования на такие части, где функция принимает значения одного знака. Для нахождения площади фигуры воспользуемся формулами (20.6) и (20.7):
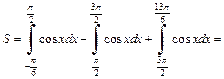
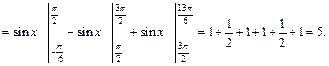
3) Построим графики функций  и
и 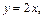 заштрихуем искомую фигуру (рис. 20.17). Найдем пределы интегрирования, т. е. абсциссы точек пересечения графиков функций. Для этого решим систему уравнений
заштрихуем искомую фигуру (рис. 20.17). Найдем пределы интегрирования, т. е. абсциссы точек пересечения графиков функций. Для этого решим систему уравнений 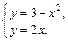

Рис. 20.17
Имеем 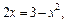
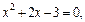
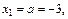

Площадь данной фигуры находим по формуле (20.8)
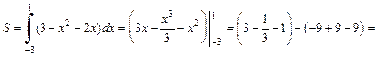
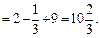
4) Построим графики функции 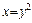 и
и 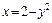 с независимой переменной y. Они образуют плоскую фигуру (рис. 20.18). Найдем ординаты точек пересечения графиков данных функций. Для этого решим систему уравнений
с независимой переменной y. Они образуют плоскую фигуру (рис. 20.18). Найдем ординаты точек пересечения графиков данных функций. Для этого решим систему уравнений 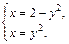
Имеем 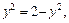
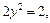
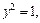
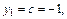

Площадь данной фигуры находим по формуле (20.10)
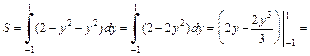
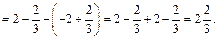

Рис. 20.18
Пример 2. Найти площадь фигуры, ограниченной линиями:
1) эллипсом 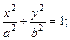
2) первой аркой циклоиды 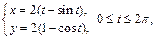 и прямой
и прямой 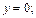
3) кардиоидой 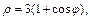
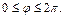
Решение. 1) Запишем уравнение эллипса в параметрическом виде
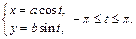
Эллипс – симметричная кривая. В основу вычисления положим площадь фигуры, лежащей в первой координатной четверти, образованной эллипсом и координатными осями (рис. 20.19). Она проектируется на отрезок [0; 2] оси Ox. Найдем пределы интегрирования: если 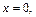 то
то 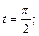 если
если 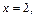 то
то 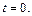 Поэтому воспользуемся формулой (20.11) для вычисления площади фигуры
Поэтому воспользуемся формулой (20.11) для вычисления площади фигуры
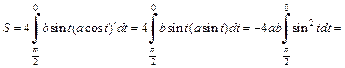
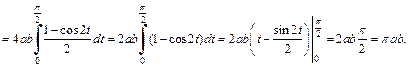
2) Фигура, ограниченная аркой циклоиды и осью Ox, изображена на рис. 20.20.

Рис. 20.19

Рис. 20.20
Найдем пределы интегрирования: если 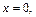 то
то 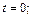 если
если 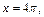 то
то 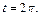
Найдем площадь фигуры по формуле (20.11)
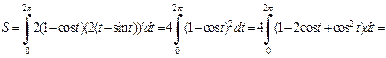
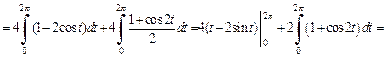
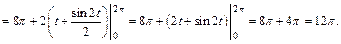
3) Кардиоида образует фигуру, симметричную относительно оси Ox (рис. 20.21).
Используя симметрию, найдем площадь фигуры по формуле (20.12)
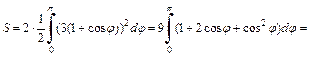

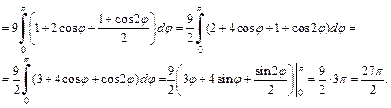
Рис. 20.21
Пример 3. Вычислить длину дуги кривой:
1) 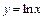 от точки с абсциссой 1 до точки с абсциссой
от точки с абсциссой 1 до точки с абсциссой 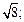
2) 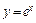 от точки
от точки 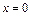 до точки
до точки 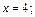
3) 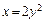 от точки
от точки 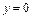 до
до 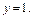
Решение. 1) Применим формулу (20.14). Для 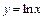 имеем
имеем 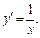 Получаем:
Получаем:
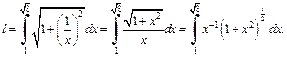
Подынтегральное выражение является дифференциальным биномом. Поскольку 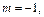
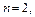
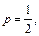
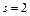 и
и 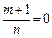 – целое число, то используем подстановку
– целое число, то используем подстановку 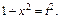 Тогда
Тогда 
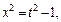
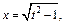
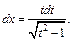 Если
Если 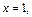 то
то 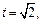 если
если 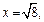 то
то 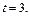
Получим:
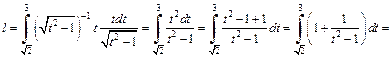

2) Применим формулу (20.14). Для функции 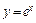 имеем
имеем 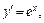 поэтому
поэтому
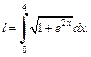
Используем подстановку  Тогда
Тогда 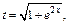
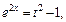
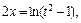
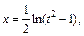
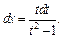
Находим новые пределы интегрирования: если 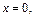 то
то 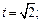 если
если 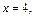 то
то 
Получаем:
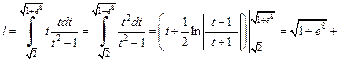
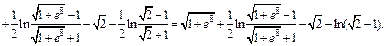
3) Применим формулу (20.15). Для функции 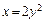 имеем
имеем 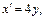 тогда
тогда 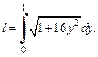
Вычислим интеграл методом интегрирования по частям:
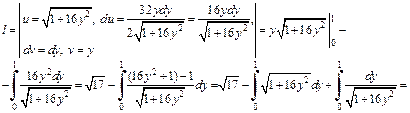
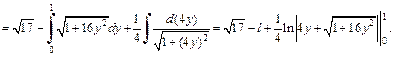
Найдем длину дуги l из полученного равенства:
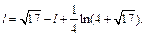
Выражаем:

Пример 4. Найти длину:
1) астроиды 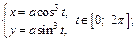
2) дуги розы 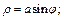
3) первого витка спирали Архимеда 
4) дуги логарифмической спирали 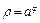
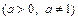 между точками
между точками 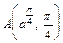 и
и 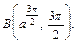
Решение. 1) Применим формулу (20.16). Астроида – симметричная кривая (рис. 20.22).

Рис. 20.22
Вычислим длину дуги, лежащей в первой координатной четверти. Тогда для 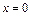 имеем
имеем 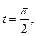 для
для 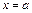 имеем
имеем 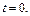 Вычисляем производные:
Вычисляем производные:
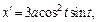
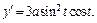
Получаем:
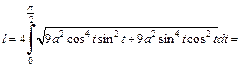
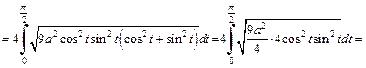
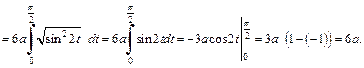
2) Кривая, определяемая уравнением 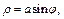 имеет один лепесток (рис. 20.23).
имеет один лепесток (рис. 20.23).

Рис. 20.23
Длину дуги лепестка получим, если φ изменяется от 0 до π. Применим формулу (20.18). Вычислим производную: 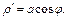
Получаем: 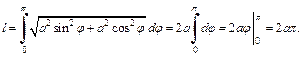
3) Длину первого витка спирали Архимеда (рис. 20.24) получим, если φ изменяется от 0 до 2π. Применим формулу (20.18). Поскольку 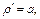 то получаем:
то получаем:
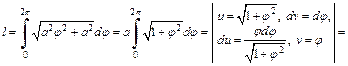
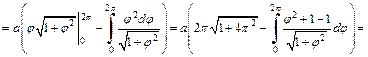
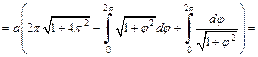
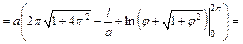
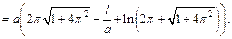
Найдем длину дуги l из полученного равенства
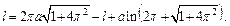
Выражаем:
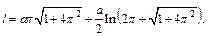

Рис. 20.24
4) Логарифмическая спираль 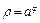 изображена на рис. 20.25. Применим формулу (20.18). Точку
изображена на рис. 20.25. Применим формулу (20.18). Точку 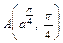 получим, если
получим, если 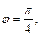 точку
точку 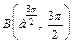 получим, если
получим, если 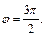 Поэтому имеем:
Поэтому имеем:
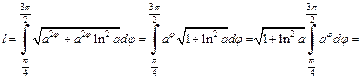
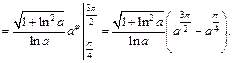

Рис. 20.25
Пример 5. Найти объем тела, ограниченного эллиптическим параболоидом 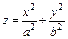 и плоскостью
и плоскостью 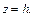
Решение. Если эллиптический параболоид 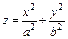 пересечь плоскостью
пересечь плоскостью 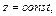 то в его сечении получим эллипс
то в его сечении получим эллипс 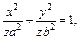 т. е.
т. е. 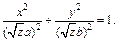 Площадь эллипса найдена в примере 2 (см. с. 115). Имеем
Площадь эллипса найдена в примере 2 (см. с. 115). Имеем 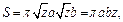
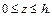 Для вычисления объема тела применим формулу (20.19):
Для вычисления объема тела применим формулу (20.19): 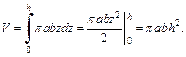
Пример 6. Используя определенный интеграл, получить формулу объема шара двумя способами.
Решение. 1-й способ. Поместим центр шара в начало координат (рис. 20.26). Пересечем шар плоскостью, перпендикулярной оси Ox. Вычислим площадь круга, полученного в сечении. Обозначим его радиус через r. Тогда 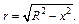 Площадь круга является функцией переменной x и равна
Площадь круга является функцией переменной x и равна 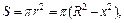 причем x изменяется от – R до R. Для вычисления объема шара применим формулу (20.19):
причем x изменяется от – R до R. Для вычисления объема шара применим формулу (20.19):
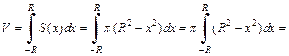
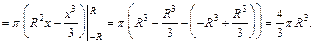
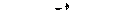
Рис. 20.26
2-й способ. Вычислим объем шара, рассматривая его как тело вращения. Пусть окружность 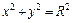 вращается вокруг оси Ox, она образует сферическую поверхность, которая является границей шара. Для вычисления объема шара применим формулу (20.20). Поскольку
вращается вокруг оси Ox, она образует сферическую поверхность, которая является границей шара. Для вычисления объема шара применим формулу (20.20). Поскольку 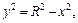 где
где 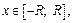 то получаем формулу объема шара:
то получаем формулу объема шара:
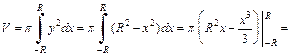
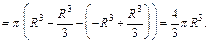
Пример 7. Используя определенный интеграл, получить формулу площади поверхности сферы.
Решение. Вычислим площадь поверхности сферы по формуле (20.21). Так как 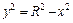 (рис. 20.26), то
(рис. 20.26), то
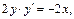
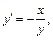
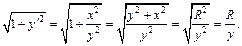
Тогда 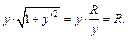
Получаем формулу площади поверхности сферы:
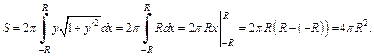
Пример 8. Найти объем тела:
1) образованного вращением вокруг оси Ox параболы 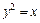 и ограниченного плоскостью
и ограниченного плоскостью 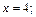
2) образованного вращением фигуры, ограниченной линиями 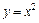 и
и 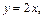 вокруг оси Oy.
вокруг оси Oy.
Решение. 1) Для вычисления объема тела (рис. 20.27) применим формулу (20.20):
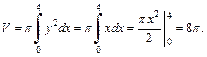
Площадь боковой поверхности вычислим по формуле (20.21). Выразив y через x, получим 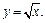
Находим:
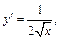 и
и 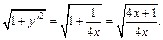
Тогда
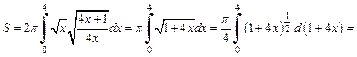


Рис. 20.27
2) Построим графики функций 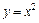 и
и 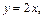 заштрихуем образованную ими плоскую фигуру (рис. 20.28). Найдем пределы интегрирования, т. е. ординаты точек пересечения графиков функций. Для этого решим систему уравнений
заштрихуем образованную ими плоскую фигуру (рис. 20.28). Найдем пределы интегрирования, т. е. ординаты точек пересечения графиков функций. Для этого решим систему уравнений 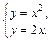

Рис. 20.28
Имеем: 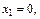
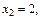 тогда
тогда 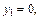
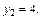 Представив заданные функции как функции переменной у, получим:
Представив заданные функции как функции переменной у, получим: 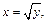
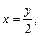 где
где 
Объем тела, полученного вращением плоской фигуры вокруг оси Oy, вычислим по формуле (20.26):

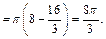
Пример 9. Найти объем и площадь поверхности тела, образованного вращением:
1) одной арки циклоиды
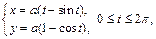 вокруг оси Ox;
вокруг оси Ox;
2) кардиоиды  вокруг полярной оси.
вокруг полярной оси.
Решение. 1) Объем тела и площадь поверхности вычислим по формулам (20.27) и (20.28).
Находим: 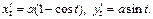
Тогда
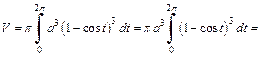
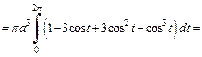
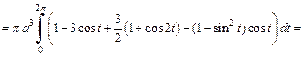
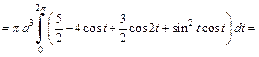
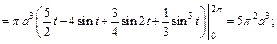
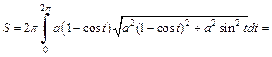
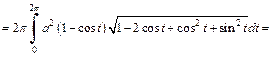
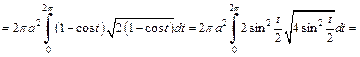
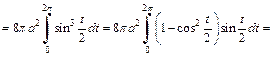
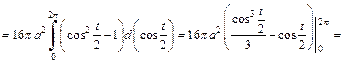
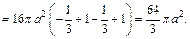
2) Объем тела, образованного вращением кардиоиды вокруг полярной оси, вычислим по формулам (20.29) и (20.30) и учтем, что кардиоида – фигура, симметричная относительно полярной оси (поэтому 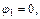
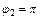 – пределы интегрирования).
– пределы интегрирования).
Вычисляем 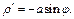 Тогда
Тогда
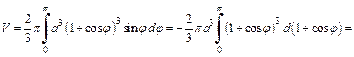
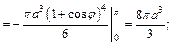
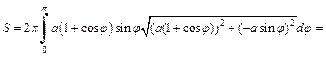
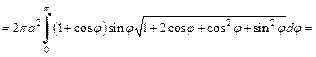
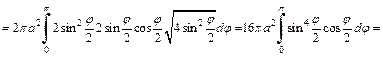
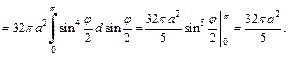
Пример 10. Найти силу давления жидкости на пластину, вертикально погруженную в жидкость, если пластина имеет форму полукруга радиусом R, диаметр которого находится на поверхности воды (рис. 20.29).

Рис. 20.29
Решение. Давление жидкости на полукруг ABC численно равно удвоенному давлению испытываемому четвертью круга OBC. Уравнение дуги BC имеет вид: 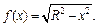 Тогда по формуле (20.33) находим искомое давление
Тогда по формуле (20.33) находим искомое давление
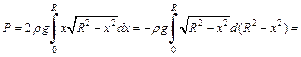
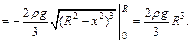
Пример 11. Найти координаты центра масс однородной дуги 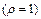 астроиды
астроиды 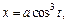
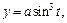 расположенной в первой четверти.
расположенной в первой четверти.
Решение. Координаты 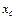 и
и 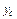 находим по формулам (20.41). Имеем
находим по формулам (20.41). Имеем 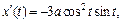
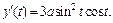 Так как
Так как 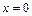 при
при 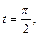
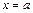 при
при 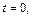 то по формулам (20.37) получаем:
то по формулам (20.37) получаем:
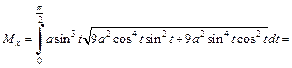
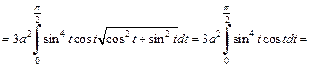
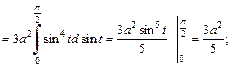
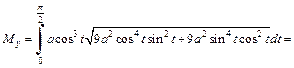
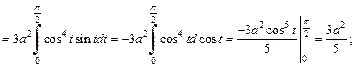
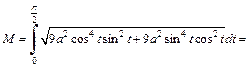
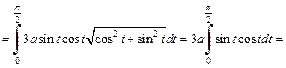
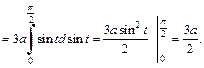
Тогда 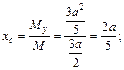
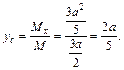
Следовательно, центр масс имеет координаты 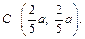
Пример 12. Скорость автомобиля при торможении меняется по закону  (м/с). Определить, какой путь (м) пройдет автомобиль от начала торможения до полной остановки.
(м/с). Определить, какой путь (м) пройдет автомобиль от начала торможения до полной остановки.
Решение. Путь, пройденный автомобилем, вычислим по формуле (20.31). Найдем время от начала торможения 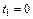 до остановки
до остановки 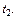 Из равенства
Из равенства 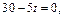 находим
находим 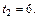 Поэтому
Поэтому
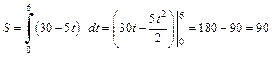 (м).
(м).
Дата добавления: 2015-09-29; просмотров: 3328;
