Объем и площадь поверхности тела вращения

Если тело ограничивает поверхность, полученную вращением кривой 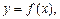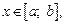вокруг оси Ox (рис. 20.11), то его объем вычисляется по формуле

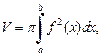(20.20)

а площадь поверхности – по формуле

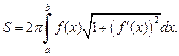(20.21)

Если тело ограничено поверхностью, которая образована вращением кривой 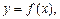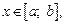вокруг оси Oy, то его объем вычисляется по формуле

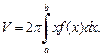(20.22)

Если тело ограничено поверхностью, полученной вращением кривой 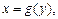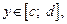вокруг оси Oy (рис. 20.12), то его объем вычисляется по формуле

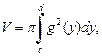(20.23)

а площадь поверхности – по формуле

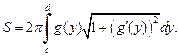(20.24)

Рис. 20.11 Рис. 20.12

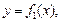
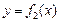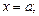
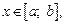Если плоская фигура, ограниченная кривыми и прямыми для вращается вокруг оси Ox, то объем тела вращения вычисляется по формуле

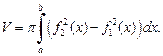(20.25)

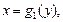
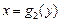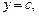
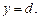
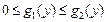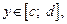Если плоская фигура, ограниченная кривыми и прямыми для вращается вокруг оси Oy, то объем тела вращения вычисляется по формуле

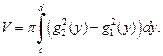(20.26)

Если кривая, заданная параметрическими уравнениями 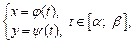вращается вокруг оси Ox, то объем тела вращения вычисляется по формуле

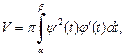(20.27)

а площадь поверхности вращения – по формуле

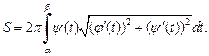(20.28)

Если тело получено вращением сектора, ограниченного кривой 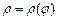и лучами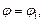 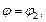вокруг полярной оси, то его объем вычисляется по формуле

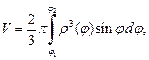(20.29)

а площадь поверхности – по формуле

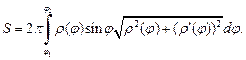(20.30)