Площадь плоской фигуры

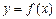
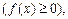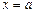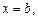Площадь криволинейной трапеции, ограниченной сверху графиком непрерывной функции слева и справа, соответственно, прямыми и снизу – отрезком [a; b] оси Ox (рис. 20.3), выражается формулой

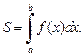(20.6)

Есл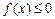и при 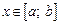(рис. 20.4), то

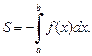(20.7)

Рис. 20.3 Рис. 20.4

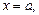
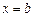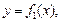
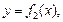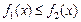Площадь криволинейной трапеции, ограниченной прямыми и кривыми где для 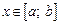(рис. 20.5), выражается формулой

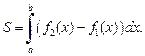(20.8)

Площадь криволинейной трапеции, ограниченной прямыми 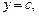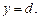кривой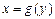 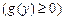и отрезком [c; d] оси Oy (рис. 20.6), выражается формулой

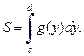(20.9)

Рис. 20.5 Рис. 20.6

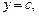
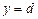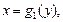
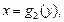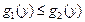Площадь криволинейной трапеции, ограниченной прямыми и кривыми где для 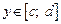(рис. 20.7), выражается формулой

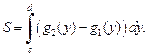(20.10)

Рис. 20.7

Если криволинейная трапеция ограничена сверху кривой, заданной параметрическими уравнениями

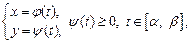
прямыми 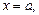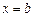и отрезком [a; b] оси Ox, то ее площадь вычисляется по формуле

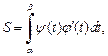(20.11)

где 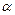и 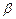определяются из равенств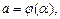

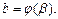
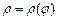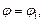
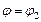
Площадь криволинейного сектора, ограниченного кривой, заданной в полярных координатах уравнением и двумя лучами 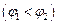(рис. 20.8), причем 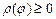для 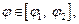выражается формулой

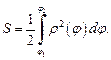(20.12)

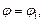
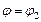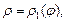
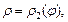
Площадь плоской фигуры, ограниченной двумя лучами и кривыми 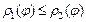для 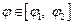(рис. 20.9), выражается формулой

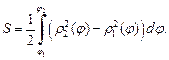(20.13)

Рис. 20.8 Рис. 20.9