Замена переменной в определенном интеграле
Пусть f (x) – непрерывная на отрезке [a; b] функция, а функция 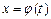 и ее производная
и ее производная 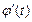 непрерывны на отрезке
непрерывны на отрезке 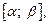 где
где 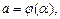
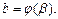 Тогда справедлива формула
Тогда справедлива формула
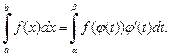 (20.5)
(20.5)
Вместе с заменой переменной в определенном интеграле заменяются пределы интегрирования.
Пример 1. Вычислить интеграл:
1) 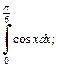 2)
2) 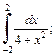
3) 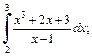 4)
4) 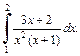
Решение. 1) Применим формулу Ньютона-Лейбница (20.3):
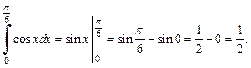
2) Подынтегральная функция 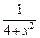 является четной. Поэтому
является четной. Поэтому
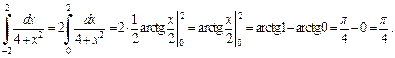
3) Подынтегральная функция является неправильной рациональной дробью. Выделим целую часть, разделив ее числитель на знаменатель по правилу деления многочленов:
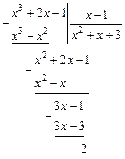
Тогда
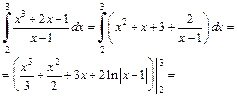
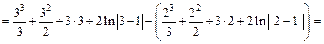
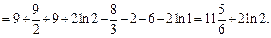
4) Подынтегральная функция является правильной рациональной дробью. Разложим ее на сумму простейших дробей:
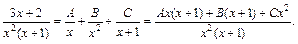
Найдем коэффициенты A, B, C из равенства
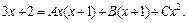
Полагая 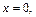 получаем
получаем 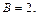 При
При 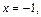 получаем
получаем 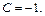 Полагая
Полагая 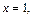 получаем
получаем 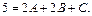 Далее находим:
Далее находим: 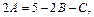
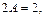 т. е.
т. е. 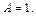
Тогда
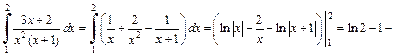
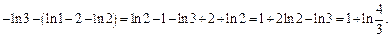
Пример 2. Вычислить интеграл, используя формулу интегрирования по частям:
1) 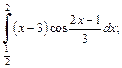 2)
2) 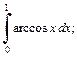
3) 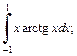 4)
4) 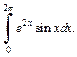
Решение. 1) По формуле (20.4) имеем:
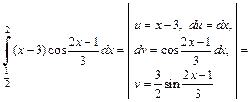
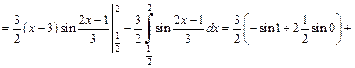
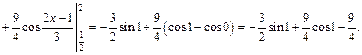
2) Используем формулу (20.4):
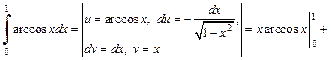
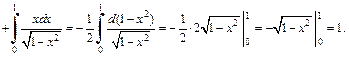
3) Подынтегральная функция является четной, поэтому
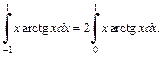
Применим формулу (20.4) интегрирования по частям. Пусть 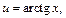
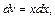
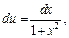
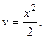
Получим:
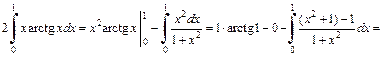
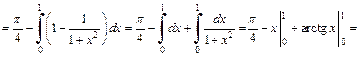
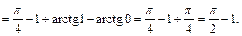
4) Используем формулу (20.4) интегрирования по частям дважды:
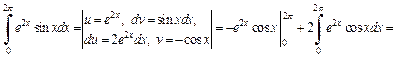
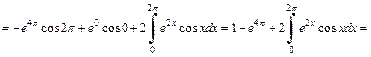
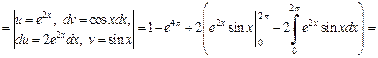
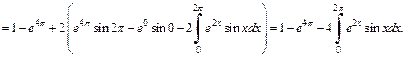
Таким образом, получили равенство
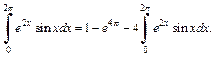
Из него находим:
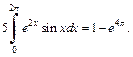
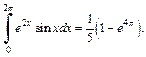
Пример 3. Вычислить определенный интеграл, используя формулу замены переменной:
1) 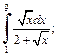 2)
2) 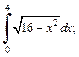 3)
3) 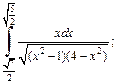
4) 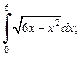 5)
5) 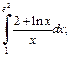 6)
6) 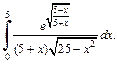
Решение. 1) Сделаем подстановку 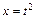
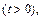 тогда
тогда 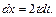 Определим новые пределы интегрирования. Для этого в равенство замены переменной поочередно подставим
Определим новые пределы интегрирования. Для этого в равенство замены переменной поочередно подставим 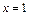 (заданный нижний предел интегрирования) и
(заданный нижний предел интегрирования) и 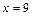 (заданный верхний предел): если
(заданный верхний предел): если 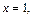 то
то 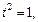
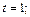 если
если 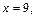 то
то 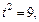
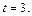
Используем формулу (20.5) замены переменной в определенном интеграле:
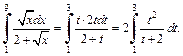
Получили интеграл от неправильной рациональной дроби. Выделим целую часть в подынтегральном выражении:
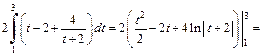
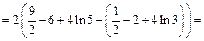
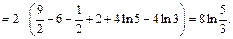
2) 1-й способ. Используем метод подстановки. Положим 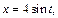 тогда
тогда 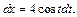
Найдем новые пределы интегрирования: если 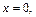 то
то 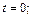 если
если 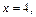 то
то 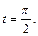
Следовательно,
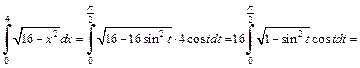
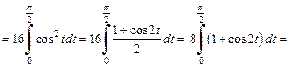
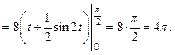
2-й способ. Используем формулу (20.4) интегрирования по частям.
Положим 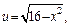
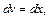 тогда
тогда 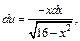
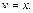
Получаем:
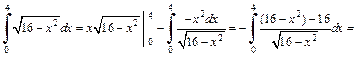
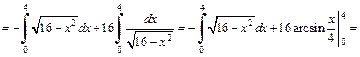
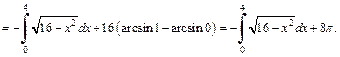
Найдем искомый интеграл из полученного равенства
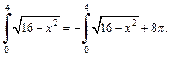
Выражаем:
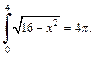
3) Применим подстановку 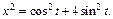
Тогда 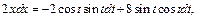 т. е.
т. е. 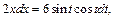
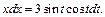
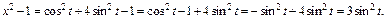
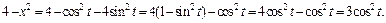
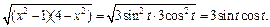
Таким образом, подынтегральное выражение примет вид:
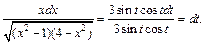
Определим новые пределы интегрирования: если 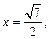 то
то 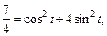 т. е.
т. е. 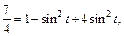
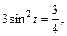
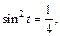
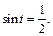 Находим
Находим 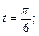
если 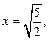 то
то 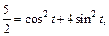 т. е.
т. е. 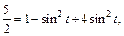
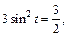
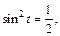
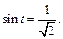 Находим
Находим 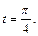
Получаем:
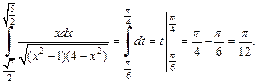
4) В подкоренном выражении выделим полный квадрат:
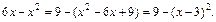
Применим подстановку 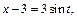
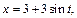
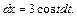
Определим новые пределы интегрирования: если 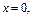 то
то 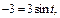
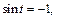
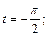 если
если 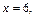 то
то 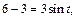
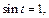
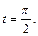
Получаем:
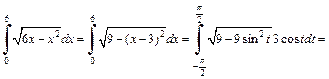
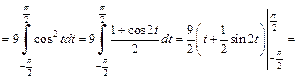
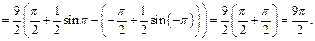
5) 1-й способ. Используем метод замены переменной. Положим 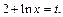 Тогда
Тогда 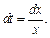
Находим новые пределы интегрирования, используя равенство замены переменной: если 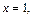 то
то 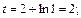 если
если 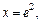 то
то 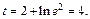
Получим:
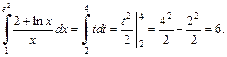
2-й способ. Используем метод поднесения под знак дифференциала:
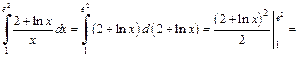
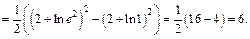
Заметим, что в случае использования метода поднесения под знак дифференциала не нужно изменять пределы интегрирования, а поэтому, как правило, он является более рациональным.
6) Применим подстановку:
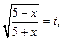 тогда
тогда 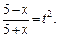
Выразим переменную x через t:
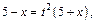
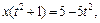
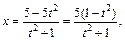
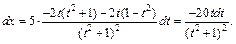
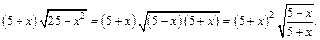
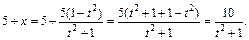
Определим новые пределы интегрирования: если 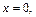 то
то 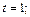 если
если 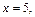 то
то 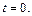
Используя формулу (20.5) замены переменной в определенном интеграле, получаем:
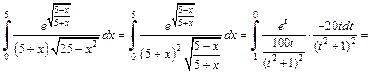
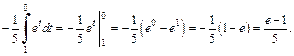
Дата добавления: 2015-09-29; просмотров: 1178;
