Понятие определенного интеграла и его свойства
Пусть на отрезке [a; b], (всюду 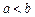 ) определена непрерывная ограниченная функция f (x). Произвольным образом разобьем отрезок [a; b] на n отрезков точками
) определена непрерывная ограниченная функция f (x). Произвольным образом разобьем отрезок [a; b] на n отрезков точками 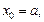
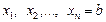
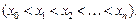 Полученные отрезки
Полученные отрезки 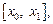
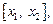 …
… 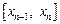 будем называть частичными. Длину k-го частичного отрезка
будем называть частичными. Длину k-го частичного отрезка 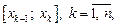 обозначим
обозначим 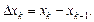 На каждом частичном отрезке выберем произвольную точку
На каждом частичном отрезке выберем произвольную точку 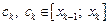 (рис. 20.1) и вычислим значение функции в этой точке, т. е.
(рис. 20.1) и вычислим значение функции в этой точке, т. е. 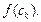

Рис. 20.1
Для каждого k, 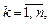 найдем произведение
найдем произведение 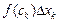 и составим сумму:
и составим сумму:
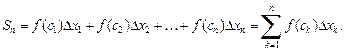 (20.1)
(20.1)
Сумма (20.1) называется интегральной суммой функции f (x) на отрезке [a; b].
Обозначим через 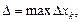
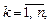 длину наибольшего частичного отрезка.
длину наибольшего частичного отрезка.
Будем рассматривать всевозможные разбиения отрезка [a; b] при условии, что 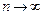 и
и 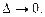
Определение. Если существует предел интегральной суммы (20.1) при 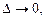 который не зависит ни от способа разбиения отрезка
который не зависит ни от способа разбиения отрезка 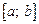 на частичные отрезки, ни от выбора точек
на частичные отрезки, ни от выбора точек 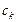 на каждом частичном отрезке, то этот предел называется определенным интегралом функции f (x) на отрезке [a; b] и обозначается
на каждом частичном отрезке, то этот предел называется определенным интегралом функции f (x) на отрезке [a; b] и обозначается 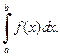
Таким образом,
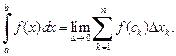 (20.2)
(20.2)
Числа a и b в формуле (20.2) называются соответственно нижним и верхним пределами интегрирования. Функция f (x) называется подынтегральной функцией, f (x)dx – подынтегральным выражением, x – переменной интегрирования, отрезок [a; b] – отрезком интегрирования.
Функция f (x), для которой существует интеграл (20.2), называется интегрируемой на отрезке.
Классы интегрируемых функций:
1) непрерывная на отрезке [a; b] функция интегрируема;
2) ограниченная на отрезке [a; b] функция, имеющая лишь конечное число точек разрыва, интегрируема;
3) монотонная ограниченная функция интегрируема.
Если 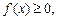
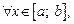 то фигура, ограниченная графиком функции
то фигура, ограниченная графиком функции 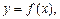 осью Ox, прямыми
осью Ox, прямыми 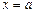 и
и 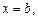 называется криволинейной трапецией (рис. 20.1).
называется криволинейной трапецией (рис. 20.1).
Геометрический смысл определенного интеграла: определенный интеграл (20.2) от неотрицательной функции численно равен площади криволинейной трапеции.
Физический смысл определенного интеграла: пусть материальная точка M движется вдоль числовой оси со скоростью V(t), 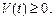 Тогда путь, пройденный точкой за промежуток времени от
Тогда путь, пройденный точкой за промежуток времени от 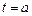 до
до 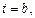 равен определенному интегралу от скорости:
равен определенному интегралу от скорости:
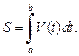
Дата добавления: 2015-09-29; просмотров: 896;
