Вычисление площади плоской фигуры.
НЕКОТОРЫЕ ГЕОМЕТРИЧЕСКИЕ И МЕХАНИЧЕСКИЕ
ПРИЛОЖЕНИЯ ОПРЕДЕЛЁННОГО ИНТЕГРАЛА.
Вычисление площади плоской фигуры.
Определённый интеграл позволяет вычислять площади самых различных плоских фигур.
1.В прямоугольной системе координат XOY. За основную фигуру здесь принимается криволинейная трапеция, так как её площадь выражается одним




 определённым интегралом.
определённым интегралом. 
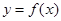 B
B






 а) мы видим, что если
а) мы видим, что если 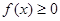 на [a, b], то
на [a, b], то 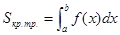 ; A
; A
 b) если
b) если 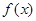 непрерывна и
непрерывна и 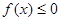 на [a, b], то имеем также
на [a, b], то имеем также 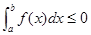 . 0
. 0 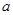
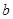










 По абсолютной величине он равен площади соответствующей криволинейой
По абсолютной величине он равен площади соответствующей криволинейой 
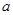
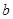



 трапеции
трапеции 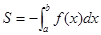 , т.е.
, т.е. 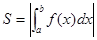 - эта формула справедлива в B
- эта формула справедлива в B
обоих случаях а) и b). A


 c)
c) 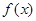 непрерывна и несколько раз пересекает ось OX. Этот случай сводится к двум рассмотренным и b).
непрерывна и несколько раз пересекает ось OX. Этот случай сводится к двум рассмотренным и b). 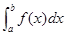 в этом случае даёт разность
в этом случае даёт разность 









 площадей, лежащих выше и ниже оси OX. Чтобы найти
площадей, лежащих выше и ниже оси OX. Чтобы найти 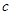
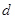
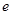

 площадь заштрихованной фигуры, нужно учесть знаки:
площадь заштрихованной фигуры, нужно учесть знаки: 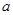
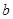




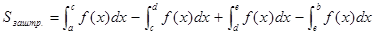 или
или

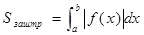
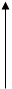
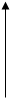 d) На [a, b] определены две непрерывные функции
d) На [a, b] определены две непрерывные функции 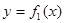 и
и 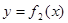 , причём
, причём 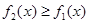 .
.
























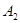
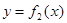
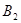

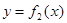







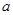
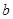



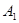
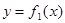
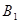
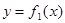
0 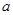
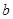





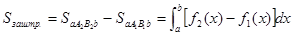 ,
, 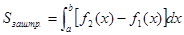
Нужно заметить, что эта формула справедлива при любом расположении кривых 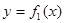 и
и



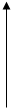

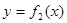 , лишь бы
, лишь бы 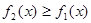 .
. 
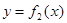
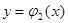





 Замечание 1. Если контур фигуры состоит из кусков, задаваемых
Замечание 1. Если контур фигуры состоит из кусков, задаваемых



 разными фигурами, то фигуру разбивают на части рассмотренного
разными фигурами, то фигуру разбивают на части рассмотренного 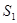
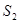



 вида прямыми, параллельными координатным осям. Тогда
вида прямыми, параллельными координатным осям. Тогда 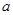
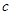
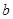

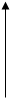 (см. рис.)
(см. рис.) 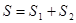 .
. 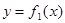
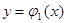




 Замечание 2. Все формулы и их обоснование верны и в том
Замечание 2. Все формулы и их обоснование верны и в том 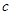 C
C

 случае, когда имеем дело с криволинейными трапециями, основания
случае, когда имеем дело с криволинейными трапециями, основания 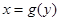


 которых
которых 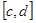 на оси OY, и они ограниченны кривыми
на оси OY, и они ограниченны кривыми 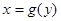 , так,
, так, 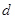 D
D
например: 0 
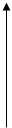




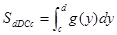



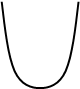



 Пример. Вычислить площадь параболического сегмента, ограниченного A 2 B
Пример. Вычислить площадь параболического сегмента, ограниченного A 2 B 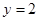
параболой 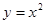 и прямой
и прямой 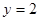 .
. 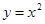
 Решение. Найдём координаты точек пересечения кривых A и B.
Решение. Найдём координаты точек пересечения кривых A и B.

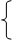
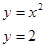 =>
=> 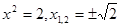 =>
=> 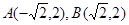 .
. 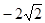 0
0 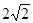

Тогда:
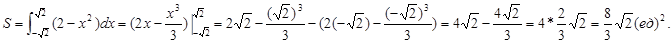
 2. Параметрическое задание линий контура фигуры.
2. Параметрическое задание линий контура фигуры. 










 Пусть кривая AB, ограничивающая криволинейную трапецию aABb, A B
Пусть кривая AB, ограничивающая криволинейную трапецию aABb, A B
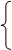
 задана в параметрической форме:
задана в параметрической форме: 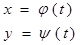 ,
, 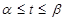 , причём
, причём
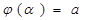 и
и 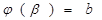 . 0
. 0 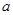
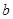

Тогда на 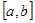 эти параметрические уравнения определяют некоторую функцию
эти параметрические уравнения определяют некоторую функцию 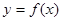 и по 1 пункту имеем:
и по 1 пункту имеем: 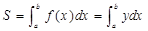 .
.


 Сделаем замену переменной в этом интеграле:
Сделаем замену переменной в этом интеграле: 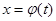 . Тогда
. Тогда 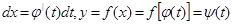 , и мы получим:
, и мы получим: 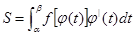 или
или

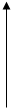


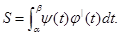




 Пример. Вычислить площадь, ограниченную эллипсом:
Пример. Вычислить площадь, ограниченную эллипсом: 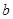


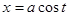 ,
, 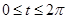 . 0
. 0 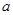

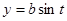

Решение. В силу симметрии эллипса вычислим площадь одной четверти эллипса (в 1 - ой четверти) и умножим на 4, при этом t будет меняться от t = 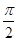 до 0(
до 0( 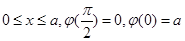 ).Поэтому:
).Поэтому: 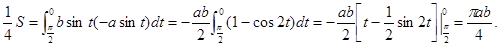 Тогда
Тогда 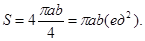
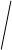



 3. Площадь фигуры в полярной системе координат. A
3. Площадь фигуры в полярной системе координат. A


 Если контур, ограничивающий фигуру, задан в полярной
Если контур, ограничивающий фигуру, задан в полярной

 системе координат, то в качестве основной фигуры берут
системе координат, то в качестве основной фигуры берут



 криволинейный сектор — фигуру, ограниченную двумя
криволинейный сектор — фигуру, ограниченную двумя 


 полярными радиусами
полярными радиусами 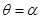 и
и 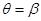 и непрерывной кривой
и непрерывной кривой 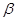
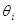
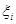 B
B

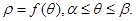 Найдём площадь этого сектора. 0
Найдём площадь этого сектора. 0 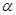

Разобьём 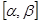 на части точками
на части точками 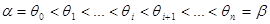 и проведём соответствующие этим углам
и проведём соответствующие этим углам 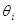 полярные радиусы. Тогда весь сектор разобьётся на n элементарных секторов. Заменим каждый элементарный криволинейный сектор круговым с
полярные радиусы. Тогда весь сектор разобьётся на n элементарных секторов. Заменим каждый элементарный криволинейный сектор круговым с
радиусом 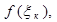 где
где 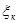 -- произвольная точка на
-- произвольная точка на 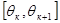 . Площадь кругового сектора радиуса
. Площадь кругового сектора радиуса 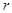 с центральным углом
с центральным углом 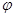 равна
равна 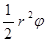 . Поэтому площадь полученной ступенчатой фигуры из
. Поэтому площадь полученной ступенчатой фигуры из 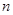 круговых секторов будет равна:
круговых секторов будет равна: 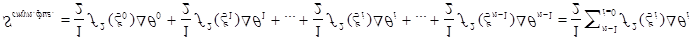 здесь
здесь 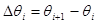 .
.
Чем мельче дробление, тем ближе ступенчатая формула подходит к криволинейному сектору, потому за площадь криволинейного сектора естественно принять предел площади ступенчатой фигуры, когда 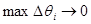 :
:
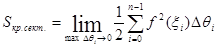 , но этот предел есть неопределённый интеграл. Поэтому:
, но этот предел есть неопределённый интеграл. Поэтому:








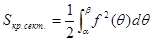 или
или 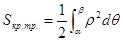
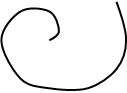
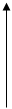 Пример. Вычислить площадь фигуры, ограниченной одним витком
Пример. Вычислить площадь фигуры, ограниченной одним витком

 спирали Архимеда
спирали Архимеда 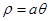 и полярной осью.
и полярной осью.



 Решение.
Решение. 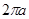

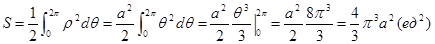 .
. 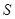
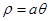
Замечание. В случае, указанном на рисунке:







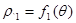
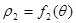







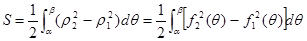 .
. 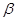
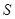
 0
0 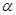

§2. Вычисление объёмов некоторых видов тел.


 Рассмотрим несколько случаев.
Рассмотрим несколько случаев.
a) 
 Тело (
Тело ( 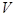 ) есть прямой цилиндр, основанием которого является S
) есть прямой цилиндр, основанием которого является S

 фигура (
фигура ( 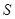 ),
), 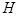 – высота. Будем рассматривать все возможные вписанные
– высота. Будем рассматривать все возможные вписанные


 в основание многоугольники (
в основание многоугольники ( 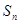 ) и на каждом из них строим вписанную
) и на каждом из них строим вписанную
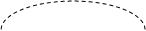
 в цилиндр прямую призму. При измельчении сторон многоугольников H
в цилиндр прямую призму. При измельчении сторон многоугольников H
( 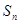 ) прямые призмы всё теснее прижимаются к цилиндру. Поэтому
) прямые призмы всё теснее прижимаются к цилиндру. Поэтому
 естественно принять за объём
естественно принять за объём 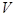 цилиндра предел, к которому
цилиндра предел, к которому
стремятся объёмы вписанных призм 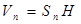 при
при 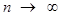 и
и


 длине сторон, стремящейся к нулю. Но при этом
длине сторон, стремящейся к нулю. Но при этом 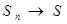 и потому
и потому 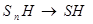 . Таким образом, объём прямого цилиндра
. Таким образом, объём прямого цилиндра 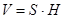 .
.
 b) Пусть дано тело (
b) Пусть дано тело ( 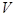 ), ограниченное замкнутой поверхностью, а слева и справа плоскостями
), ограниченное замкнутой поверхностью, а слева и справа плоскостями 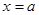 и
и 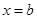 .
.







 Известна площадь любого его сечения, произведённого плоскостью, перпендикулярной к оси
Известна площадь любого его сечения, произведённого плоскостью, перпендикулярной к оси 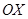 (поперечное сечение тела (
(поперечное сечение тела ( 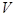 )).
)).

 Можно считать, что площадь любого поперечного сечения
Можно считать, что площадь любого поперечного сечения 









 является функцией от
является функцией от 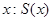 (
(  — абсцисса точки
— абсцисса точки
пересечения плоскости с осью 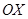 ),
), 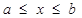 .
.
Будем предполагать тело ( 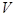 ) таким, что функция
) таким, что функция 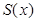




 непрерывна на
непрерывна на 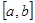 .
.


 Для определения объёма такого тела рассуждаем следующим 0
Для определения объёма такого тела рассуждаем следующим 0 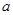
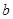

 образом: разобьём
образом: разобьём 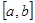 на элементарные точками
на элементарные точками 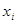
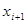

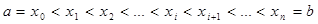 и через них
и через них 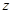
проведём поперечные сечения. Тело ( 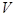 ) разобьётся на
) разобьётся на 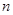 слоёв. Каждый
слоёв. Каждый 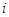 - й слой (см. рис.) заменим прямым цилиндром с той же высотой
- й слой (см. рис.) заменим прямым цилиндром с той же высотой 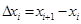 и основанием
и основанием 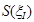 ,
, 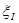 — произвольная точка на
— произвольная точка на 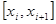 . Объём
. Объём 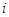 - ого прямого цилиндра
- ого прямого цилиндра 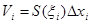 . Тогда объём ступенчатого тела(из прямых цилиндров) будет:
. Тогда объём ступенчатого тела(из прямых цилиндров) будет: 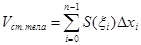 .
.
Перейдём к пределу при 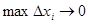 . С одной стороны это будет объём данного тела (
. С одной стороны это будет объём данного тела ( 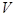 ), а с
), а с
другой — это предел интегральной суммы для непрерывной функции 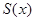 на
на 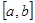 , т.е.
, т.е. 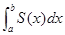 . Таким образом, имеем:
. Таким образом, имеем: 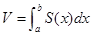 .
.
Это формула объёма тела по известным площадям поперечных сечений.
с) Пусть тело (  ) есть тело вращения. Оно получается вращением
) есть тело вращения. Оно получается вращением
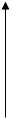 около оси
около оси 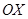 криволинейной трапеции
криволинейной трапеции 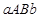 , ограниченной
, ограниченной 


 сверху графиком непрерывной функции
сверху графиком непрерывной функции 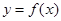 . Такое тело
. Такое тело 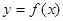 B
B
 полностью удовлетворяет пункту b). Причём, площадь любого A
полностью удовлетворяет пункту b). Причём, площадь любого A
поперечного сечения (как круга радиуса 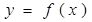 )
) 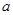


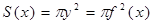 — непрерывная функция от
— непрерывная функция от  . Тогда: 0
. Тогда: 0 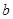










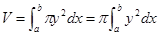 или
или 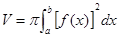 .
.
Это и есть формула объёма тела вращения (около оси 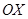 ).
).


 Если криволинейная трапеция ограничена двумя кривыми
Если криволинейная трапеция ограничена двумя кривыми 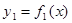 и
и 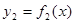 , и
, и 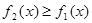 на
на 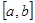 , то очевидно:
, то очевидно:
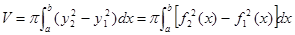
 Совершенно аналогичными рассуждениями можно получить объём
Совершенно аналогичными рассуждениями можно получить объём 
 тела вращения около оси
тела вращения около оси 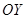 , если вращается непрерывная кривая
, если вращается непрерывная кривая 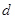 D
D




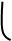
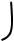

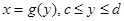 . Тогда:
. Тогда: 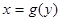








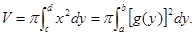
 C
C

 0
0 
 Пример. Найти объём шара радиуса
Пример. Найти объём шара радиуса 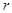 .
. 
Решение. Шар можно рассматривать как тело вращения: полукруг




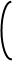
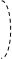 (заштрихован) вращается около оси
(заштрихован) вращается около оси 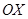 . Полукругограничен другой
. Полукругограничен другой 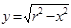

 окружностью
окружностью 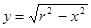 , поэтому:
, поэтому: 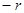

Дата добавления: 2015-10-05; просмотров: 1732;
