Вычисление длины кривой.
 Разделим кривую
Разделим кривую 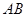 произвольными точками
произвольными точками 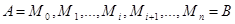 на участки. Соединим соседние точки отрезками прямых. Получим ломаную B
на участки. Соединим соседние точки отрезками прямых. Получим ломаную B
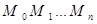 , которую называют вписанной в кривую
, которую называют вписанной в кривую 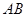 . Её
. Её 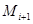
длину будем обозначать 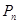 — периметр вписанной ломаной:
— периметр вписанной ломаной: 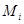
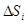
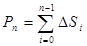 . Длиной кривой
. Длиной кривой 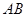 называют конечный предел
называют конечный предел 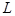 , A
, A
к которому стремится периметр 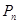 вписанных в неё прямых, когда длина наибольшего из звеньев ломаной
вписанных в неё прямых, когда длина наибольшего из звеньев ломаной 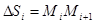 стремится к нулю:
стремится к нулю:



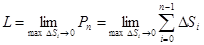
 Получим формулы длины кривой при различном задании этой
Получим формулы длины кривой при различном задании этой


 кривой: в прямоугольных координатах, в параметрической форме
кривой: в прямоугольных координатах, в параметрической форме 
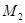
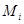
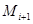
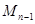 B
B




 и в полярных координатах.
и в полярных координатах. 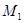
a) Пусть кривая задана в прямоугольных координатах уравнением A

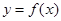 , причём на
, причём на 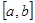
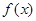 и
и 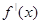 -- непрерывны (кривая 0
-- непрерывны (кривая 0 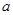
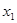
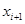
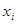
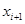
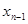
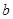
 является графиком функции
является графиком функции 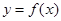 на
на 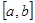 ). Поступим следующим образом: разобьём кривую
). Поступим следующим образом: разобьём кривую



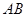 на
на 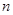 частей точками
частей точками 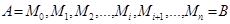 . Пусть точки деления имеют абсциссы
. Пусть точки деления имеют абсциссы 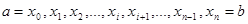 . Соединим соседние точки кривой хордами
. Соединим соседние точки кривой хордами 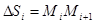 , получим вписанную ломаную, длина которой
, получим вписанную ломаную, длина которой 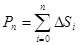 . На каждой
. На каждой 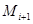
хорде (как на гипотенузе) построим прямоугольный треугольник с 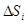
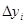


 катетами
катетами 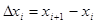 и
и 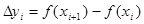 . Тогда длина
. Тогда длина 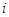 - й
- й 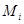
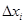

 хорды будет
хорды будет 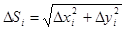 или
или 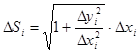 . По формуле
. По формуле 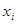
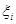
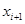

Лагранжа имеем: 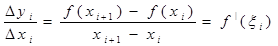 , где
, где 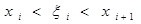 . Тогда
. Тогда 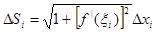 и потому
и потому 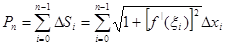 .
.
Перейдём к пределу в этом равенстве при 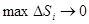 , тогда
, тогда 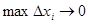 тем более, и потому:
тем более, и потому:
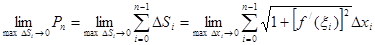
Так как 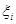 — произвольная точка, то справа стоит предел интегральной суммы для непрерывной функции
— произвольная точка, то справа стоит предел интегральной суммы для непрерывной функции 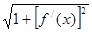 (она непрерывна, т.к. непрерывна по условию
(она непрерывна, т.к. непрерывна по условию 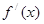 ), а потому этот предел существует и есть определённый интеграл
), а потому этот предел существует и есть определённый интеграл 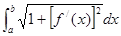 . Слева же стоит предел длин вписанных ломаных, а он равен по определению длине кривой. Таким образом, получаем:
. Слева же стоит предел длин вписанных ломаных, а он равен по определению длине кривой. Таким образом, получаем:
 |

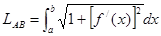 (1)
(1)
(1) короче можно переписать в виде 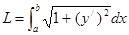
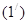 . Так как
. Так как 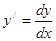 , то
, то
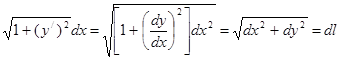 — дифференциал длины дуги.
— дифференциал длины дуги.






 Формулу
Формулу 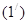 , а , значит, и
, а , значит, и 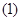 можно записать теперь в виде:
можно записать теперь в виде: 




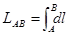 или
или 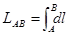 , где А и В – начало и конец кривой АВ. 4 M(2,4)
, где А и В – начало и конец кривой АВ. 4 M(2,4)
 |  |
Пример. Найти длину дуги параболы 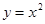 от ( ) О (0,0) до ( ) М (2,4).
от ( ) О (0,0) до ( ) М (2,4).
 Решение:
Решение: 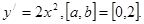 O(0,0) 2
O(0,0) 2 

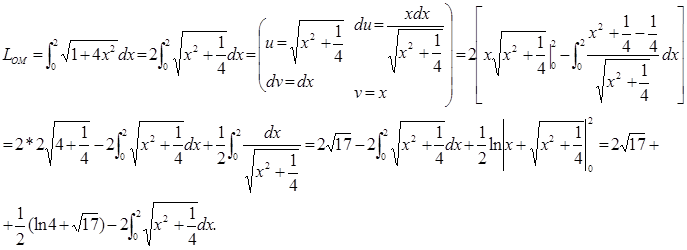 Привели интеграл к «самому себе». Окончательно имеем:
Привели интеграл к «самому себе». Окончательно имеем:
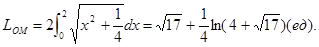
b)  Пусть кривая АВ задана в параметрической форме:
Пусть кривая АВ задана в параметрической форме: 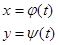 ,
, 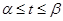 , причём функции
, причём функции 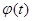 и
и 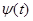 и их производные
и их производные 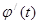 и
и 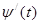 непрерывны на
непрерывны на 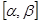 и
и 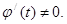 Параметрически заданные функции определяют некоторую функцию
Параметрически заданные функции определяют некоторую функцию 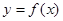 на
на 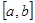 , причём
, причём 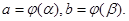 Тогда согласно пункту (1)
Тогда согласно пункту (1) 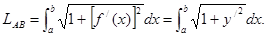



 Cделаем замену переменной в этом интеграле:
Cделаем замену переменной в этом интеграле: 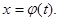 Тогда
Тогда 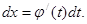 Как известно,
Как известно, 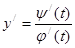 , поэтому
, поэтому 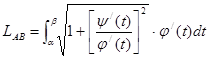 или
или 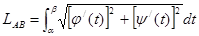 (2)
(2)
Учитывая, что 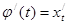 ,
, 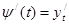 ,
, 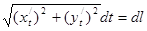 — дифференциал длины дуги в параметрической форме, то формулу (2) снова можно записать:
— дифференциал длины дуги в параметрической форме, то формулу (2) снова можно записать:



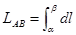
 Пример. Найти длину окружности радиуса
Пример. Найти длину окружности радиуса 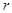 .
.
Решение. Окружность в параметрической форме (центр в начале координат) задастся: 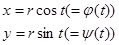 ,
, 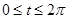 .
.
Тогда 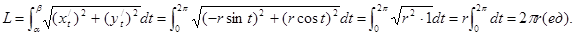
Замечание. Если дана пространственная кривая АВ параметрическими уравнениями:
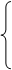
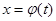 причём функции и их производные непрерывны на
причём функции и их производные непрерывны на 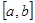 , то длина кривой
, то длина кривой
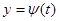 ,
, 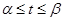 определяется как предел длин вписанных ломаных при
определяется как предел длин вписанных ломаных при 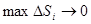 и имеет
и имеет
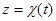 место аналогичная формула:
место аналогичная формула:



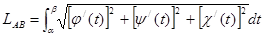 (без доказательства).
(без доказательства).
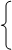
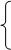
 c) Пусть кривая АВ задана в полярных координатах уравнением
c) Пусть кривая АВ задана в полярных координатах уравнением 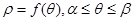 , причём функция
, причём функция 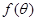 непрерывна на
непрерывна на 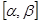 . Сведём задание в полярных координатах к параметрическому, роль параметра играет полярный угол
. Сведём задание в полярных координатах к параметрическому, роль параметра играет полярный угол 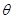 :
: 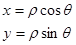 , или
, или 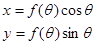 ,
, 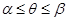 .Тогда
.Тогда 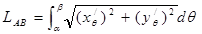 . Имеем:
. Имеем: 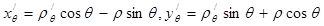 . Тогда
. Тогда
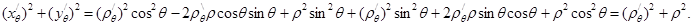 Таким образом,
Таким образом, 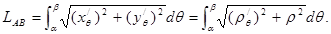 Если писать короче:
Если писать короче: 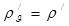 то окончательно получим:
то окончательно получим:



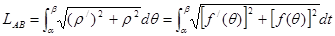 (3)
(3)
 Пример. Вычислить длину первого витка спирали Архимеда:
Пример. Вычислить длину первого витка спирали Архимеда: 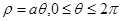 .
.
Решение. 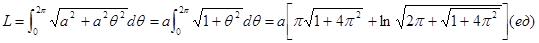 . (Вычислить самостоятельно, интегрируя по частям и приводя интеграл к самому себе).
. (Вычислить самостоятельно, интегрируя по частям и приводя интеграл к самому себе).
§4. Вычисление поверхности тела вращения.



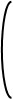 Если вращать кривую АВ:
Если вращать кривую АВ: 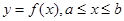 около оси OX, B
около оси OX, B




 то получим поверхность (S) — поверхность вращения.Как A
то получим поверхность (S) — поверхность вращения.Как A

 найти площадь S этой поверхности ? Разобьём
найти площадь S этой поверхности ? Разобьём 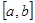 на
на 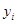
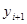
 элементарные точками
элементарные точками 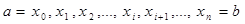 .
. 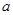
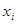
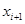
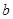

 Проведём через них поперечные сечения. Они разобьют
Проведём через них поперечные сечения. Они разобьют
тело на 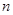 слоёв. Заменим каждый слой усечённым конусом с теми же основаниями и той же высотой
слоёв. Заменим каждый слой усечённым конусом с теми же основаниями и той же высотой 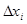 . Радиусы оснований будут
. Радиусы оснований будут 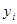 и
и 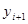 , длина образующей
, длина образующей 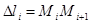 .Тогда боковая поверхность
.Тогда боковая поверхность 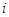 - го конуса будет:
- го конуса будет: 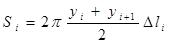 , и поверхность ступенчатой фигуры
, и поверхность ступенчатой фигуры
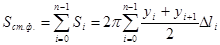 .
.


 Переходя к пределу при
Переходя к пределу при 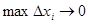 , получим площадь поверхности (S):
, получим площадь поверхности (S):

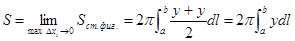 , итак,
, итак, 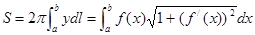
Пример. Вычислить поверхность сферы радиуса 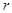 .
.
Решение. Сфера получается вращением полуокружности 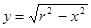 около оси OX. Поэтому имеем:
около оси OX. Поэтому имеем: 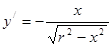 и
и 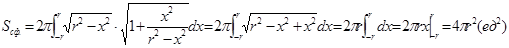
Дата добавления: 2015-10-05; просмотров: 1336;
