Некоторые механические приложения определённого интеграла.

1) Вычисление работы силы.

Пусть материальная точка 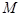под действием силы 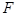перемещается по прямой 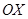из точки 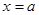в точку 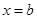. 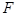направлена в сторону движения. Возможны два случая:

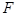а) сила постоянна по величине. Тогда работа силы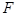

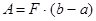(сила на путь);

b) сила 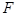изменяется по величине с изменением абсциссы точки 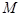, т.е. 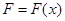— функция от . Будем предполагать, что 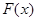непрерывна на 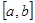.Разобьём 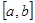на 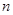элементарных участков с длинами 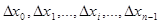. На каждом из них выберем по одной произвольной точке 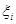и будем считать, что на 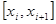сила везде одинакова и равна 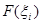. Тогда работа на 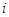- ом участке будет: 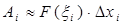и .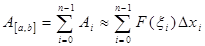

Это приближённое равенство будет тем точнее, чем мельче разбиение 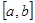на части. Точное равенство получится при 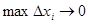. Но справа стоит интегральная сумма для непрерывной функции 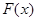, а потому предел существует, и есть определённый интеграл. Таким образом, работа

переменной силы 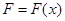на 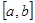находится по формуле:

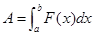
Пример. Какую работу нужно совершить, чтобы тело массы 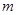поднять с поверхности Земли на высоту ?

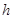Решение. Пусть 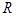— радиус Земли, 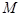- масса Земли. Сила, действующая на тело массы 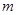равна 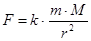, где 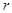— расстояние от центра Земли до тела. Так как при 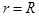имеем ,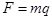

то 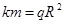, поэтому 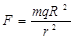. Исполняемая работа:

.

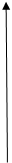
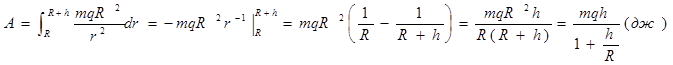2)Вычисление статических моментов и центра масс дуги плоской кривой.

Сначала определим понятие статических моментов и центра масс

системы изолированных точек.

Пусть имеется несколько материальных точек на плоскости

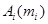
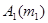
(аналогично и в пространстве) , в которых C

cосредоточены массы 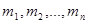и пусть 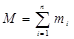суммарная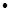 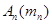0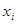

масса всей системы. Статическим моментом материальной точки 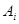относительно оси 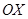называется величина 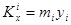, относительно оси 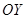величина 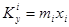. Статическим моментом системы материальных точек относительно осе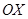й и 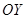соответственно являются суммы: .

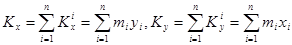Определение.Центром масс системы материальных точек называют такую точку 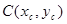, что если в ней сосредоточить всю массу системы 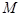, то её статический момент относительно каждой оси равен статическому моменту всей системы относительно этой оси, т.е. .

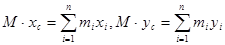Тогда координаты центра масс будут:

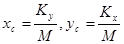
Пусть теперь имеем материальную кривую 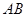с линейной плотностью

материала 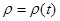. Сама кривая задана параметрическими уравнениями: 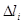B

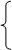
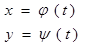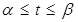, , причём на 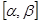сами функции и их A

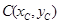
производные 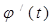и 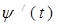непрерывны, функцию плотности 0

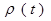тоже предполагаем непрерывной. Разобьём 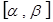на

элементарные части точками .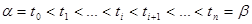

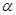
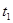
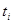
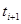
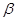
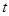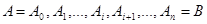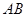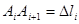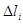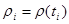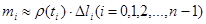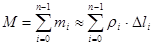Соответствующие этим точки разобьют на элементарные дуги. Будем обозначать длины их .Так как размеры малы, то распределение массы по ней можно считать равномерным и равным, например, .Тогда , и (1).

Статические моменты кривой относительно осей будут:

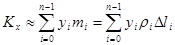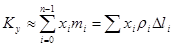(2), (3).

Чем мельче дробление 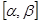, тем мельче дробление 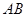, тем точнее эти неравенства. Переходя к пределу при 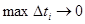в (1) – (3), получим точные равенства:

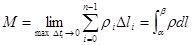В (4) 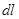означает элемент длины дуги (дифференциал

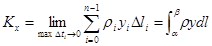(4) длины дуги) 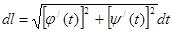. Из (4) находим

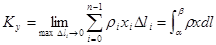. координаты центра масс кривой:

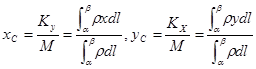(5)

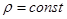В частности, если масса распределена равномерно на , т.е. , то 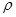выносится за интегралы и сокращается, и из (5) имеем:

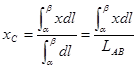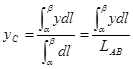, (6)

Если кривая 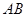задана явным уравнением 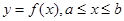, то формулы (5) и (6) остаются в

силе, только .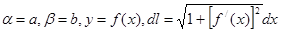

Пример. Найти координаты центра масс верхней части окружности:

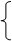
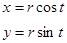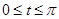, . C

Решение. 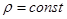. В силу симметрии кривой, сразу ясно, что .

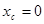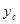Найдём : 0

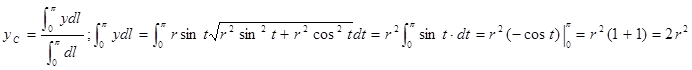
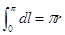. Итак, .

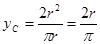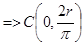
3) Вычисление давления жидкости на погруженную в неё пластину.

Пусть 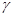— удельный вес жидкости. Плоская пластинка, имеющая 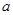A

форму криволинейной трапеции 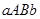, погружена вертикально в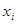

жидкость. Верхняя часть её на глубине 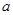, нижняя – на 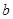. Нужно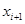

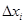
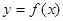
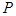найти давление жидкост и на эту пластину. Используем

известный факт: давление жидкости на горизонтальную площадку 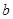B

площади 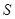, погруженную на глубину 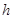, вычисляется по формуле:

.

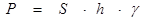Разобьём 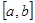на элементарные части длины 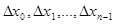. Проведём ординаты точек деления, которые разобьют пластинку на элементарные полосы, которые приближённо можно считать прямоугольниками. Тогда площадь 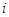— ой полоски будет 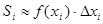. Приближённо можно считать, что вся 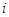— я полоска расположена на одной глубине 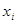, и поэтому давление на неё (на заштрихованную часть) будет 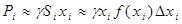. Тогда давление на всю пластинку будет: 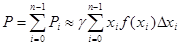. Равенство становится точным при 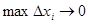. Но этот предел интегральной суммы для непрерывной функции 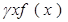на 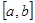, поэтому он существует, и есть определённый интеграл. Таким образом:

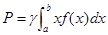или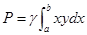

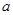
Если пластина ограничена слева кривой ,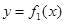

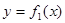
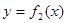
а справа - 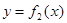, то: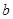

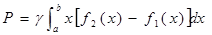
Пример. Найти давление воды на плотину, имеющую форму полукруга радиуса .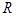

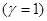Решение. Найдём давление на половину плотины, тогда уравнение границы 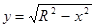, и мы

имеем: 0

.

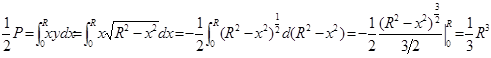R

Тогда всё давление:

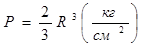
Применяются определённые интегралы и несобственные интегралы для вычисления и многих других величин (моментов инерции, центров масс плоской пластинки и т.п.).