Числовая последовательность
Числовой последовательностью называется функция, определенная на множестве натуральных чисел, которая каждому натуральному числу n ставит в соответствие число 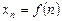 . Числовую последовательность обозначают
. Числовую последовательность обозначают 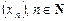 , т. е.
, т. е.
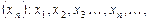
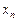 – n-й член последовательности, а формула
– n-й член последовательности, а формула 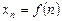 называется формулой общего члена последовательности.
называется формулой общего члена последовательности.
Зная функцию 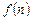 и номер n, можно вычислить любой член последовательности.
и номер n, можно вычислить любой член последовательности.
Последовательность, у которой все члены равны между собой, называется постоянной.
Последовательность может быть задана:
1) аналитическим способом (задается формула n-го члена последовательности, по которому могут быть найдены все остальные);
2) реккурентным способом (задается первый или несколько первых членов последовательности и указывается правило, позволяющее найти последующие члены последовательности через предыдущие);
3) геометрически (точками на числовой оси, соответствующими конкретным значениям n);
4) графическим способом (задаются точки 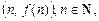 на координатной плоскости);
на координатной плоскости);
5) словеснымописанием;
6) табличным способом.
Последовательность называется возрастающей (строго), если  является возрастающей (строго) числовой функцией, т. е. если
является возрастающей (строго) числовой функцией, т. е. если 
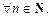
Последовательность называется убывающей (строго), если 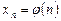 – убывающая (строго) числовая функция, т. е.
– убывающая (строго) числовая функция, т. е. 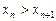
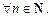
Последовательность 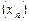 называется неубывающей, если каждый ее член, начиная со второго, не меньше предыдущего, т. е.
называется неубывающей, если каждый ее член, начиная со второго, не меньше предыдущего, т. е. 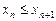
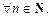
Последовательность (хn) называется невозрастающей, если каждый ее член, начиная со второго, не больше предыдущего, т. е. 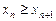
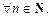
Возрастающая и убывающая последовательности называются монотонными последовательностями.
Последовательность 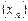 называется ограниченной, если существуют такие числа m и M, что выполняется неравенство
называется ограниченной, если существуют такие числа m и M, что выполняется неравенство 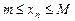
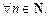
Если существует такое число M, что 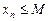
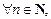 то последовательность называется ограниченной сверху; если существует такое число m, что
то последовательность называется ограниченной сверху; если существует такое число m, что 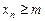
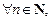 то последовательность называется ограниченной снизу.
то последовательность называется ограниченной снизу.
Последовательность 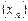 ограничена тогда и только тогда, когда существует такое положительное число C, что выполняется неравенство
ограничена тогда и только тогда, когда существует такое положительное число C, что выполняется неравенство
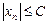
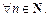
Пример 1. Определить, является ли число 28 членом последовательности 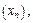 если
если 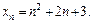
Решение. Число 28 является членом последовательности, если найдется такой номер 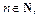 для которого выполняется равенство
для которого выполняется равенство 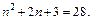 Решим это квадратное уравнение
Решим это квадратное уравнение 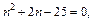 т. е.
т. е. 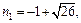
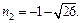 Числа
Числа 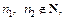 следовательно, число 28 не является членом данной последовательности.
следовательно, число 28 не является членом данной последовательности.
Пример 2. Вычислить первые пять членов последовательности 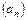 , если
, если 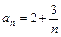 . Определить, для каких членов последовательности
. Определить, для каких членов последовательности 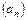 выполняется условие
выполняется условие  .
.
Решение. Подставляя в формулу общего члена значение n = 1, 2, 3, 4, 5, получим:
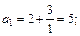
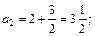
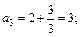
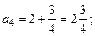
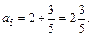
Решим неравенство 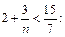
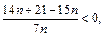
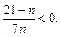
Решением этого неравенства будут 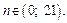 Поэтому, для любых членов последовательности с номерами от 1 до 20 включительно выполняется условие
Поэтому, для любых членов последовательности с номерами от 1 до 20 включительно выполняется условие 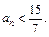
Пример 3. Последовательность задана следующим образом (реккурентно): 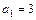 и
и 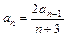 . Вычислить первые четыре ее члена.
. Вычислить первые четыре ее члена.
Решение. Первый член последовательности известен: 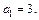 Для вычисления
Для вычисления 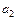 в заданной формуле для
в заданной формуле для 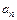 положим
положим 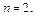 Получим:
Получим:
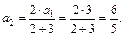
Для вычисления 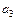 в формуле
в формуле 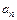 выбираем
выбираем 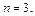 Тогда
Тогда 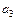 выразится через найденный член
выразится через найденный член 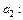

Аналогично:
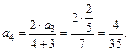
Пример 4.Последовательность 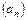 задана формулой общего члена:
задана формулой общего члена: 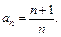 Задать таблично первые восемь ее членов, изобразить их геометрически и графически.
Задать таблично первые восемь ее членов, изобразить их геометрически и графически.
Решение. Вычислим первые восемь членов заданной последовательности и заполним таблицу:
| n | ||||||||
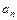
| 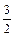
| 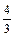
| 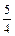
| 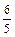
| 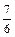
| 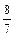
| 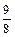
|
Для геометрической иллюстрации изобразим на числовой оси члены последовательности (рис. 10.1).
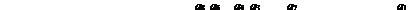
Рис. 10.1
В системе координат 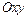 укажем точки плоскости, которые имеют координаты
укажем точки плоскости, которые имеют координаты 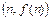 для
для 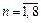 (рис. 10.2).
(рис. 10.2).

Рис. 10.2
Пример 5. Доказать, что последовательность 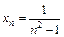 является строго убывающей.
является строго убывающей.
Решение. Если последовательность строго убывающая, то выполняется неравенство 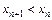 или
или 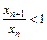
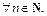
Вычисляем:
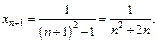
Составим отношение:
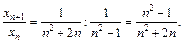
Поскольку 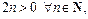 то верно неравенство
то верно неравенство
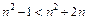
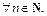
Получаем 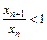 для любых натуральных n.
для любых натуральных n.
Значит, последовательность является строго убывающей.
Пример 6. Исследовать последовательность 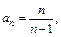
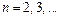 на ограниченность.
на ограниченность.
Решение. Запишем формулу общего члена последовательности следующим образом:
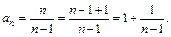
Так как 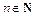 и
и 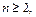 то
то  а поэтому
а поэтому
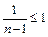 и
и 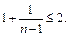
Следовательно, последовательность является ограниченной сверху.
Поскольку неравенство 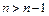 выполняется для всех
выполняется для всех 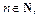
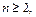 то
то 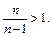
Значит, последовательность является также ограниченной снизу.
Приходим к выводу, что 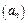 – ограниченная последовательность.
– ограниченная последовательность.
Дата добавления: 2015-09-29; просмотров: 3996;
