Первый и второй замечательные пределы
При вычислении пределов часто используются первый и второй замечательные пределы.
Первый замечательный предел:
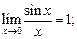 (10.9)
(10.9)
Если 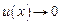 при
при 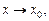 то верна более общая формула первого замечательного предела:
то верна более общая формула первого замечательного предела:
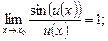 (10.10)
(10.10)
Первый замечательный предел позволяет устранить неопределенность типа 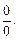
Второй замечательный предел:
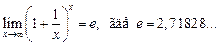 (10.11)
(10.11)
или
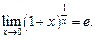 (10.12)
(10.12)
Если 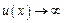 при
при 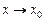
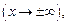 то обобщением формулы (10.11) является формула
то обобщением формулы (10.11) является формула
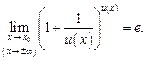 (10.13)
(10.13)
Если 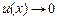 при
при 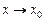
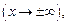 то обобщением формулы (10.12) является формула
то обобщением формулы (10.12) является формула
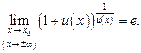 (10.14)
(10.14)
Второй замечательный предел позволяет устранить неопределенность типа 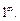
Для того чтобы использовать, например, формулу (10.13), необходимо быть уверенным, что реализованы следующие пять условий (акцентируем их подчеркиванием):
1) 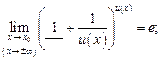 2)
2) 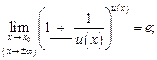
3) 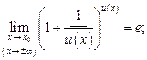 4)
4) 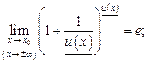
5) 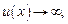 при
при 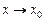
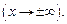
Эти условия достигаются тождественным преобразованием выражения, стоящего под знаком предела.
Пример 1. Вычислить предел функции:
1) 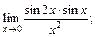 2)
2) 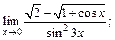
3) 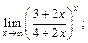 4)
4) 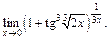
Решение.1) Преобразуем выражение, стоящее под знаком предела:
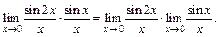
Последний предел, согласно формуле (10.9), равен 1.
Так как при 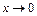 выражение 2х также стремится к нулю, то, умножая числитель и знаменатель на 2 и используя первый замечательный предел, получим:
выражение 2х также стремится к нулю, то, умножая числитель и знаменатель на 2 и используя первый замечательный предел, получим:
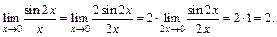
Следовательно, 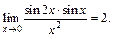
2) При непосредственном вычислении предела получаем неопределенность типа 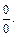
Умножим числитель и знаменатель исходного выражения на 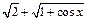 и преобразуем его к виду, когда можно использовать первый замечательный предел (формула (10.10)):
и преобразуем его к виду, когда можно использовать первый замечательный предел (формула (10.10)):
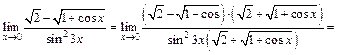
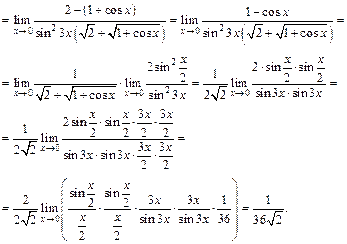
3) Выделим целую часть в основании степени:
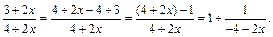
Так как при 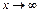 исходное выражение представляет собой неопределенность типа
исходное выражение представляет собой неопределенность типа 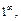 то, используя второй замечательный предел (формула (10.13)), имеем:
то, используя второй замечательный предел (формула (10.13)), имеем:
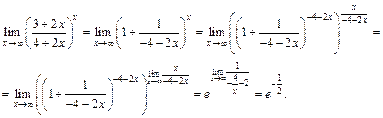
4) В данном случае получаем неопределенность вида 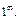 Преобразуем функцию так, чтобы использовать второй замечательный предел (формула (10.14)). Получим:
Преобразуем функцию так, чтобы использовать второй замечательный предел (формула (10.14)). Получим:
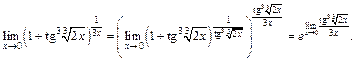
Для вычисления 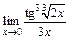 применим первый замечательный предел:
применим первый замечательный предел:
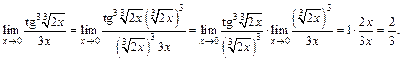
Таким образом, получаем ответ: 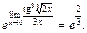
Дата добавления: 2015-09-29; просмотров: 1252;
