Предел функции

Рассмотрим функцию 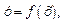определенную в некоторой окрестности точки 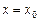(в самой точке 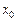данная функция может быть не определена).

Число А называется пределом функции 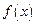в точке 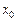(по Гейне), если для любой последовательности (x_n), сходящейся к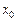 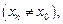последовательность 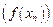соответствующих значений функции сходится к А.

Обозначают:

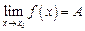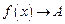или при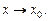

Если функция 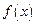в точке 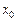имеет предел, то он единственный.

Если функци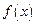и и 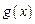имеют пределы в точке 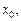то справедливы формулы:

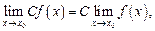где С = const; (10.3)

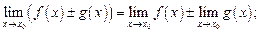(10.4)

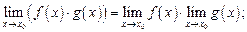(10.5)

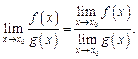(10.6)

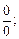
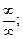
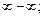
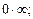
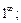
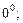
Если непосредственное вычисление предела по формулам (10.3)–(10.6) приводит к неопределенности типа 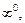то необходимо вначале тождественно преобразовать выражение, стоящее под знаком предела.

Для всех элементарных функций в любой точке их области определения имеет место равенство

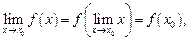(10.7)

которое означает, что операции вычисления предела и функции переставимы.

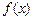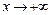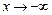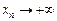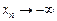Кроме предела функции в точке рассматривают предел функции на бесконечности: число A называется пределом функции при (или ), если для всякой последовательности (x_n), (или ) при 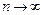последовательность 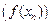соответствующих значений функции сходится к числу A.

Обозначают:

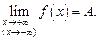
Для предела функции на бесконечности также справедливы формулы (10.3)–(10.6).

Функция 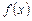называется бесконечно малой функцией при 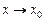(или 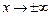), если

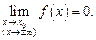
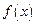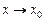
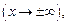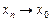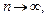
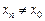Функция называется бесконечно большой при если для всякой последовательности (x_n), при (или 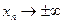) последовательность соответствующих значений функции 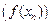является бесконечно большой.

Обозначают:

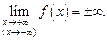(10.8)

Если 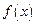– бесконечно большая функция при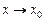 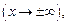то она не имеет предела (предел – это число!). Запись формулы (10.8) следует воспринимать лишь как обозначение бесконечно большой функции.

Пример 1. Пользуясь определением предела функции по Гейне, доказать, что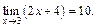

Решение. Пусть (x_n) – произвольная последовательность, которая сходится к 3 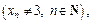т. е.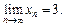

Тогда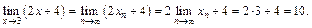

Пример 2. Вычислить предел функции в точке:

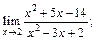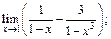1) 2) 3)

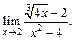
Решение. 1) При непосредственном использовании формул (10.3)–(10.6) получаем неопределенность вида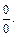

Разложим числитель и знаменатель на множители и сократим дробь на общий множитель. Получим:

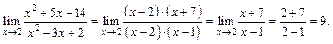
2) Непосредственное вычисление приводит к неопределенности типа 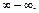Для раскрытия приведем выражение в скобках к общему знаменателю:

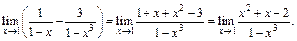
Далее разлагаем числитель и знаменатель на множители. Получаем:

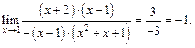
3) Непосредственное вычисление предела при 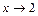приводит к неопределенности типа 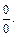Умножим числитель и знаменатель на неполный квадрат суммы выражений 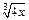и 2, чтобы в числителе получить разность кубов:

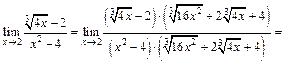
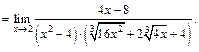
Поскольку неопределенность типа 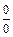сохранилась, разложим многочлены на множители и сократим:

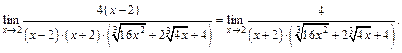
Переход к пределу при 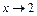дает:

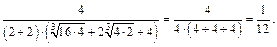
Пример 3. С помощью вычислений определить, является ли функция 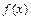бесконечно малой или бесконечно большой при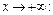

1) 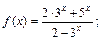2)

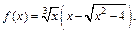
Решение. 1) Чтобы ответить на вопрос задачи, необходимо рассмотреть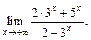

Непосредственное вычисление этого предела приводит к неопределенности типа 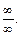Вынесем в числителе и знаменателе старшее основание, т. е. 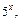за скобки:

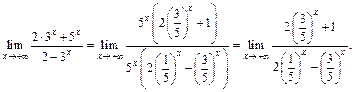
Так как показательная функция 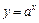при 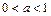является убывающей, то при 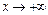получим:

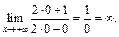
Тогда, согласно определению, функция 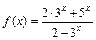является бесконечно большой.

2) Вычислим 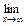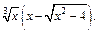При 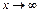выражение в скобках представляет собой разность двух бесконечно больших величин 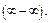Умножив и разделив функцию на выражение 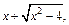получим:

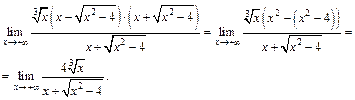
В результате преобразований возникла неопределенность типа 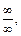а поэтому разделим числитель и знаменатель на старшую степень, т. е. на x. Получим:

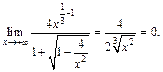
Следовательно, по определению функция 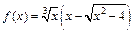является бесконечно малой.