Параметры параболы

Точка F(p/2, 0) называется фокусомпараболы, величина p – параметром, точка О(0, 0) – вершиной (рис. 9.15). При этом прямая OF, относительно которой парабола симметрична, задает ось этой кривой.

Рис. 9.15

Величина 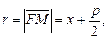где M(x, y) – произвольная точка параболы, называется фокальным радиусом, прямая D: x = –p/2 – директрисой (она не пересекает внутреннюю область параболы). Величина 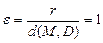называется эксцентриситетомпараболы.

Основное характеристическое свойство параболы: все точки параболы равноудалены от директрисы и фокуса (рис. 9.15).

Существуют иные формы канонического уравнения параболы, которые определяют другие направления ее ветвей в системе координат (рис. 9.16):

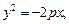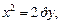а) б) в)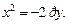

Рис. 9.16

Для параметрического задания параболы в качестве параметра t может быть взята величина ординаты точки параболы:

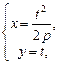
где t – произвольное действительное число.

Пример 1.Определить параметры и форму параболы по ее каноническому уравнению:

1) 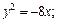2)

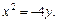
Решение.1) Уравнение y² = –8x определяет параболу с вершиной в точке О(0; 0), симметричную относительно оси Оx. Ее ветви направлены влево. Сравнивая данное уравнение с уравнением y²= –2px, находим: 2p = 8, p = 4, p/2 = 2. Следовательно, фокус находится в точке F(–2; 0), уравнение директрисы D: x = 2 (рис. 9.17).

Рис. 9.17

2) Уравнение x² = –4y задает параболу с вершиной в точке O(0; 0), симметричную относительно оси Oy. Ее ветви направлены вниз. Сравнивая данное уравнение с уравнением x² = –2py, находим: 2p = 4, p = 2, p/2 = 1. Следовательно, фокус находится в точке F(0; –1), уравнение директрисы D: y = 1 (рис. 9.18).

Рис. 9.18

Пример 2.Определить параметры и вид кривой x² + 8x – 16y – 32 = 0. Сделать рисунок.

Решение. Преобразуем левую часть уравнения, используя метод выделения полного квадрата:

x² + 8x – 16y – 32 = 0;

(x + 4)² – 16 – 16y – 32 = 0;

(x + 4)² – 16y – 48 = 0;

(x + 4)² – 16(y + 3) = 0.

В результате получим:

(x + 4)² = 16(y + 3).

Это каноническое уравнение параболы с вершиной в точке (–4; –3), параметром p = 8, ветвями, направленными вверх 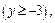осью x = –4. Фокус находится в точке F(–4; –3 + p/2), т. е. F(–4; 1) Директриса D задается уравнением y = –3 – p/2 или y = –7 (рис. 9.19).

Рис. 9.19

Пример 3. Написать уравнение кривой, все точки которой равноудалены от прямой y = –3 и точки F(0; 3).

Решение. Точка F(0; 3) лежит на оси Oy и находится с прямой y = –3 по разные стороны от начала координат, причем на одинаковом расстоянии (d = 3). Это позволяет заключить, что искомой кривой является парабола x² = 2py с параметром p = 2 × 3 = 6, т. е. x² = 12y (рис. 9.20).

Рис. 9.20

Пример 4.Составить уравнение параболы с вершиной в точке V(3; –2) и фокусом в точке F(1; –2).

Решение. Вершина и фокус данной параболы лежат на прямой, параллельной оси Ox (одинаковые ординаты), ветви параболы направлены влево (абсцисса фокуса меньше абсциссы вершины), расстояние от фокуса до вершины равно p/2 = 3 – 1 = 2, p = 4. Следовательно, искомое уравнение

(y + 2)² = –2 · 4(x – 3) или (y + 2)² = –8(x – 3).