Производная функции
Понятие производной. Правила
Дифференцирования. Таблица производных
Пусть функция 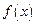 определена в точке
определена в точке 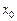 и в некоторой ее окрестности, x – точка из рассматриваемой окрестности. Приращением аргументав точке
и в некоторой ее окрестности, x – точка из рассматриваемой окрестности. Приращением аргументав точке 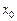 называется величина
называется величина 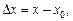 приращением функции – величина
приращением функции – величина 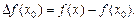 Если выразить
Если выразить  то
то 
Производной функции 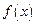 в точке
в точке 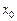 называется предел отношения приращения функции к приращению аргумента, когда последнее стремится к нулю, при условии, что предел существует.
называется предел отношения приращения функции к приращению аргумента, когда последнее стремится к нулю, при условии, что предел существует.
Производную в точке обозначают 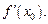 По определению
По определению
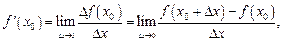 (11.1)
(11.1)
или, что то же,
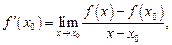 (11.2)
(11.2)
при условии, что пределы (11.1) и (11.2) существуют.
Функция, имеющая производную в точке, называется дифференцируемой в этой точке. Операция нахождения производной называется дифференцированием.
Производная функции в точке – это число. Если функция дифференцируема на некотором множестве X из ее области определения, то  также является функцией (ее обозначают также
также является функцией (ее обозначают также 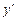 ).
).
Дата добавления: 2015-09-29; просмотров: 759;
