Основные правила дифференцирования. Пусть – дифференцируемые функции
Пусть 
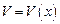 – дифференцируемые функции. Справедливы формулы:
– дифференцируемые функции. Справедливы формулы:
 где
где 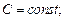 (11.3)
(11.3)
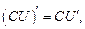 где
где 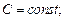 (11.4)
(11.4)
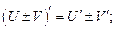 (11.5)
(11.5)
 (11.6)
(11.6)
 (11.7)
(11.7)
Таблица производных основных элементарных функций
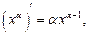 где
где  в частности:
в частности:
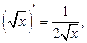
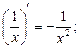
 где
где 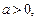
 в частности,
в частности, 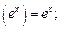
 где
где 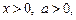
 в частности
в частности 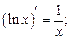
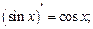
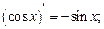
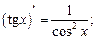
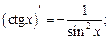



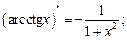


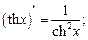
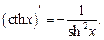
Пример 1. Найти производную функции 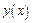 в точке
в точке 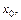 пользуясь определением, если:
пользуясь определением, если:
1) 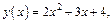
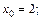 2)
2) 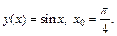
Решение. 1) Используем определение производной в виде формулы (11.1):

Поскольку по условию  то
то 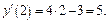
2) По формуле (11.1) получаем:

Далее, применив тригонометрическую формулу
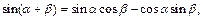
получим:

Так как при 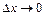 имеем
имеем  и, применив формулу первого замечательного предела, получаем:
и, применив формулу первого замечательного предела, получаем:

Поскольку по условию 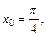 то
то 
Пример 2.Вычислить производную функции 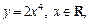 пользуясь определением производной.
пользуясь определением производной.
Решение. Пусть x – произвольная фиксированная точка из  Пользуясь формулой (11.1), имеем:
Пользуясь формулой (11.1), имеем:
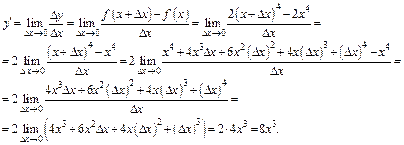
Таким образом, операция дифференцирования ставит в соответствие функции 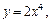
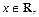 функцию
функцию 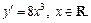
Пример 3.Найти производную функции:
1) 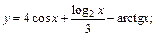 2)
2) 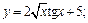 3)
3) 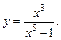
Решение. 1) Дифференцируем функцию и используем формулы (11.4), (11.5) и таблицу производных, получаем:

2) Дифференцируем функцию по формулам (11.3)–(11.6) и соответствующим формулам таблицы производных:

3) Дифференцируем функцию по формулам (11.7), (11.5), (11.3) и первой формуле таблицы производных:
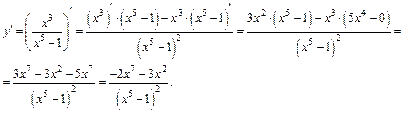
Пример 4. Вычислить производную функции, используя правила дифференцирования и таблицу производных:
1) 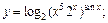 2)
2) 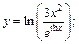
3) 
Решение.1) Преобразуем функцию, пользуясь свойствами логарифма:

Полученное выражение дифференцируем по формулам (11.4)–(11.6) и формулам таблицы производных:
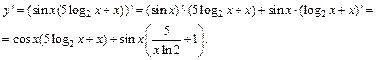
2) Перед дифференцированием преобразуем выражение, пользуясь свойствами логарифма:
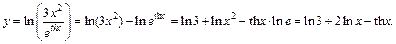
Дальше воспользуемся формулами (11.3)–(11.5) и таблицей производных:
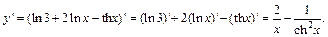
3) Так как непосредственное дифференцирование вызывает значительные трудности, предварительно упростим выражение по формулам тригонометрии:

Полученное выражение дифференцируем по формуле (11.7) и соответствующим формулам таблицы производных:

Дата добавления: 2015-09-29; просмотров: 809;
