Если последовательность имеет предел, то этот предел единственный.

Если последовательность 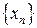имеет предел, равный 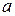, то говорят, что эта последовательность сходится к 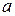. Например, поскольку 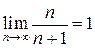, то говорят, что последовательность 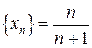сходится к 1.

Последовательность, не имеющая предела, называется расходящейся. Например, последовательность 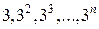,… не имеет предела, значит она расходится.

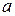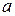Геометрическая интерпретация предела. Постоянное число называется пределомпеременной , если для любой окрестности с центром в точке , даже сколь угодно малого радиуса 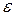, найдется такое значение , что точки, изображающие это значение и все последующие значения переменной , попадут в эту окрестность (рис.1). Обратим внимание на то, что вне любой окрестности точки 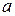лежит лишь конечное число значений переменной .

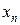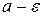
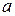
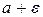
0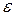

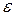
Рис. 1 Геометрическая интерпретация предела последовательности