Бесконечно малые и бесконечно большие функции
Функция 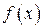 называется бесконечно малой при
называется бесконечно малой при 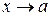 , если
, если
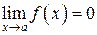 .
.
Функция называется бесконечно большой при 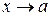 , если для всех значений
, если для всех значений  из некоторой окрестности точки
из некоторой окрестности точки 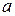 выполняется неравенство
выполняется неравенство 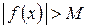 , где
, где 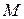 – любое положительное число, даже сколь угодно большое. В этом случае пишут:
– любое положительное число, даже сколь угодно большое. В этом случае пишут:
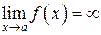 .
.
Функция 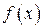 называется ограниченной при
называется ограниченной при 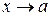 , если существует такое положительное число
, если существует такое положительное число 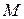 , что для всех значений
, что для всех значений  из окрестности числа
из окрестности числа 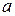 выполняется неравенство
выполняется неравенство 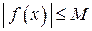 .
.
Связь между бесконечно большими и
бесконечно малыми функциями:
§ Если 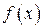 при
при 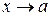 – бесконечно большая функция, то функция
– бесконечно большая функция, то функция 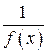 бесконечно малая (условно:
бесконечно малая (условно: 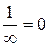 ).
).
§ Если при 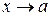 функция
функция 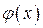 бесконечно малая, то функция
бесконечно малая, то функция 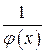 – бесконечно большая, причем предполагается, что в окрестности точки
– бесконечно большая, причем предполагается, что в окрестности точки 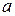 функция
функция 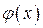 в нуль не обращается (условно :
в нуль не обращается (условно : 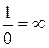 ).
).
Дата добавления: 2015-09-28; просмотров: 900;
