Раскрытие неопределенностей
При нахождении предела функции нужно в выражении функции заменить аргумент его предельным значением. Если при этом не возникает трудностей (неопределенностей различных видов), то предел вычисляется легко. Например
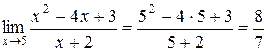 .
.
Однако, не всегда удается простой подстановкой вычислить предел. Рассмотрим некоторые приемы отыскания пределов в случае неопределенностей.
Неопределенность вида 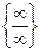 ,порожденную отношением многочленов, раскрывают делением числителя и знаменателя на аргумент в наибольшей степени дроби.
,порожденную отношением многочленов, раскрывают делением числителя и знаменателя на аргумент в наибольшей степени дроби.
Пример. Найти
1)  . 2)
. 2) 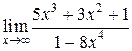 . 3)
. 3) 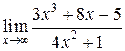 .
.
Решение.
При 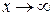 и числитель, и знаменатель дроби бесконечно большие. Значит имеем дело с отношением двух бесконечно больших функций. Для решения задачи следует разделить числитель и знаменатель на
и числитель, и знаменатель дроби бесконечно большие. Значит имеем дело с отношением двух бесконечно больших функций. Для решения задачи следует разделить числитель и знаменатель на  в высшей степени (в данном случае на
в высшей степени (в данном случае на 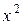 ), а после перейти к непосредственному вычислению предела. Итак
), а после перейти к непосредственному вычислению предела. Итак
1) 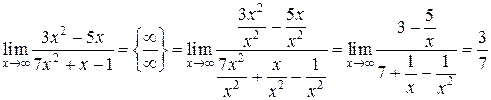
(величины  при
при 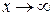 являются бесконечно малыми величинами, поэтому
являются бесконечно малыми величинами, поэтому  ).
).
В данном примере степень числителя равна степени знаменателя.
2) 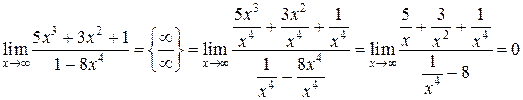
В данном примере степень числителя меньше степени знаменателя.
3) 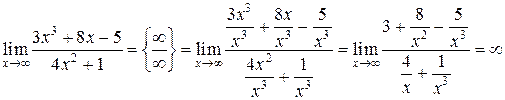
В данном примере степень числителя больше степени знаменателя.
Правило раскрытия неопределенности вида 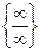
1) если степень числителя больше степени знаменателя, то предел равен 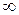 ;
;
2) если степень числителя равна степени знаменателя, то предел равен отношению коэффициентов при старших степенях в числителе и знаменателе;
3) если степень числителя меньше степени знаменателя, то предел равен 0.
Неопределенность вида 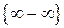 ,порожденную разностью двух бесконечно больших величин одного знака, раскрывают домножением на сопряженное выражение, приведением к общему знаменателю или вынесением общего множителя. При домножении на сопряженное выражение следует одновременно разделить на него.
,порожденную разностью двух бесконечно больших величин одного знака, раскрывают домножением на сопряженное выражение, приведением к общему знаменателю или вынесением общего множителя. При домножении на сопряженное выражение следует одновременно разделить на него.
Пример. Найти
1) 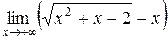 . 2)
. 2) 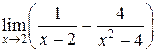
Решение.
1) Умножим и разделим выражение, стоящее под знаком предела, на сопряженное:

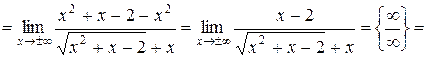
 .
.
2) Приводим к общему знаменателю и преобразуем
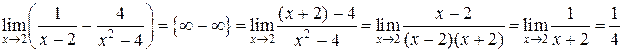 .
.
Неопределенность вида 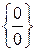 при
при 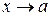 , порожденную отношением двух многочленов, раскрывают выделением в числителе и знаменателе множителя
, порожденную отношением двух многочленов, раскрывают выделением в числителе и знаменателе множителя 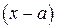 и сокращением на него.
и сокращением на него.
Для раскрытия неопределенности 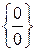 , содержащей иррациональные выражения, следует числитель и знаменатель домножить на сопряженное выражение для иррационального, после чего сделать необходимые упрощения и вычислить предел.
, содержащей иррациональные выражения, следует числитель и знаменатель домножить на сопряженное выражение для иррационального, после чего сделать необходимые упрощения и вычислить предел.
Пример. Найти
1) 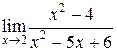 . 2)
. 2) 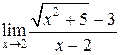 .
.
Решение.
1) Разложим числитель и знаменатель на множители:
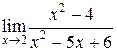
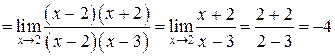 .
.
2) Перенесем иррациональность в знаменатель, для чего умножим числитель и знаменатель на выражение, сопряженное числителю, ( 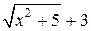 ) и получим:
) и получим:
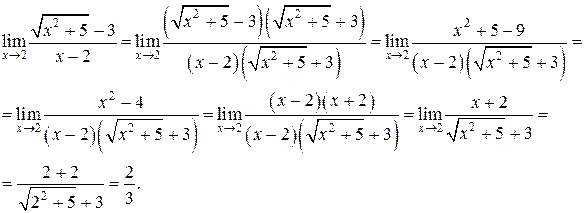
Дата добавления: 2015-09-28; просмотров: 1780;
