Предел функции. Определение. Число является пределом функции при , если для любого, даже сколь угодно малого
| Определение. | Число 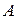 является пределом функции является пределом функции 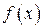 при при 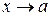 , если для любого, даже сколь угодно малого, положительного числа , если для любого, даже сколь угодно малого, положительного числа 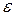 существует такое положительное число существует такое положительное число  , что для всех , что для всех  , удовлетворяющих условию , удовлетворяющих условию 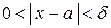 , выполняется неравенство , выполняется неравенство
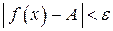 . .
|
Тот факт, что функция 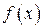 при
при 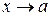 имеет предел, равный
имеет предел, равный 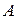 , символически обозначают в виде
, символически обозначают в виде
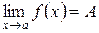 .
.
Геометрическая интерпретация. Пусть дан график функции 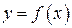 , имеющей предел при
, имеющей предел при 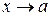 , равный
, равный 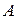 (рис.2).
(рис.2).
Для каждого наперед заданного значения 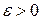 , найдется окрестность точки
, найдется окрестность точки 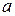 радиуса
радиуса  , такая, что часть графика данной функции, соответствующая окрестности
, такая, что часть графика данной функции, соответствующая окрестности 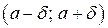 , содержится внутри полосы, ограниченной прямыми
, содержится внутри полосы, ограниченной прямыми 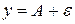 ,
, 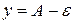 .
.

| 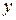
| |||||||||||||||||||||||||
| ||||||||||||||||||||||||||
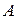
| 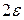
| 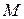
| ||||||||||||||||||||||||
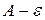
| ||||||||||||||||||||||||||
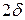
| ||||||||||||||||||||||||||
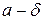
| 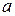
| 
| 
|
Рис. 2 Геометрическая интерпретация предела функции
Дата добавления: 2015-09-28; просмотров: 778;
