Свойства пределов
Пусть функции 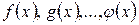 имеют пределы при
имеют пределы при 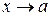 . Тогда
. Тогда
1. Предел постоянной равен самой этой постоянной
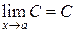 .
.
2. Постоянный множитель можно выносить за знак предела
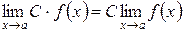 .
.
3. Предел алгебраической суммы конечного числа функций равен сумме пределов функций, если эти пределы существуют
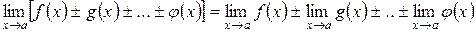 .
.
4. Предел произведения конечного числа функций равен произведению пределов этих функций, если эти пределы существуют
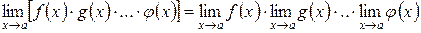 .
.
5. Предел частного двух функций равен частному их пределов, если 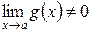
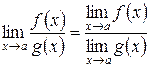 .
.
6. Предел степени равен пределу основания в степени предела показателя степени
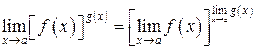 .
.
7. Предел логарифма равен логарифму предела 
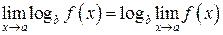 .
.
Дата добавления: 2015-09-28; просмотров: 3437;
