Интегральная формула Муавра – Лапласа
Для того, чтобы определить вероятность попадания числа m (появления события A в схеме Бернулли при большом числе испытаний n) в заданный промежуток [а,в]: 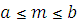 , можно использовать интегральную формулу Муавра – Лапласа:
, можно использовать интегральную формулу Муавра – Лапласа:
| |
где
– функция Лапласа, значения которой находятся по таблицам.
Для относительной частоты (частости) m/n появления события A в n испытаниях Бернулли справедлива приближенная формула
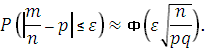
Для числа m появлений события A справедлива приближенная формула
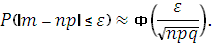
Примеры:
______________________________________________________
1. В партии из 768 арбузов каждый арбуз оказывается неспелым с вероятностью q = 0,25. Найти вероятность того, что количество спелых арбузов будет находиться в пределах от 560 до 600.
Из условия задачи имеем n=768 испытаний Бернулли с вероятностью найти зрелый арбуз, равной р=0,75. Если m – число удачных выборов, то требуется найти вероятность 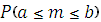 , где a = 560, b = 600.
, где a = 560, b = 600.
Поскольку
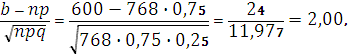
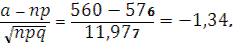
то по интегральной формуле Муавра – Лапласа получим:
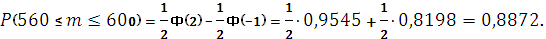
2. Сколько нужно произвести бросаний монеты, чтобы с вероятностью 0,99 можно было утверждать, что относительная частота выпадения герба отличается от 0,5 по модулю не более чем на 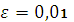 ?
?
По формуле 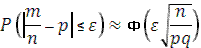 , в которой
, в которой 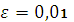 , имеем:
, имеем:
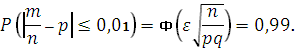
По таблицам значений функции Лапласа находим, что
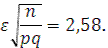
Откуда выражаем п и, подставляя p=0,5; q=0,5, получим:
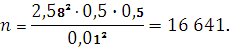
________________________________________________________________
Дата добавления: 2015-09-28; просмотров: 2394;
