Случайные величины. Закон распределения случайной величины
Случайной величиной называется величина, которая в результате опыта может принять определенное, но заранее не известное, значение. Дискретной называют случайную величину, возможные значения которой есть отдельные числа, которые можно пронумеровать. Например, число участников испытания, количество положительных тестов в психодиагностике.
Непрерывной называется случайная величина, которая может принимать значения из некоторого бесконечного или конечного промежутка, т.е. возможные значения заполняют непрерывно некоторый промежуток. Например, скорость некоторого объекта, ошибка взвешивания на точных весах и т.д.
Случайные величины обозначаются большими буквами X, Y, Z, а их возможные значения – малыми буквами x, y, z. Запись X= x означает, что случайная величина Х приняла значение х, запись Р(Х=х) означает вероятность того, что Х приняла значение х.
Каждое значение дискретной случайной величины появляется с некоторой вероятностью. Законом распределения случайной величины называется соответствие между значениями случайной величины и их вероятностями. О случайной величине говорят, что она имеет данный закон распределения. Простейшей формой задания закона распределения является таблица, называемая рядом распределения, в которой перечислены возможные значения случайной величины и соответствующие им вероятности (таблица 5.1).
Таблица 5.1
| хi | x1 | x2 | … | xn |
| pi | p1 | p2 | … | pn |
В этой таблице 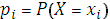 – это вероятность события
– это вероятность события 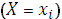 . Так как в каждом испытании случайная величина Х принимает одно и только одно возможное значение, события Х = х1, Х = х2, … Х = хп образуют полную группу, а, значит, сумма вероятностей равна единице:
. Так как в каждом испытании случайная величина Х принимает одно и только одно возможное значение, события Х = х1, Х = х2, … Х = хп образуют полную группу, а, значит, сумма вероятностей равна единице:
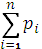 =1.
=1.
Пример:
_________________________________________________________
Всхожесть семян данного растения определяется вероятностью 0,6. Пусть X – случайная величина – число появившихся растений из 5 семян. Найти закон распределения X.
Случайная величина X может принимать значения 0, 1, 2, 3, 4 ,5. Вероятности, соответствующие этим значениям случайной величины – 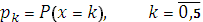 . Вычислим эти вероятности. Можно считать, что имеется схема n = 5 испытаний Бернулли с вероятностью успешного результата p = 0,6. Тогда по формуле Бернулли
. Вычислим эти вероятности. Можно считать, что имеется схема n = 5 испытаний Бернулли с вероятностью успешного результата p = 0,6. Тогда по формуле Бернулли 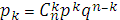 . При n = 5, p = 0,6, q = 0,4 находим:
. При n = 5, p = 0,6, q = 0,4 находим: 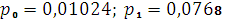 ;
; 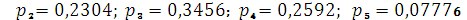 .
.
Таким образом, получаем закон распределения случайной величины X:
| хi | 0 | 1 | 2 | 3 | 4 | 5 |
| pi | 0,01024 | 0,0768 | 0,2304 | 0,3456 | 0,2592 | 0,07776 |
Можно проверить, что =1.
_____________________________________________________________
Дата добавления: 2015-09-28; просмотров: 1612;
