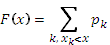Функция распределения случайной величины. Ее свойства
Другой формой закона распределения случайной величины является функция распределения F(x), представляющая собой вероятность того, что случайная величина Х примет значение, меньшее х, т.е.
F(x) = Р(Х 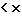 )
)
Функцию распределения иногда называют интегральной функцией распределения.
Для дискретной случайной величины X с законом распределения 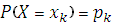 , k = 1, 2, …, функция распределения имеет вид
, k = 1, 2, …, функция распределения имеет вид
|
,
где символ xk 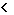 x означает, что суммируются вероятности тех значений, которые меньше х.
x означает, что суммируются вероятности тех значений, которые меньше х.
Графиком функции распределения дискретной случайной величины является график кусочно-постоянной функции. Скачки функции 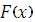 в точках разрыва
в точках разрыва 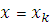 равны вероятностям этих значений
равны вероятностям этих значений 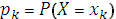 . Cумма всех скачков равна 1.
. Cумма всех скачков равна 1.
Пример:
_______________________________________________ _____________
Построить график функции распределения для случайной величины предыдущего примера.
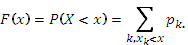
При 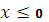 , очевидно,
, очевидно, 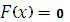 ;
;
при 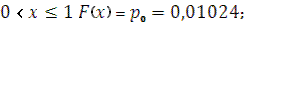
при 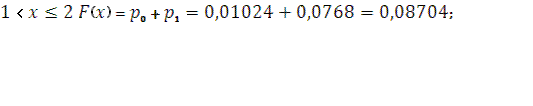
при 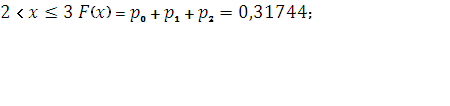
при 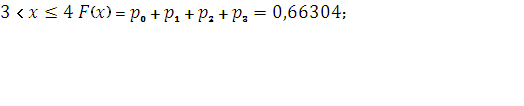
при 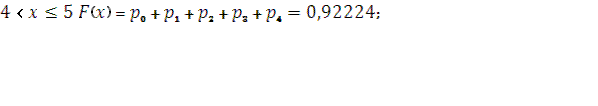
при 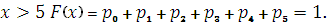
График функции распределения 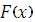 изображен на рис. 5.2.
изображен на рис. 5.2.
 F(x)
F(x)

 1
1

 0,6
0,6






 0 1 2 3 4 5 x
0 1 2 3 4 5 x
Рис. 5.2
Функция распределения любой случайной величины обладает следующими свойствами:
1. Множество значений функции находится на отрезке [0; 1]:
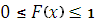 .
.
2. Функция 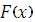 не убывает, т.е. если х2
не убывает, т.е. если х2 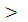 х1, то
х1, то  .
.
3. Если все возможные значения случайной величины принадлежат интервалу (а; в), то 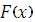 =0 при х
=0 при х 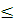 а,
а, 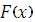 =1 при х
=1 при х 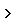 в.
в.
4. Для 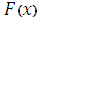 выполняются предельные соотношения:
выполняются предельные соотношения:
5. Функция распределения непрерывна слева.
6. Если х2 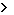 х1, то
х1, то  = Р(х1
= Р(х1 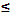 Х
Х 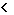 х2).
х2).
В случае, когда х1=а и х2=в, получим: Р(а 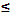 Х
Х 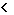 в) =
в) =  –
– 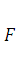 , т.е. вероятность принятия случайной величиной значения на промежутке [а; в) равна приращению функции распределения на этом промежутке.
, т.е. вероятность принятия случайной величиной значения на промежутке [а; в) равна приращению функции распределения на этом промежутке.
Дата добавления: 2015-09-28; просмотров: 675;